Оглавление:

Свободные затухающие колебания
- Свободное демпфирование вибрации Дифференциальное уравнение свободной вибрации в присутствии источника рассеяния
(поглощения) энергии создает сопротивление (R = -a / ‘), пропорциональное скорости, и принимает вид: tu «+ ay ‘+ cy =
0 (10,38) или y «+ 2nu ‘+ ), (10.40). Где n — коэффициент демпфирования Людмила Фирмаль
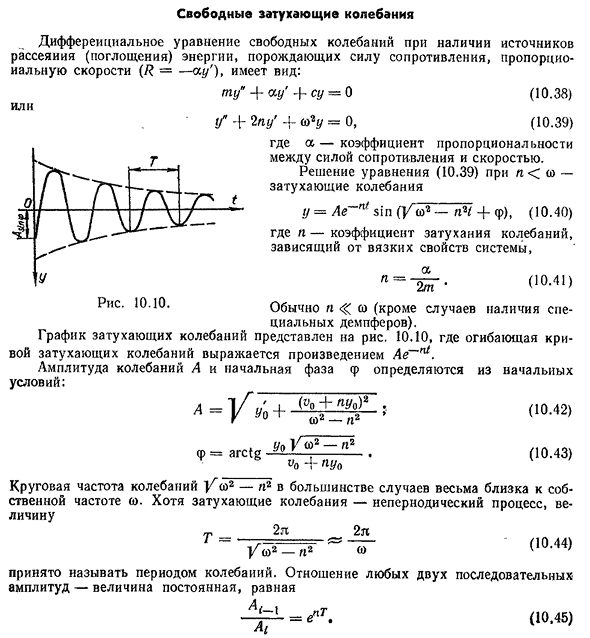
колебаний, зависящий от вязкостных характеристик системы. Обычно n co (кроме специальных амортизаторов). График затухающей вибрации показан на рисунке. В 10.10 огибающая
затухающей кривой колебаний представлена произведением Ae ~ nt. Амплитуда и начальная фаза cf вибрации A определяются из начальных условий. A =] / ^ + — «<1 0 -4 2 * (10.43) sr = arct, g y9 U co2-n2 ;
- , v0-fpu0 В большинстве случаев круговая частота вибрации V co2-u2 очень близка к собственной частоте co. Затухающая вибрация — апериодический процесс, но величина Т-2 р 2 я ~ Y w 2-P 2 CO Это
называется периодом вибрации. Отношение любых двух последовательных амплитуд является одинаковым постоянным значением. L <~ 1 _ L ~ ‘ (10.44) (10.45) Скорость затухания
224 собственных колебаний характеризуется значением 0 = nT = In enТ Людмила Фирмаль
(10,46), которое называется логарифмическим уменьшением вибрации. При сильном демпфировании (n> co) движение приобретает резкие непериодические характеристики.
Смотрите также:
| Колебания упругих систем с одной степенью свободы | Вынужденные колебания линейной системы при сопротивлении, пропорциональном скорости |
| Свободные незатухающие колебания | Расчеты на ударные нагрузки |

