Оглавление:
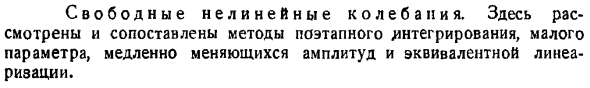







Свободные нелинейные колебания
- Здесь рассматривается и сравнивается метод ступенчатого интегрирования, малых параметров, медленно меняющихся амплитуд и эквивалентной линеаризации. Метод постепенного закрепления стыковка, подгонка удобен в использовании, когда нелинейные дифференциальные уравнения движения интегрируются в отдельные sections. В частности, этот метод рекомендуется применять, когда нелинейные системы линейны на отдельных этапах. Это делается, например, с нелинейными свойствами силы упругости, которая состоит из нескольких соединенных прямых segments. В этом случае можно получить точное решение линейного дифференциального уравнения на отдельной кинетической стадии.
Подгонка этих решений основана на обобщенных координатах в точке пересечения движения и равенстве обобщенной скорости. Метод малых параметров полезен при интегрировании автономного нелинейного дифференциального уравнения вида Л А х р- х Где f x — нелинейная функция от x, а p-малый параметр. Преимущество этого метода заключается в том, что при требуемой степени p, p , p3,… можно найти периодическое решение, вычисленное с точностью до члена, содержащего малый параметр. Требуемый параметр p требуется в виде удлинителя мощности. x x PCT p x p x3…
Движение прекратится в том край-нем положении диска, в котором момент силы трения окажется больше или равным упругому моменту проволоки. Людмила Фирмаль
Где xt, x1, x1 и xa-периодические функции определенной циклической частоты p и нескольких циклических частот, и подлежат следующим определениям 2 требуемой круговой частоты p также описывается в расширении мощности к мощности меньшего параметра p. pg k pax p Oi psa3 4 -… Значение постоянной Xj, ag, o … выбирается таким образом, чтобы в решении уравнения не было бесконечно возрастающего резонансного члена. Метод малых параметров обеспечивает соответствующее приближение к малому числу расширенных членов в периодическом решении, являющемся obtained. It обычно оказывается достаточным для решения задачи вплоть до раздела, содержащего малые параметры 1-го порядка.
Метод линеаризации, эквивалентный медленно меняющейся амплитуде, используется при интегрировании нелинейного дифференциального уравнения движения JP A3x p x, x .Где f x, i — нелинейная функция xDa p-малый параметр. Оба метода эквивалентны друг другу и позволяют получить первое приближение в виде x esini .Где a a t — медленно меняющаяся функция времени. Найдем фазу колебания в виде A , используя метод медленного изменения амплитуды ван-дер-поля. Где k-константа. Для метода эквивалентной линеаризации Крылова и Боголюбова форма 4 0 Чa, a , где A-константа. Решением уравнения X — — k x p-f x, Ji будет являться интегрирование системы из 2 приближенных дифференциальных уравнений.
Как медленно менять амплитуду Второй Д Ф sin , Ак cosф cosф ф — 2haaAsoeff ФХ Ф б эквивалентный метод линеаризации АО соб Собф COS f s f Куда Ф со т. грех Ф ashsoef ПФГ Ф Степень сложности и объем вычислений при решении этих задач практически одинаковы. С помощью метода малых параметров, описанного выше, не только 1-е и 2-е приближения, но и p. даже член, содержащий 8, может найти решение, но объем вычислений резко возрастает без существенного изменения результата. Координаты Дж обратите внимание, что метод малых параметров используется для нелинейностей, которые зависят только от fe4x ц f x , и 2 метода данных могут использоваться для нелинейностей, которые зависят от координат и обоих.
Время воды. k2x П. — Ф Х, р. Например, если вы хотите интегрировать дифференциальное уравнение движения x k2x — p 1 Px L, вы можете использовать метод медленно меняющихся амплитуд или эквивалентную линеаризацию, но с меньшей амплитудой. Параметры. Задание 20.12.Нагрузка массой m показанная на рисунке A в виде в плане перемещается по линейной guide. In центральное положение, он Он находится в контакте с 2 пружинами, которые не искажены и не прикреплены. Коэффициент упругости каждого из них равен СХ. Вибрация нагрузки на границе KL 2l возникает попеременно под действием 1 из этих пружин. Если вибрация превышает KL 2Z, то нагрузка контактирует сторону Пружина предварительного натяга.
Общий модуль упругости основной пружины и 2 боковых пружин составляет около 2.Сила упругости всех пружин отличается в соответствии с законом крюка. На рисунке б показаны свойства упругого элемента force. It состоит из прямых При заданных начальных условиях движение груза x I соответствует уравнению Ш-х-и-синаиф. В это время нагрузка соприкасается с боковыми пружинами. арксинуса-л.
- Форма уравнения движения х Zcos Ай ПК грех. С момента привязки m обратный отсчет начнется снова с нуля для того, чтобы вписаться в эти 2 уравнения движения, уравнение координат f Tv и проекция скорости будут выполнены Gru8 достигает своего крайнего положения через t секунд с этого момента Стыковка внутри Амплитуда колебаний Т5-Г G Ч — В Период колебаний равен r 4, 1 Tj 4 Cdna. я. МТГ 3 я. В заключение, для решения этой задачи следует отметить, что нелинейность системы не мала, поэтому нельзя использовать метод малых параметров, медленно изменяющихся амплитуд и эквивалентной линеаризации. Задача 20.13.An упругая невесомая балка, зажатая на конце О рисунок а, соприкасается с изогнутой guide.
При этом те части балки, которые не соприкасаются с направляющими, становятся короче и тверже. Груз а массой Т крепится к концу балки. Проекция на горизонтальную ось x силы упругости, приложенной к нагрузке, равна Gr — cx-usx рисунок B и равна 0 y 1. Найти уравнение движения груза x f t .Если в первый момент x a высвобождается без начальной скорости, только отклоняясь от вертикального равновесия. Решение. Запишите дифференциальное уравнение mX Fx для движения в виде Fx — cx-axx Г идеальной отправной точкой для экскурсий —ый rh3, 1 Здесь, кг-с т, п г г г к.
Для этого надо знать коэффициент упругости проволоки с и измерить период колебаний Т подвешенного твердого тела. Людмила Фирмаль
Если существует малая нелинейность p-малый параметр, то уравнение 1 может быть решено одним из трех способов малым параметром, медленно меняющейся амплитудой и эквивалентной линеаризацией. Решите задачу с помощью метода малых параметров и найдите циклическое решение Уравнение 1 до члена разложения, содержащего малый параметр в степени 1 Где Xi, Xi-периодическая функция ранее неизвестной циклической частоты p и множества циклических частот в ней Р А ут1. Где ah-константа, которая будет определена позже.
Дифференциальное уравнение 1 сводится к системе уравнений Jfo p x0 0, A P 1 1 oI Найдите правильное решение х0 со пт Х1 потому что 3 ПТ-потому что ПТ Вт Здесь J j a .Уравнение 3 определяет первое приближение решения уравнения 1.
Член, содержащий 1-й порядок p, то есть искомый закон движения вплоть до 2-го приближения Х Х9 XXJ а потому что ПТ п потому что 3 ПТ-ЦОС ВЧ, 4 Где p yA , а циклическая частота p равна П КЛ П-Г 5 Если мы перейдем от 2-го приближения к 3-му приближению, то найдем решение x и круговую частоту p в следующем виде Х х0 pX1 Р2 б Р2 А8 АТС п cta Где xi-неизвестная периодическая функция, a-неизвестная постоянная, и уравнение добавляется в систему уравнений 2 Л — 1 вол — я а — о-3xjxj.
Найдите правильное решение х T024F потому что 5пт coipf Т Где Oj искомое 3-е приближение, включающее малый параметр p, имеет следующий вид х а со пт п — потому что 3пф-cosp0 Игрушка Cos 5pt cospV 6, где меньший параметр p yAa, а циклическая частота равна Р А х й Фе — Ф1-ум ФТИ — 7 если b 1 см, 1 yA 0,1 La, то циклическая частота вследствие нелинейности системы возрастет на 3,75 В до члена, содержащего p первого порядка см. уравнение 5.Сумма вычислений увеличивается в 2 раза r. переход от 2-го приближения к 3-му приближению до a см. уравнение 7 изменяет предыдущий результат на 0,01 L.
Поэтому целесообразно ограничиться поиском решений формул 4 и 5, содержащих 2-е приближение, то есть первый из малых параметров P. При решении этой задачи способом, который изменяет амплитуду медленно, ищите вакцину движения в виде x a 0 W a 0. 8 Интегрирование дифференциальных уравнений 1 сводится к решению системы уравнений. ,. . а 18Т Итак, a f Clt a p — —y Cs, то есть A С Sin A l C2j. начальные условия перемещения движения t Q, x a, 0 дают a, C, 2.То есть решение 7, которое в конечном итоге получается, принимает вид Х со пт 9 Где это показано Чтобы решить эту проблему в движении баккон Эквивалентный метод линеаризации, который мы ищем а 0nnf.
Интегрирование дифференциального уравнения 1 приводит к решению системы уравнений Д 0, фи 1 П4 —. Так… Подставляя a r и ip Z в Формулу 11, мы вычисляем константы Ct и Ca, а затем получаем результат 9 и 10, который находим в методе медленного изменения амплитуды. Если сравнить формулы 10 и 5, то 9 и 3, то мы увидим, что значения циклических частот, определяемые 3 различными способами и закон движения груза одинаковы.
Смотрите также:
Предмет теоретическая механика

