Оглавление:


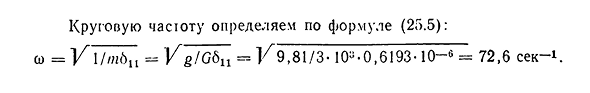

Свободные колебания системы с одной степенью свободы
- Свободная вибрация системы с определенной степенью свободы Когда упругая система отклоняется от равновесия под действием внешних воздействий (удар, отклонение) и устраняет это влияние, система колеблется вблизи положения статического равновесия. Вибрация
такой системы называется свободой. Свободное колебание продолжается до тех пор, пока заявленная начальная энергия не будет израсходована достаточно для работы против внутренней силы трения материала и сопротивления среды. Однако сила сопротивления незначительно влияет на численное
значение частоты свободных колебаний, поэтому при определении частоты Людмила Фирмаль
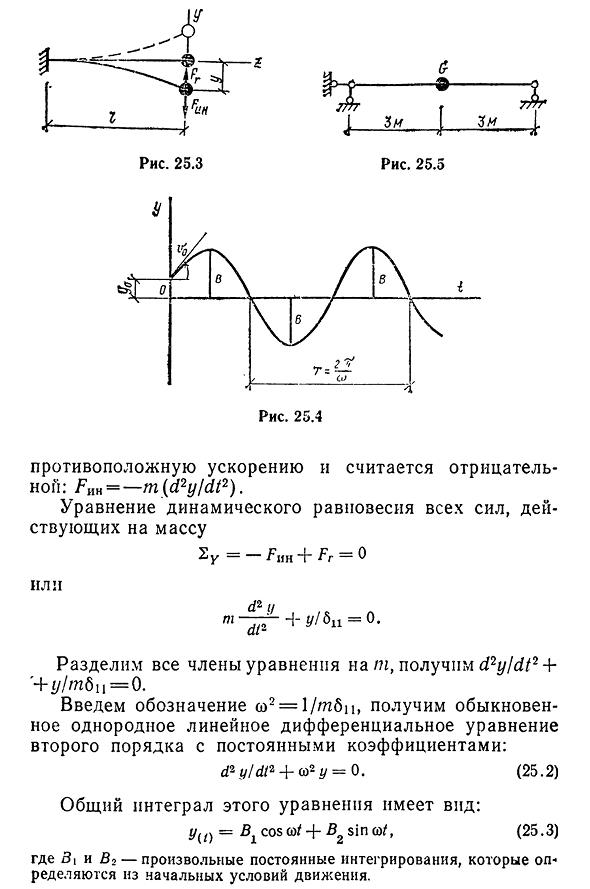
свободных колебаний они не учитываются, то есть частота свободных колебаний. Свободная вибрация системы с некоторой степенью свободы рассматривается в случае консольной балки с массой t без веса. 25.3). Предполагается, что поперечная вибрация массы Т возникает на плоскости вытяжки за счет изгиба упругой балки, хотя и в невесомости. Принцип Далама-Бера применим к уравнению
движения свободных колебаний массы M. из положения равновесия массы y (рис. 25.3). 1) восстанавливающая сила Fr-сила упругой реакции системы, возникающая при отклонении массы t \ восстанавливающая сила Fr пытается вернуть массу в положение статического равновесия, восстанавливающая сила в направлении, противоположном смещению, пропорциональна величине
- отклонения y и жесткости балки Hz: Fr-g n Y-y/^iif где смещение от силы, равной силе, приложенной к точке b’assa t в направлении смещения; 2) сила инерции равна произведению массы на ускорение, то есть на вторую производную пути или перемещения во времени. Эта сила, 283). 25.3 Противоположное ускорение считается отрицательным: Fnn= — m (d2yldt2). Уравнение динамического равновесия всех сил, действующих на массу 2Y= — F » H+Fr=0 Или Д2. +^
/ 611=°- Разделить все члены выражения NAT, получпмы2u/b//2 4- g+g/ / TBC=0. Введем обозначение (O2=1 / TBC, получим нормальное однородное линейное дифференциальное уравнение квадратичного типа с постоянным коэффициентом: d2r/ / d / 2+0) ((25.4), где B=//UD+(g>o/<«) 2-представляет собой максимальное отклонение массы(амплитуды) от положения равновесия.cp0=arctg cog / o / ^o-называется начальная фаза колебания или фазовый сдвиг времени. Постройте график вибрации в соответствии с этим уравнением(рис. 25.4). Повторение значения отклонения y (t) происходит через 2 л/сек, потому что если подставить формулу (25.4)
вместо значения t/*=/+2l/co==/+T, то получится такое же отклонение.: Людмила Фирмаль
y{t}=sin(co/+F0)=sin[co (t+2l/co)+cpj. Таким образом, величина T=2l/co представляет собой весь период колебаний, то есть период до тех пор, пока колеблющаяся масса не вернется в исходное положение. Так,= — это частота свободных колебаний в 2 л секунды, называемая циклической частотой или периодической частотой. В исходное дифференциальное уравнение было введено значение CO2=1 / TBC. Из этого соотношения получаем простую формулу, определяющую частоту свободных колебаний для системы определенной степени свободы: co=V1/ / PBP. (25.5) Частота свободных колебаний является
динамической характеристикой конструкции. Он увеличивается с увеличением жесткости системы 1 / BC, а также увеличивается с увеличением массы т. и уменьшается. Например. Определить круговую частоту свободных колебаний сосредоточенной нагрузки 0=3кн, расположенной в середине однопролетной стальной балки(рис. 25.5). Собственный вес балки (двутавровая балка № 24) не учитывать. Модуль упругости е=2,1. 105 МПа, L=3460cm4. Решение. Отклонение луча 6N в направлении перемещения массы определяется по формуле 6C=/3 / 48E / x, bi=63/4 8-2, 1-105•10E-3460-10—8 = 0,6193.10—®. 285круговую формулу определяли по частоте(25.5): s=У l/m bn=у g/G6n=у 9,81 / 3-10-0, 6193-10-в=72,6 секунды-ч
Смотрите также:
Решение задач по технической механике
| Расчет троса при подъеме груза | Вынужденные колебания системы с одной степенью свободы. Резонанс |
| Понятие о колебаниях сооружений | Приближенный способ расчета на удар |

