Оглавление:















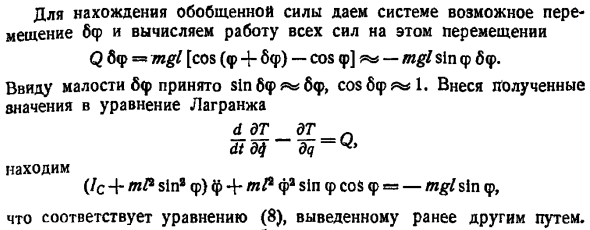

Свободные колебания системы с одной степенью свободы
- Система 6es свободно отбрасывает с усилием сопротивления. Механическая система называется системой 1 степени свободы, если ее положение в пространстве уникально. Она определяется присвоением одной величины q, называемой общими координатами. Движение системы в пространстве описывается временной зависимостью обобщенных координат. Возьми это. Рассмотрим положение начала координат обобщенной системы и устойчивое равновесие нулевого уровня потенциальной энергии, малое движение системы вокруг этого положения равновесия. Отклонение системы от положения равновесия при выборе такой опорной точки определяется величиной обобщенных координат.
Предположим, что составлено небольшое дифференциальное уравнение В случае движения по общим координатам и малой величины общей скорости, которая отсчитывается от положения равновесия, она ограничивается линейным членом дифференциального уравнения движения. Этот. Метод отбрасывания в терминах нелинейных дифференциальных уравнений, включающий квадратные и более продвинутые обобщенные координаты и скорости Линеаризация уравнения. Конечно, такая линеаризация в некоторой степени искажает действительный образ движения, но тем меньше отклонение системы от устойчивого положения Если она находится в равновесии, то линеаризованное уравнение движения системы описывается более точно.
Кольцо совершает сложное движение, которое можно разложить па относительное по отношению к проволоке и переносное вращательное вместе с проволокой вокруг вертикальной оси х. Людмила Фирмаль
Линеаризация дифференциальных уравнений позволяет получить замкнутые решения таких систем. Как правило, невозможно найти точный Интеграл системы нелинейных уравнений в ее окончательном виде. Удобный способ создания дифференциального уравнения малой вибрации В системе используется уравнение Лагранжа. Эти уравнения системы с 1 степенью свободы, где t-кинетическая энергия системы, обобщаются координаты q и обобщенная скорость q-обобщенная сила.
Кинетическая энергия системы, на которую воздействуют стационарные связи, выражается формулой t-j в терминах обобщенных координат и скоростей. Л 2, где q-положительная функция обобщенных координат q. Затем, чтобы линеаризовать выражение кинетической энергии, ряд Маклорина Л-Л0ЛО7ЦИв,.
Разверните вопрос .Это значение уравнения 2 равно Г1Л0 4л0 4 .4 .Затем, предполагая, что dn мал, для краткости он приближается к S, где константа A 0 обозначается a .эта константа всегда Положительный .Это называется коэффициентом инерции .Для линейных обобщенных координат коэффициент инерции a имеет размерность массы, а для угловых координат-размерность момента Инерции твердого тела .Потенциальная энергия системы является функцией обобщенной координаты ПП9 .6 разверните эту функцию в макросерии вблизи положения устойчивого равновесия п-п .0 p-0, 1p-0, h-и h .. 7 в этом уравнении p 0 0, 8.
Это происходит потому, что положение равновесия выбирается относительно нулевого уровня потенциальной энергии. Обобщенная сила положения равновесия Итак, поскольку он равен нулю, строка 7 начинается с пункта 3. Отбрасывание членов более высокого порядка и указание краткости p 0 дает p us, 10. Где константа находится c называется квазиупругим модулем упругости. В случае устойчивого равновесия с 0.
Введение кинетической энергии 5 и потенциала 10 в уравнение Лагранжа 1 Дифференциальное уравнение для малых свободных колебаний системы со степенью свободы от 0 до 1. 11. Это уравнение имеет структуру, аналогичную свободному дифференциальному уравнению. Изменение массы, возникающее под действием линейной восстанавливающей силы. Общая форма интеграла в уравнении 11 дана для простоты. Где l-амплитуда Колебаний, a-начальная фаза, т а-фаза колебаний, а-круговая частота вибрации, часто называют просто частотой вибрации. Определены амплитуда и начальная фаза колебаний В соответствии с начальными условиями.
Если обобщенные координаты в t q и начальные значения их производных равны 0, о, то период колебаний-t-2 k-14 свободен, или иначе получается соответствующее значение. Вибрация системы, определяемая уравнением 12, является гармонической вибрацией. Их частота и период не зависят от исходных данных-эта характеристика называется малой изохронностью Колебания. Заметим, конечно, что дифференциальное уравнение свободной вибрации 11 может быть описано без применения уравнения Лагранжа. Когда решить проблему бесплатно 1 вибрация системы dof, следующие шаги порекомендованы.
Первый способ-применение уравнения Лагранжа 1 и выбор обобщенных координат q 2 В системе выражений кинетической энергии g3 можно найти только потенциальную энергию p или вычислить значение обобщенной 4 путем подстановки g и p. Выражение обобщенной силы в уравнении Лагранжа, получение дифференциального уравнения малой вибрации b путем интегрирования этого уравнения и определения любой интегральной постоянной. Найти уравнение движения системы 6 и определить период колебаний и другие искомые величины.
Второй способ заключается в применении одного из основных уравнений динамики или 1 общей теоремы динамики Система 1 основана на условиях задачи, дифференциальных уравнениях-основных уравнениях динамики, теореме движения центра инерции, теореме изменения- Применяя выбранную теорему, теорему об изменении основного момента кинетической энергии, импульса 2, Составляем дифференциальное уравнение малых колебаний системы. 3 интегрируем это дифференциальное уравнение и определяем любую интегральную постоянную из исходных данных 4 находим далее искомую величину периода колебаний и покоя. Вопрос 18. 6.
Устройство, предназначенное для определения коэффициента трения скольжения между сухими поверхностями, рис. а, прямоугольный металлический блок размещен горизонтально 2. Плоскость de на двух цилиндрах вращается в противоположных направлениях вокруг неподвижных осей a и b. Центр тяжести блока равен g, , , x a x задача 18. 6. Высота h от плоскости ДЕ. Расстояние ab 2a. At в первый момент центр тяжести сместился от центрального position. As в результате блок начал совершать гармонические колебания периодического g. Трение скольжения между блоком и обоими цилиндрами одинаково, найти коэффициент трения скольжения. Решение.
Мысленно отбросьте цилиндр и замените действие обычной реакцией rj. R2 и сила трения frlt frt рисунок b. Сила тяжести блока r приложена к центру тяжести. Создайте дифференциальное уравнение для плоского движения блока, учитывая, что блок не движется. Вдоль оси y и МЯс инерции вокруг центра, чтобы не вращаться — — -р, — Шmj c ri rj-p 0, 2 mra-х-riвхrift-frjh 0. 3 ри-л х ра РЖ хр откуда введите это значение в уравнение 1 и вы найдете дифференциальное уравнение движения r -, r 7s-tax.
Это дифференциальное уравнение для свободных гармонических колебаний. Периодичность этих колебаний равна 4пДgp 4n задача 18. 7, где искомый коэффициент трения скольжения определяется следующим уравнением рама балансировочной машины От рычага ab, который может вращаться вокруг неподвижной точки c, его центр тяжести, стержень bd и диск e будут соответствовать установленному валу od. Конец o. Концы рычагов a и b соединены вертикальной пружиной с неподвижным основанием. Вес Рычага АВ равен 12 г.
Радиус инерции к проходящей горизонтальной оси 3. Проходя через центр тяжести С, который равен dm. Вес q сечение вала od 2 кг является постоянным. Вес диска e составляет n 4, 5 кг. Коэффициент жесткости каждой пружины составляет cj 32 кг ДМ. Размеры ac 2 dm, ac 12 dm, oe m dm, de 4 dm определяют частоту собственных колебаний системы, игнорируя вес тяги bd. Масса диска считается сосредоточенной в точке Е. Для Чтобы найти собственную частоту системы, мы применяем уравнение Лагранжа. Система имеет 1 степень свободы. Выберите угол поворота рычага ab в качестве обобщенной координаты. Указывает этот угол q. Кинетическая энергия системы равна t-l. 1 выпуск, 18. 7.
Где 1lv-момент инерции Рычага АВ к горизонтальной оси через центроид С. od-неподвижный вал момент инерции вала od и угол поворота вала phx-od, вместе с диском установленным относительно горизонтальной оси до конца o. in небольшое движение Вертикальные перемещения точек b и d являются equal. So bc-tf является od-tf, дифференцируя 2 во времени и подставляя значение px в 1, кинетическая энергия равна Перейти к обобщенной скорости 3 обобщенный расчет силы. Горизонтальное положение рычага — это положение статического равновесия. Показывает угол поворота рычага ab Это соответствует переходу из ненапряженного состояния пружины в равновесное положение.
Бесконечно малое приращение bf от положения равновесия, направленное на угол По часовой стрелке, все показатели работы основания силы для 6a-cx ac 2 f f fst bf-cc rc f bf—n-oe-q-t h 6a-ci ac 1 f bf-cx df bf—g, pm 1, bc q. N-oe s q 6f 4, 2, согласно k sun od. Здесь основная работа упругих сил типа пружины а рассчитывается по формуле b ax-f bx-sa x xst bx-ciac f ac bf-ch acr f fet bf. By добродетель В уравнении равновесия угловые скобки 4 равны нулю, поэтому это 6a bf-ckf ac 1 bc 1 bf, а обобщенная сила q, — c1v ac 1 sc 2. To составьте уравнение b-Лагранжа Подставим значения кинетической энергии 3 и обобщенной силы из b. Получим ld iod j-Ф-cxac 1 bcpjФ.
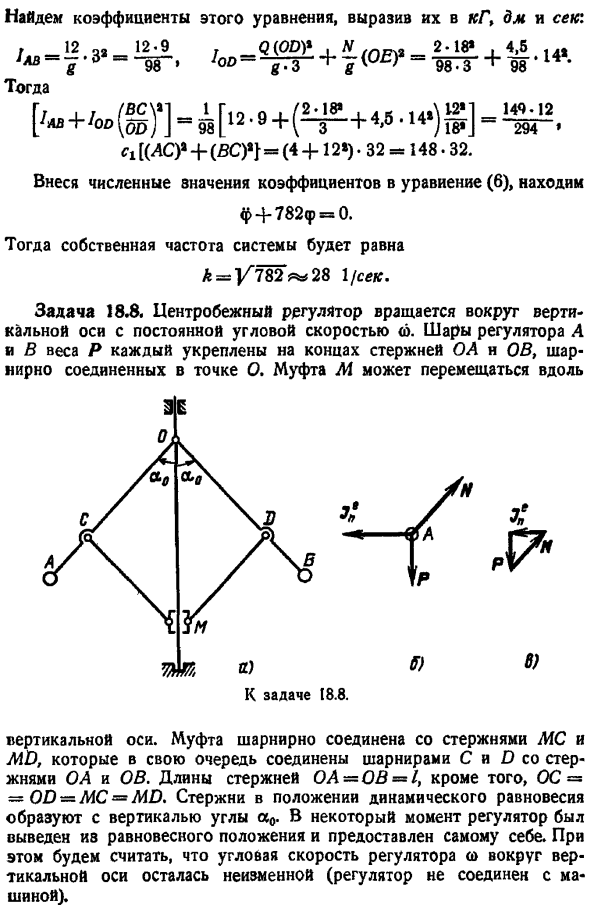
- Найдите коэффициенты этого уравнения и выразите их в следующем порядке kg, dm, sec, c1 -КАК ac 4 12-32 148. 32. Вводя численное значение коэффициента в уравнение 6, находим f 782 p 0. Собственная частота системы v782 равна 28 1 секунде. Задача 18. 8. Центробежный регулятор вращается вокруг вертикальной оси с постоянной угловой скоростью. Регуляторы a и b веса p поворачиваются к концу стержня od n ob соответственно. Он соединен с точкой o. Муфта m может перемещаться вдоль вертикальной оси.
Муфта шарнирно соединена со стержнем mc и md и соединена со стержнем шарниром c и o. ПРО А и ОВ. Длина стержня oa-ov 1, далее os-0d mc md. Стержень в положении динамического равновесия образует вертикальную линию и угол a0. At в один момент регулятор отключился. Вышел из равновесия, предоставленный самому себе devices. In в этом случае угловая скорость регулятора w вокруг вертикальной оси не изменяется, и контроллер Найти период малых колебаний вблизи положения равновесия. Масса стержня и муфты игнорируется.
При относительном криволинейном движении материальной точки удобно пользоваться дифференциальными уравнениями движения в проекциях на оси натурального триэдра. Людмила Фирмаль
Мяч a и b рассматриваются как важные точки. Решение. Разделите раствор на 2 этапа. Во-первых, положение динамического равновесия системы определяется кинетическим методом statics. In Фаза 2, используя уравнение Лагранжа с обобщенными координатами Найти дифференциальное уравнение для малых колебаний системы и частоты и периода этих колебаний. Первая ступень. Примените метод статики движения к шару а в положении динамического равновесия. Шар фигура ТФ актов по тяжести Р, Шатун Н реакция направлена вдоль стержня АО. Согласно методу кинетической статики, эти силы должны компенсироваться силой инерции j.
При вращении с постоянной угловой скоростью c вокруг вертикальной оси существует только сила вертикальной инерции, равная по абсолютной величине j ml sin aoco, которая является массой шара. 3 Мощность jk p, n можно рассматривать как фигуру. tf. Создайте схему треугольника мощности. c, оттуда найти p tg 0 jn mzsinoofind. Отсюда, угол о Положение w 2-я стадия динамического равновесия. Дайте угол od, образованный стержнем с небольшим вертикальным шагом ba.
Шарик начинает мелко вибрировать Рядом с положением равновесия. Регулятор представляет собой систему с 2 степенями свободы. Возьмем обобщенный координатный угол a. Это позволит определить отклонение шарика и стержня Это угол от вертикали, где угол Р — угол поворота регулятора вокруг вертикальной оси. Создадим первое уравнение Лагранжа обобщенных координат a. Рассмотрим движение шара как составное Найти абсолютную скорость шара по переносному вращению вокруг вертикальной оси и теорему сложения относительной скорости вращения вокруг горизонтальной оси через точку o Переносные и относительные модули скорости такие же, как iv zsina o zsina-q, vr 1a.
Обратите внимание, что vr находится на плоскости, которая совпадает с ромб oabm, и v перпендикулярно этой плоскости. Г 2 В, П Ф2 грех 4-й. Кинетическая энергия 2 шаров равна 3. Перейдем к определению обобщенных сил. Вертикальные координаты шара z равны 2 zcosa. Его вариация-6z-zsinada. Основная задача гравитации, которая является единственной активной силой, приложенной к системе, 2r — это 6 a 2p dz-2p1 sin a ba. So обобщенная сила-это qa- 2pzsina. 4.
Если подставить найденную кинетическую энергию и обобщенные значения силы в уравнение Лагранжа, то получим dt да 2 f sin a cos a. 5 замена dt, согласно 2-му, b 2 вместо 7 2 atcsl w s f — — — — — — — — 2w ln и 6, или производная коэффициента, деленная на, а, noting-ш2sin aepcos a, Р-sin ao r найдена. 7 угол р, согласно условиям — Небольшое количество. В результате, грех А0 П и грех С С ко п п потому что, потому что ОО п потому что АО-psinctg, где примерно греха П и п, потому что п i1. By введя значение 8 и заменяя г л в cosпо 1 В уравнение 7, получаем 0-грех чч 0 А0 А0 А0 потому что потому что-0 грех куб. См 4-и cos СС Син о 0 потому что А0 0 или 0 СО2 грех аб0 грешить, потому что А0 00 0.
Потому что ao02 второй размер Для меньших порядков мы в конечном итоге находим дифференциальное уравнение свободных малых колебаний центробежного регулятора e, sin al 0 0. 9 частота свободных колебаний равна sin a, , В a. Период свободных малых колебаний был равен угловой скорости 10, и 2-е уравнение Лагранжа, соответствующее обобщенной координате р, не требовалось. Это и есть условие Задача изменяет набор координат.
Его производная-регулятор постоянен при вращении вокруг вертикальной оси. Задача 18. 9. Груз веса Р подвешен нерасширении нить АБ. Он набрасывается сверху на блок с неподвижной осью o. Вес блока f. Его масса равномерно распределяется по поверхности круга с радиусом d. Конец резьбы b прикрепляется к вертикальной пружине, а коэффициент с одинаковой жесткостью. Определите изменение нагрузки.
Если в первый момент груз неподвижен, то его вес уравновешивается натяжением пружины, и сообщается начальная скорость v0 Трение между осью нисходящего блока и подшипником игнорируется. Вес нити игнорируется. Решение. Используйте 2-й вид уравнения Лагранжа. Выберите ось x начинается в положении равновесия груза и направляет его вертикально вниз. Тогда координата x нагрузки в любой момент времени полностью определяет положение системы. Это считается корректировкой сообщества.
Кинетическая энергия системы-это сумма кинетической энергии нагрузки и кинетической энергии агрегата. Скорость Груза Поскольку скорость и величина точек на ободе блока равны, окончательное представление кинетической энергии системы обобщенной скоростью принимает вид Дает системе возможное движение bx и составляет основную задачу данной мощности. Основная работа заключается в работе силы тяжести груза и силы упругости пружин 6Д П ЛК-ы х д р ВХ-х Д-в ы х ВХ-СБХ. В состоянии равновесия это СД Р.
Буква d указывает на статическое удлинение пружины. Обобщенная сила-это коэффициент, когда это возможно. Перемещение bx в начальной школе работа q формула. 1 заметим, что в этой задаче обобщенная сила q может быть легко вычислена другим способом. Давайте создадим выражение возможности Энергия системы выбора нулевого положения равновесия груз П. В свою очередь, Н-lr и обобщенной Си. 11 матчей 1. Создайте уравнение Лагранжа. Или потому что bt dx это решение Однородные линейные дифференциальные уравнения с постоянными коэффициентами имеют вид x a sin ktp, 2. Где частота a находится из уравнения p 0.
Любая постоянная Интегралы a и 0 определяются из начальных условий t 0, и существуют x0 0, jjg-og. Если вы присвоите эти значения 2, вы найдете oa sinp или р0. Затем из 2, чтобы получить Ак, потому что КТ введение значения любой константы при i0 t 0 ak или 2 в конечном итоге даст x в sin at. Цикл свободных колебаний нагрузки равен задаче 18. 10. Масса q и радиус Горсуча g удерживается в равновесии на идеально гладкой горизонтальной поверхности резьбой ab. In в этом случае плоская часть поверхности полусферы образует горизонт и угол. a. Определите после Обрыв резьбы ab, скорость центра o и ее максимальное, наибольшее давление полушария на горизонтальную плоскость.
Кроме того, предполагая, что угол a мал, длина становится короче Эквивалентный математический маятник. Решение. После того, как резьба нарезается, Рис. 2 силы действуют на всем полушарии. Это реакция веса q и гладкой плоскости Н. Обе силы направлены вертикально. Согласно теореме о движении центра инерции, ускорение центроида С также направлено вертикально. Начальная скорость точки С, а также других точек полушария Если она равна нулю, то центр инерции перемещается в вертикальном направлении по прямой линии. Центр полусферы o находится на некотором расстоянии r от гладкой плоскости. Перемещение по горизонтальной линии параллельно плоскости отсчета.
Таким образом, скорость точки с направлена вертикально, а скорость точки о направлена горизонтально. Восстановление до скорости 2 из этих 2 точек являются вертикальными, поэтому мы находим мгновенный центр скорости a b. Примените теорему изменения кинетической энергии для перемещения полушарий с самого начала Положение, определяемое углом a, при любом положении угла p получает 44 cos f-cos a представляет ОС. 1 слева от уравнения находится уравнение кинетической энергии В конце движения, в первый момент, кинетическая энергия ручара была равна нулю, потому что ручар был неподвижен.
На правой стороне рассчитана работа силы тяжести при переходе полушарий От начального положения до конечного положения. Эта реакция направлена перпендикулярно движению точки d, поэтому работа реакции n равна нулю. Момент инерции полусферы относительно момента Для ic tp sin8 p центр скорости может быть выражен на основе теоремы Штейнера следующим образом 2 Итак, если известна функция угла. Айкью-определить момент Инерция пола шара направлена к горизонтальной оси, которая проходит через центр инерции и перпендикулярна плоскости чертежа. Равномерный момент инерции шарика 2 0 Центральная ось равна 2 0-mg 2t g. Здесь m 2t-масса однородного шара.
Затем формируется равномерный момент инерции полусферы относительно горизонтальной оси, которая перпендикулярна плоскости чертежа Проходя через точку О, расстояние центра инерции полусферы от точки о равно zr 8. Используйте теорему Штайнера, чтобы создать это значение с помощью −1, -tp-a mr-iт И-Л. В уравнении 2 r mr tp sin r tr c sin f. Для краткости, если вы укажете 83 45 секунд, вы получите cozy-cos от 1 до 2g и s sin y 3 4 5. Скорость точки o центра половины шара равна тому же значению, что и v0 op. ВМ со ф потому что j в точке o скорость f 0.
Смотрите также:
Предмет теоретическая механика

