Оглавление:


Свободное кручение тонкостенных стержней
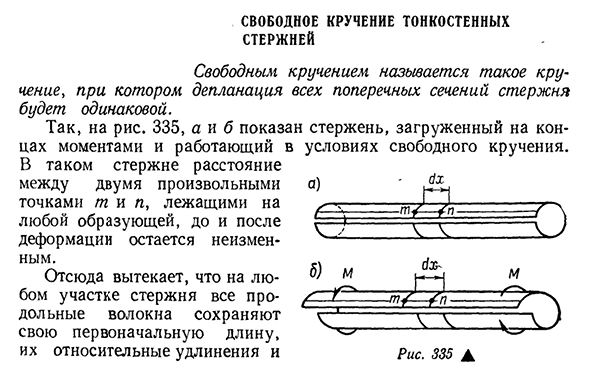
- Кручение тонкой стены свободное Стержень. Свободный поворот-это поворот, при котором отклонение всех поперечных сечений стержня становится одинаковым. Итак, рисунок показывает. 335, a и b показывают времена и штанги нагруженные к концу с возбуждениями под свободными условиями кручения. В таком
стержне расстояние между двумя произвольными точками t и n на любой шине до и после деформации не изменяется. В любой части стержня все продольные волокна сохранят свою п
ервоначальную длину, удлинение и удлинение. Но) а’х ——‘ б) м / сек- ■ м Рис 335D ■ Людмила Фирмаль
392 укорочение будет равно нулю (El=0). Таким образом, поперечное сечение стержня имеет только тангенциальное напряжение, а нормального напряжения нет. В Главе VII 61, когда полоса с прямоугольным поперечным сечением скручена, поток
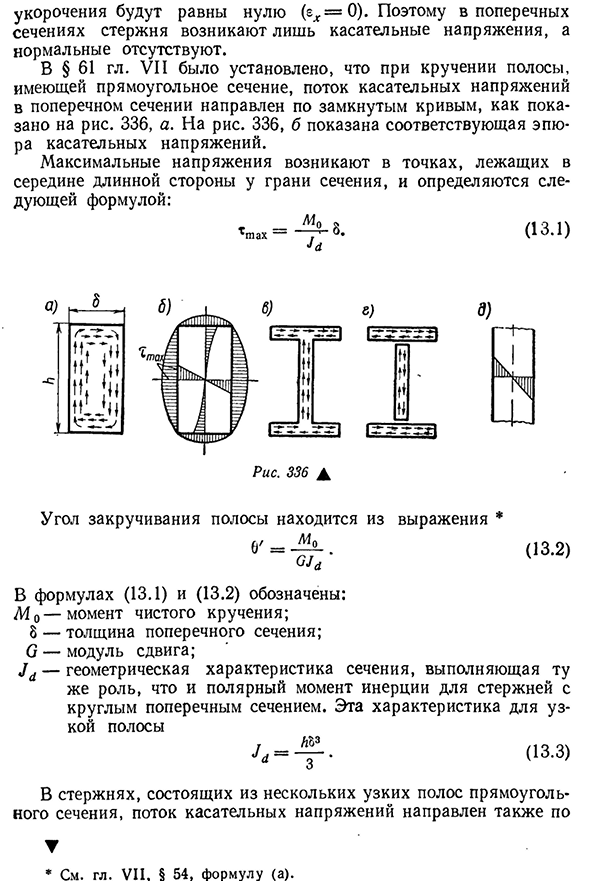
тангенциального напряжения в поперечном сечении направлен вдоль замкнутой кривой, как показано на рисунке 336. Как использовать 336, b показывает соответствующий график касательного напряжения. Максимальное напряжение возникает в точке посередине длинной стороны торца сечения и определяется по
- формуле: Рис 336а Угол скручивания полосы находится из выражения * (13.2) Формулы(13.1) и (13.2) задаются следующим образом: M o-момент чистого кручения; 8-толщина поперечного сечения; O-модуль сдвига;, 1A-геометрические свойства поперечного сечения, эта особенность с закругленным поперечным сечением обусловлена узкой полосой =(13.3) В стержнях, состоящих из нескольких узких полос прямоугольного сечения, поток тангенциального давления
также направлен. История * См. главу VII, главу 54 и выражение (а). 393 замкнутый контур (фиг. 336, в). В таком профиле с достаточной точностью на практике можно предположить, что поток тангенциальных напряжений состоит из ряда замкнутых контуров, как показано на рисунке двутавровой балки 336, а. В этом случае распределение напряжений по толщине поперечного сечения принимается по линейному закону(рис. 336, д’). Таким образом,
на средней линии элемента поперечного сечения тангенциальное напряжение равно нулю. Максимальное значение напряжения Людмила Фирмаль
принимается элементом с наибольшей толщиной в точке, наиболее удаленной от средней линии и расположенной в середине длинной стороны элемента. Формула для определения Ttah имеет тот же вид, что и (13.1), но значение] a в ней, и в этом случае формула (13.2) вычисляется по формуле г=1 Здесь-длина каждой детали, измеренная вдоль центральной линии; — толщина одной и той же детали. Коэффициент а Формулы (13.4) по опыту принимается равным»качению: Р а у Т А д………………………………………………………… 1,20 Вт В Е Л Л Е Р А…………………………….. … …………………….. 1.12 УГ О Л К а………………………………………….. … 1.0 Для сварных двутавровых балок с ребрами жесткости а=1,5. В случае профилей, составленных из рулонных двутавровых балок, швеллеров или углов, определяется величина соединенных сваркой нескольких рядов или одной кромки заклепки. Где<Ha-значение характеристики, рассчитанное для отдельного профиля по формуле (13.4).
Смотрите также:

