Оглавление:




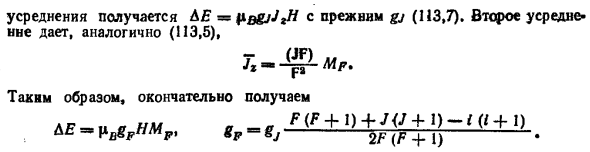

Сверхтонкая структура атомных уровней
- Ультратонкая структура атомного уровня Другой атомный эффект особенно актуален Ядерные свойства расщепляются на атомном уровне Энергия в результате взаимодействия электрона и спинового яда р так называемая сверхтонкая структура уровня. С точки зрения Слабость интервала взаимодействия этой структуры Очень маленький по сравнению с худым Структура.
- Поэтому следует учитывать сверхтонкую структуру Индивидуально для каждого микроструктурированного компонента STI. В этом разделе показано ядерное вращение ( Как это принято в атомной спектроскопии) через г Держите обозначение J каждого момента электронного Атом Атом. Показывает суммарный момент атома (вместе с ядром) Как F = J + я. Каждый компонент имеет сверхтонкую структуру Характеризуется конкретным значением в данный момент Там.
Согласно общему правилу сложения моментов, квантовое число F Принять значение F = J + i, J + i-1. , , , | J-r |, (121,1) Людмила Фирмаль
Каждый уровень с определенным J делится на 2g + 1 (Если r J) компонент. Поскольку среднее расстояние r электронов в атоме велико По сравнению с радиусом ядра R, который является главной ролью ультраконечности Расщепление взаимодействует с электронами и мультиполями Самый низкий ядерный момент. Они Магнитный диполь и электрический квадруполь Момент (см. Zero-§75 для среднего дипольного момента).
Ядерный магнитный момент порядка ^ eDg’yad / s. Где уяд — скорость нуклона в ядре. Его энергия Взаимодействие с магнитным моментом электрона (/ lel ^ eH / ts) §121S V E R X T O N K A I S T R U K T U R A A M O S N Из того, Мед / ^ EL 6 N D ^ id (1 2 1 2) Ядерный квадрупольный момент Q ~ ei? 2; энергия взаимодействия Созданный им эффект поля с электронным зарядом заказа eQ e2 R 2 (, ^ ~. (121,3) Сравнивая (121.2) и (121.3), магнитное взаимодействие.
Действие (и, следовательно, разделение уровня, вызванное этим) c (uyad / c) (H / mcR) -15-кратное квадрупольное взаимодействие Действие; соотношение сояд / с относительно невелико, соотношение ч / м кр большой. Операторы магнитного взаимодействия электронов с ядрами Формат ^ Vu = aiJ (121,4) (Аналогично спин-орбитальному взаимодействию электронов (72,4)).
Зависимость деления уровня от F Так дается по формуле -2 F {F + 1) (121,5) (Ср. (72,5)). Операторы электронного и квадрупольного взаимодействия Составлено квадруполем из тензорного оператора Qik Вектор J компонента ядерного момента и электронного момента. Пропорционально скаляру, состоящему из этих операторов QikJiJk, т-е формат ^ ^ 2 1 ^ ^ «B J {Jk \ (121,6) Qik считает себя представленным оператором вращения ядра Формула формулы (75,2).
Расчет собственных значений оперы Тора (121.6) (это делается точно так же, как вычисление В вопросе 1) § 84 о квадрупольной зависимости Сверхтонкое разделение уровней по квантовому числу F да Представлено F 2 {F + I) 2 + ± F (F + 1) [1-2J (J + 1) -2i (i + 1)]. (121,7) Особенно эффект магнитного сверхтонкого расщепления Это заметно на уровне, связанном с внешней электроникой Прогулка в S-состоянии, учитывая относительно высокую вероятность Факт нахождения такого электрона вблизи ядра.
- Вычисляет сверхтонкое расщепление атомов, содержащее Один внешний 5 электрон (Э. Ферми, 1930). Этот электрон Является ли сферически симметричная волновая функция φ (r) Движение оставшихся электронов и ядер в самопоследовательном поле Поиск операторов электронно-ядерного взаимодействия Как оператор энергии — DN D = fii / i в ядерном магнитном моменте Магнитное поле, созданное электронами (в начале координат).
Согласно известной электродинамической формуле, это поле Где j — оператор плотности тока, созданный перемещением. Спин электрона, r = ng — радиус-вектор от центра Элемент d V2). Согласно (115.4) Сверхтонкий, когда полный атомный импульс J = S = 1/2 После расщепления появляется дублет (F = i zt 1/2).
Согласно (121.5) и (121.9) найдите расстояние между двумя Уровень дублета (См. Примечание на стр. 601). 2) См. II, §43, формула (43.7). Людмила Фирмаль
Обратите внимание, что последний вектор R направлен От льна-дв в противоположном направлении к центру (точка наблюдения за полем). (121,8) j = -2 / iBcrot (V> 2с) = -2fiBc Арканзас (Цвет-Бора Магнетон). Напишите dV = r 2 dr do Запеченный, найти Ах ах 0 Наконец, для операторов взаимодействия: Vis = — £ H = ^ ^ inφ2 (0). (121,9) 61 E i + l / 2-Ei _ 1/2 = U »1lv (2r + l) V-2 (0). (121,10) г) В следующем расчете условие Z e 1 j he 1
Поскольку значение φ (0) пропорционально \ [Z (см. §71), Порядок этого деления увеличивается пропорционально атомам Меры. Z a z h 1. Рассчитать сверхтонкое расщепление Атом, содержащий один элемент за закрытой оболочкой (по действию) Трон с орбитальным импульсом I (Э. Ферми, 1930). Потенциал вектора решения и напряженность магнитного поля, Созданный магнитный момент ядра / I A = 1 H n = Zn [cn] -c g2’g3 (Div A = 0).
Используйте эти выражения для написания операторов взаимодействия В форме — ^ -A p + ^ H s = +3 (sn) n-s]. тс ц г После усреднения с определенным значением j формула ква Двойные скобки расположены вдоль j. Так что вы можете написать _z % = 2 / jb (w) [U + 3 (sn) (n j) -s j] -Г w (ij) U + j (j + 1) Я VI 21 (1 + 1) с J-6 (SL) (JL) ~ Среднее значение cpc было рассчитано для задачи § 29. Если вы переместите их на собственные значения, (21-1) (21 + ч)
После простого расчета, наконец, найти CVC 1 (1 + 1) * j (j +!) F (F + l) r-3 Где F = j + i, a] = I ± 1/2. Среднее значение g-3 в радиальном направлении выполняется Часть электронной волновой функции. 2. Определение зеемановского расщепления сверхтонких компонентов Тур на атомном уровне (С. А. Гоудсмит, Р. Ф. Бачер, 1930). Формула (113.4) (при условии, что поле очень слабое.
Вызванное этим деление мало по сравнению с интервалом (Ультратонкая структура) не средний Не только в электронном виде, но и в сфере ядерного шпионажа Для. Результат первого усреднения, A E = / i B g j J z H г (113,7). Второе среднее такое же, как (113,5) T. = ^ M ,. F Итак, наконец, получить F (F + l) + J (J + l) -i (i + l) A E = jlBgFHMF, gF = g j- 2F (F + 1)
Смотрите также:
| Несферические ядра | Сверхтонкая структура молекулярных уровней |
| Изотопическое смещение | Общая теория рассеяния |
Если вам потребуется заказать решение по физике вы всегда можете написать мне в whatsapp.

