Сведения об экстремуме функции, частных производных, градиенте и производной по направлению
Из курса математики читателю известны простейшие задачи на отыскание точек максимума или минимума функции одной переменной. Функция 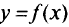 , определенная в точке
, определенная в точке 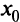 , достигает максимума (минимума) в окрестности точки
, достигает максимума (минимума) в окрестности точки 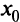 , если для всех точек этой окрестности удовлетворяется неравенство
, если для всех точек этой окрестности удовлетворяется неравенство 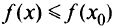 .
.
Максимум и минимум функции объединяют одним названием экстремум. Как правило, точка 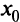 — внутренняя точка естественной области определения функции
— внутренняя точка естественной области определения функции 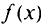 и экстремум называют внутренним. Если существует производная
и экстремум называют внутренним. Если существует производная 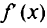 в точке
в точке 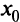 , то функция
, то функция 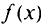 может иметь в точке
может иметь в точке 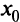 внутренний экстремум лишь в том случае, когда при
внутренний экстремум лишь в том случае, когда при 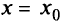 производная
производная 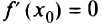 (необходимое условие экстремума). Экстремум может быть и в тех точках
(необходимое условие экстремума). Экстремум может быть и в тех точках 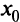 , где производная
, где производная 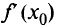 не существует. Но выполнение необходимого условия еще не означает, что в точке
не существует. Но выполнение необходимого условия еще не означает, что в точке 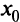 будет экстремум. Для того чтобы в точке
будет экстремум. Для того чтобы в точке 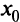 был экстремум, производная
был экстремум, производная 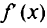 в окрестности точки
в окрестности точки 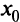 при переходе через
при переходе через 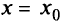 должна менять свой знаке плюса на минус в точке максимума и с минуса на плюс в точке минимума. Можно применить и другой признак: если в точке
должна менять свой знаке плюса на минус в точке максимума и с минуса на плюс в точке минимума. Можно применить и другой признак: если в точке 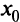 первая производная
первая производная 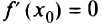 и существует вторая производная
и существует вторая производная 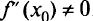 , то в точке
, то в точке 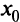 будет максимум при
будет максимум при 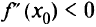 и минимум при
и минимум при 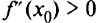
В общем случае, если существуют производные от 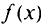 до
до 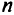 -го порядка включительно и если
-го порядка включительно и если 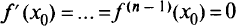 и
и 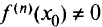 , функция
, функция 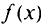 имеет в точке
имеет в точке 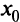 максимум при
максимум при 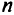 четном и
четном и 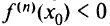 и минимум при
и минимум при 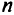 четном и
четном и 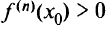 . Если
. Если 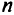 нечетно, то функция
нечетно, то функция 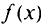 в точке
в точке 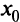 не имеет ни минимума, ни максимумам имеет точку перегиба.
не имеет ни минимума, ни максимумам имеет точку перегиба.
Дадим несколько определений, которые потребуются в дальнейшем.
Действительная функция 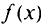 , определенная при
, определенная при 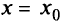 , имеет в точке
, имеет в точке 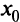 (локальный)максимум или (локальный)минимум
(локальный)максимум или (локальный)минимум 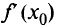 , если существует такое положительное число
, если существует такое положительное число 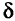 , что при всех приращениях
, что при всех приращениях 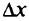 независимого переменного
независимого переменного 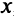 , равных
, равных 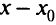 , для которых выполняется неравенство
, для которых выполняется неравенство 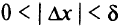 и существует значение
и существует значение 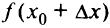 , приращение данной функции соответственно
, приращение данной функции соответственно
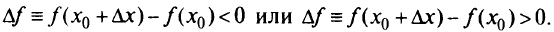
Если в каждом из этих случаев выполняются нестрогие неравенства, то говорят, что функция 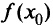 имеет в точке
имеет в точке 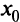 нестрогий максимум (минимум).
нестрогий максимум (минимум).
Локальный (максимум) минимум называют внутренним (максимумом) минимумом или граничным (максимумом)минимумом, если соответственно точка 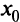 является внутренней или граничной точкой области определения функции
является внутренней или граничной точкой области определения функции 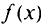 .
.
В формулировке задачи должна быть точно указана область определения функции 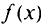 . Например, функция
. Например, функция 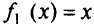 при
при 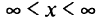 не имеет максимума, а функция
не имеет максимума, а функция 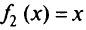 при
при 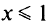 имеет при
имеет при 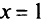 граничный максимум.
граничный максимум.
Если неравенство 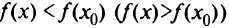 выполняется для любой точки
выполняется для любой точки 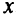 , принадлежащей области определения функции
, принадлежащей области определения функции 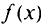 , то говорят о глобальном максимуме (минимуме) функции
, то говорят о глобальном максимуме (минимуме) функции 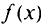 в точке
в точке 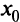 . Аналогичные определения справедливы для функции многих переменных.
. Аналогичные определения справедливы для функции многих переменных.
Функцию 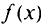 , имеющую в данной точке
, имеющую в данной точке 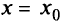 производную, называют дифференцируемой в этой точке; функцию, имеющую производную во всех точках некоторого промежутка
производную, называют дифференцируемой в этой точке; функцию, имеющую производную во всех точках некоторого промежутка 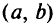 , называют дифференцируемой в этом промежутке.
, называют дифференцируемой в этом промежутке.
Функцию многих переменных, имеющую полный дифференциал в данной точке, области, называют дифференцируемой в этой точке, области. Необходимое условие дифференцируемое™ функции многих переменных — наличие частных производных первого порядка (в точке, в области). Достаточные условия дифферен-цируемости функции многих переменных — существование и непрерывность всех частных производных первого порядка (в точке, в области).
Числовую функцию 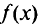 одного векторного аргумента
одного векторного аргумента 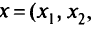
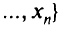 вида
вида
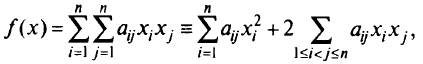
где 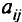 — элементы симметричной матрицы (квадратной таблицы чисел)
— элементы симметричной матрицы (квадратной таблицы чисел) 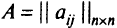 порядка
порядка 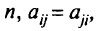 называют квадратичной формой переменных.
называют квадратичной формой переменных.
Квадратичную форму 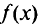 называют положительно (отрицательно) определенной, если для любого ненулевого вектора
называют положительно (отрицательно) определенной, если для любого ненулевого вектора 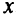 выполняется неравенство
выполняется неравенство
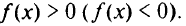
Такие формы объединяют общим названием — знакоопределенные. Если же имеется ненулевой вектор 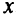 , для которого
, для которого 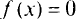 , форму называют квазизнакоопределенной. Квадратичную форму называют знакопеременной, если существуют такие векторы
, форму называют квазизнакоопределенной. Квадратичную форму называют знакопеременной, если существуют такие векторы 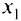 и
и 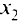 что
что
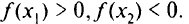
Для наглядного представления поведения функции 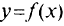 строят график функции. Если независимую переменную
строят график функции. Если независимую переменную 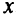 (аргумент) и зависимую переменную у рассматривать как декартовы координаты на плоскости, то действительная функция
(аргумент) и зависимую переменную у рассматривать как декартовы координаты на плоскости, то действительная функция 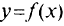 действительного переменного изобразится кривой — графиком функции
действительного переменного изобразится кривой — графиком функции 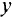 от
от 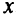 .
.
Для функции многих переменных 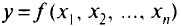 упорядоченному множеству значений независимых переменных
упорядоченному множеству значений независимых переменных 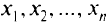 ставят в соответствие значения переменного
ставят в соответствие значения переменного 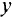 . Множество значений
. Множество значений 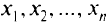 для которых определено соотношение
для которых определено соотношение 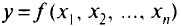 , есть область определения функции
, есть область определения функции
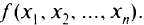
Графиком функции многих переменных является поверхность для функций двух переменных и гиперповерхность — для большего числа переменных. Чтобы представить функцию 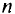 переменных, вводятся понятия линий и поверхностей уровня. Это геометрическое место точек, в которых функция принимает одно и то же значение.
переменных, вводятся понятия линий и поверхностей уровня. Это геометрическое место точек, в которых функция принимает одно и то же значение.
Уравнение поверхности уровня имеет вид
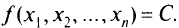
Давая константе 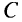 различные значения, получаем семейство поверхностей уровня, определяющих поведение функции. Линии уровня вводятся для функции двух переменных:
различные значения, получаем семейство поверхностей уровня, определяющих поведение функции. Линии уровня вводятся для функции двух переменных:
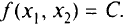
Семейство линий уровня дает возможность представить функцию двух переменных
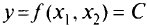
на плоскости. Например, семейство линий уровня на географических картах дает представление и о морских глубинах, и о высоте горных хребтов.
Для характеристики скорости изменения функции многих переменных относительно одной из переменных, например 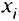 , при фиксированных значениях остальных независимых переменных вводится понятие частных производных
, при фиксированных значениях остальных независимых переменных вводится понятие частных производных 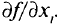 Частная производная
Частная производная 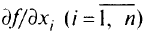 может быть найдена посредством дифференцирования функции
может быть найдена посредством дифференцирования функции 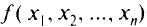 по
по 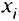 ( если остальные
( если остальные 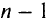 независимых переменных рассматривать как постоянные параметры.
независимых переменных рассматривать как постоянные параметры.
Направление, в котором скорость возрастания функции многих переменных наибольшая, определяется вектором, называемым градиентом. Противоположное направление называют антиградиентом. Градиент скалярной функции
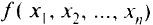
есть векторная функция точки и определяется как
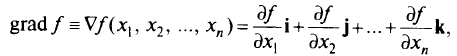
где 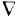 — знак градиента;
— знак градиента; 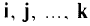 — единичные векторы (орты), направленные по координатным осям:
— единичные векторы (орты), направленные по координатным осям:
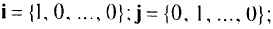
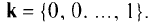
Иногда применяется обозначение градиента в виде 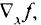 где индекс
где индекс 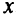 показываем переменные, по которым определяется градиент. Другими словами, градиент скалярной функции — это вектор, координатами которого являются частные производные заданной функции.
показываем переменные, по которым определяется градиент. Другими словами, градиент скалярной функции — это вектор, координатами которого являются частные производные заданной функции.
Скорость изменения скалярной функции
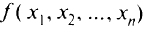
в произвольном направлении, задаваемом единичным вектором
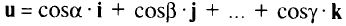
с направляющими косинусами
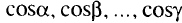
определяется производной по направлению (действительное число)
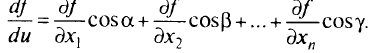
Производная по направлению с градиентом скалярной функции 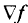 связана скалярным произведением
связана скалярным произведением
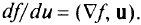
Скалярным произведением двух векторов
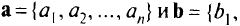
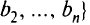
называют действительное число, равное сумме произведений соответствующих координат векторов:
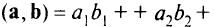
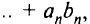
или произведению длин этих векторов на косинус угла между ними,
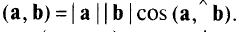
Градиент 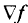 всегда ортогонален поверхности (линии) уровня функции
всегда ортогонален поверхности (линии) уровня функции 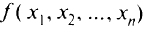 . Действительно
. Действительно

Производная по направлению касательной к поверхности (линии) уровня 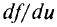 равна нулю,
равна нулю, 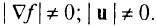 . Поэтому
. Поэтому 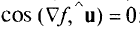 :
:
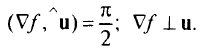
Нам потребуются понятия линейной зависимости и независимости векторов. Векторы 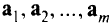 называют линейно зависимыми, если найдутся такие действительные числа
называют линейно зависимыми, если найдутся такие действительные числа 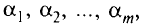 не все равные нулю, что линейная комбинация векторов
не все равные нулю, что линейная комбинация векторов 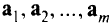 равна нулю:
равна нулю: 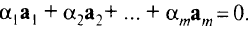 . Если же это равенство выполняется только тогда, когда все числа
. Если же это равенство выполняется только тогда, когда все числа 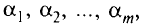 равны нулю, то векторы
равны нулю, то векторы 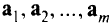 называют линейно независимыми.
называют линейно независимыми.
Из определения линейной зависимости векторов следует, что если векторы линейно зависимы, то один из них может быть представлен в виде линейной комбинации остальных, и, обратно, если один из векторов есть линейная комбинация остальных, то векторы линейно зависимы.
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:

