Оглавление:



Сведение двойного интеграла к повторному
- Уменьшение двойного интеграла для повторных интегралов. Если мы продолжим рассматривать двойной Интеграл как объем
геометрически цилиндрического стержня, мы дадим инструкцию по его вычислению, сведя его к повторяющемуся интегралу здесь:
§ 3371 1. Определение и простейшие свойства 235 В первом томе мы уже Людмила Фирмаль
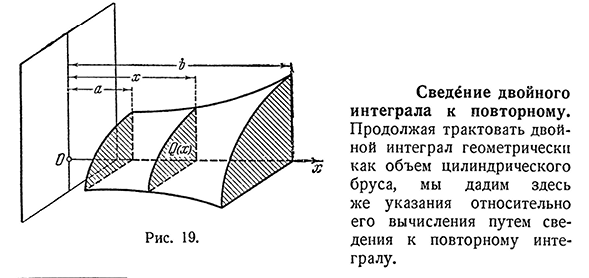
работали над проблемой вычисления объема тела (V) по поперечному сечению[n°198]. Давайте вспомним здесь соответствующую формулу. Обязательно заключите тело в плоскости x=a и x=B(рис. 19).
Предположим, что поперечное сечение объекта с плоскостью, перпендикулярной оси X и соответствующей абсциссе x(a^x^b), имеет площадь<3 (x). В свою очередь, объем тела, предполагающий ег
- существование, определяется по формуле b Y=^(2 (x) s? х (3) Но Теперь применим эту формулу к расчету объема цилиндра предыдущей задачи. Начать На этой фигуре мы получаем ее А-образный дизайн
без искажений Кон. Это было из простого случая, когда основание стержня представляет собой прямоугольник[a, B;C, ( / ] (рис. 20). Поперечное сечение плоскости пучка x=x b (a^X b^B) представляет собой изогнутую трапецию Арзу. Чтобы найти эту область,
мы проектируем плоскость UX\gruent с B & M для (x0)=PL, so. Арзу = ПЛ. Людмила Фирмаль
Зет.^ Но уравнение линии uhzt на плоскости, по-видимому, x=/(x0>>’) (C^y O). Используя известную формулу области кривой как определенный интеграл, мы имеем 3 * o() = ^* (С(х0)] *) Здесь внутренний Интеграл является непрерывной функцией x[см. n°299].
Смотрите также:
Решение задач по математическому анализу
| Связь между криволинейными интегралами обоих типов | Определение двойного интеграла |
| Задача об объеме цилиндрического бруса | Классы интегрируемых функций |

