Оглавление:







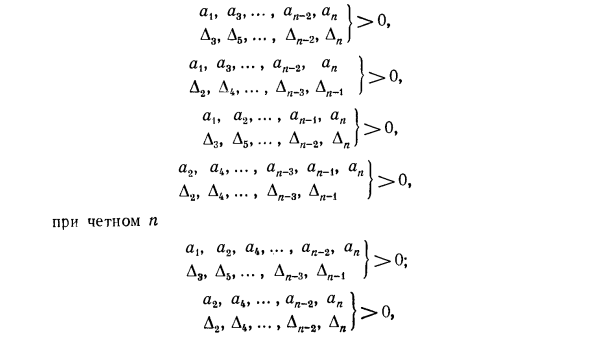




Существующие методы оценки устойчивости с тонки зрения возможностей реализации их на ЦВМ
- Существующие методы оценки устойчивости от тонких аспектов реализации на цифровых компьютерах Опишите динамику самоходной пушки в системе линейных дифференциальных уравнений (6.1) dxjdt = dxjdt = auxt + al2x2 + o2lx (+ a22 * 2 + —- b ainxn + bjt, dxjdt = Wi 4- an2x2 + ••• + ann * n + bjt. Где xi x2 и xn — координаты, которые характеризуют работу системы. Система уравнений n (6.1) легко описывается в матричной форме. (6.2) dx / dt = Hell: + B /, где A — квадратная матрица коэффициентов вида a11 fl12 ~ ‘a \ n ) / / / (ω)], где A (ω) — амплитудная характеристика, а φ (ω) — фазовая характеристика системы.
Построение амплитудных и фазовых характеристик на цифровом компьютере сводится к многократным вычислениям передаточной функции с использованием мнимого значения аргумента s = / co, за которым следует построение по модулю и аргументу. Функция arctgx является многозначной, и поскольку цифровой компьютер может легко получить только основные значения функции, основная трудность заключается в определении значения аргумента Φ (ω). Для вычисления cp (co) = arctg * можно использовать не только значения x ~ tg )], но и информацию о значении sincp. (Co); coscp (co), (etf (co) = V (co) / A (co); cos (p (cu) = (V (co) / y4 (co)]. ,
Функция φ (co) может быть напрямую рассчитана через (/ (co) и Y (co) с использованием arcsinl / (co) // 1 (o)). Людмила Фирмаль
Преимущество этого варианта (V (co) / £ / ( <о) Расчет), чтобы уменьшить риск переполнения разгрузочной сетки. При решении задач автоматизации проектирования системы вы можете предоставить вывод для печати или других устройств отображения. Выводит амплитудно-фазовые характеристики как в нормальном, так и в логарифмическом масштабе на плоттер или дисплей. Особенностью механического исследования в этом случае является печать параметров стабильности связи равной амплитуды и фазы. Линии с одинаковыми границами амплитуды и фазовой стабильности можно комбинировать с областями стабильности, построенными с различной стабильностью и вибрацией.
Этот подход очень эффективен, поскольку является частным случаем многокритериального исследования. Такие процедуры являются неотъемлемой частью проблемно-ориентированного компьютерного программного обеспечения, предназначенного для механического анализа и синтеза систем управления. 11-X, 2 … » 21 а, 2 — л. * agp = 0 (6,5) ни али- Отрицательная вещественная часть, то есть слева от мнимой оси на плоскости комплексной переменной X. (6.5) описывается в матричном формате A-XE | = 0. (6.6) Здесь и ниже. Е означает единичную матрицу 0 … 0 «E = 0 1 … O L N Где / = 1,2, …, n.
- Разложение определителя (6.5) в соответствии с известными правилами дает характеристическое уравнение n-го порядка для X. cf (L) = | A-XB | = a ^ «+ a {\ n ~ 1 + a2 \ n-2 4- •• + a ^ X + an = 0, (6.7) 0 0 … 1 Уравнение (6.6) называется характеристическим уравнением системы (6.2), а его корень K, (i-1, 2, …, n) является собственным значением (собственным значением) матрицы A. Сумма элементов на главной диагонали образует след. Матрица А, обозначенная SpA. Трассировка матрицы связана с собственными значениями следующим соотношением:
Затем применяется один из известных критериев устойчивости, или корень уравнения вычисляется непосредственно численными методами. Однако расширение детерминантов высшего порядка (6.5) на цифровых компьютерах и сокращение до характеристических полиномов связано с серьезными трудностями чисто вычислительных свойств.
Такая формулировка обычно учитывает эту проблему. Людмила Фирмаль
Особенно при компиляции программы для построения области определенного качества, при анализе большого количества точек в пространстве параметров, число различных из-за определенных функций матрицы, таких как вырождение (то есть исчезновение) промежуточных определителей Вам нужно разбираться со случаями, программа становится громоздкой и сложной. Существуют способы построения полиномов, на которые не влияет определенная функция, но они не учитывают накопленную ошибку при округлении, которая может привести к качественному искажению значения результата (стабильная система нестабильна Интерпретируется как бытие, и наоборот).
Давайте кратко рассмотрим существующие методы изучения устойчивости с точки зрения возможности размещения стабильности на компьютере. Раут-Гурвиц, Лиенар — Хорошо известные стандарты, такие как Шипар, А.В. Михайлов, Найквист, Ланцош, были созданы задолго до появления цифровых компьютеров, и, конечно, все они одинаково полезны для использования на цифровых компьютерах. Не то. Это ставит задачу оценки существующих стандартов с точки зрения реализации цифрового компьютера и изменения их для применения к спецификациям электронных цифровых машин. Схема расчета должна быть максимально простой.
И это модифицируется, чтобы получить несколько итераций одной и той же последовательности операций в процессе расчета (периодичность). Обеспечивает подготовку высокопериодических программ, которые требуют минимального машинного времени для достижения заданной точности. Предоставляет возможности управления, оценивает точность процесса решения проблем, проверяет ошибки на этапе подготовки решения и, если возможно, показывает результаты возможных ошибок, таких как округление и усечение (ограничение) Рекомендуется, чтобы вы могли оценить. Стандарт Рауса-Гурвица. Чтобы выявить определитель Гурвица, вы можете использовать методы главных элементов или другие методы (например, привести к треугольной форме).
В этом случае логическое условие критерия Гурвица соответствует структуре критерия Рауса. Построить определитель матрицы Гурвица из коэффициентов характеристического уравнения (aΦ0). я = 1, 2, ти-1. а, а9 а5 а7 …. a0 a2 a4 a6 …. 0 а, а3 а5 …. 0 а0 а2 а4 …. B ‘0 0 0.’. ».. но н- \ Чтобы переместить матрицу Гурвица в прямоугольный треугольник, выполните следующие основные преобразования: Мы вычитали элемент в первом ряду над ним из каждого элемента во втором ряду и умножали ранее cx = ajax. Вместо строки, содержащей элемент a ^ a ^ ^ c, получите строку, содержащую следующий элемент. 0b2b4be%, где b2 a2-c, a3; 64 = a4-cx5 \ bf = ab-c, a7 и т. Д.
Сделайте то же самое для остальных строк ниже. Затем вычтите элемент в преобразованном ряду над ним из элемента в третьем ряду преобразованной матрицы с помощью c2 = a, / a2 и повторите ту же операцию в нижнем ряду. Продолжайте процесс по той же схеме, пока n-й шаг не даст матрицу прямоугольного треугольника, эквивалентную исходной матрице. Поэтому мы имеем A „L, 2 L, s A.4- 0 A22 A23 0 0 A ss AJ4- 0 0 0 l44 … 0 0 0 0 …. А Как известно, определитель треугольной матрицы равен произведению основных диагональных элементов. Чтобы рассматриваемая система (6.7) была устойчивой,
Элементы A ,,, D2.2, A33, An_, n_ на главной диагонали определителя Dn_ были положительными (a0> 0). Если хотя бы один из диагональных элементов не является положительным, то условие Гурвица устойчивой системы не выполняется. В этой форме расчет соответствует схеме проектирования на основе Рауса. Описанная процедура позволяет анализировать устойчивость линейных систем с помощью электронной клавиатуры компьютера. Схема расчетов Routh предлагает значительную экономию вычислений, работа является равномерной, и гарантируется хорошая периодичность выполнения программы.
Расчеты выполняются только для действительных чисел, а стабильность определяется путем изменения знака полученного числа. Лиенард-Шипар стандарт. Одна из модификаций стандарта Рауса — Гурвица была предложена в 1914 году Лиенаром и Шипаром. Стандарт Лиенар-Шипар сформулирован следующим образом: a „> 0, ap_r> 0 ….. D,> 0, D3> 0, a> 0, a ^ X), …, D.g> 0, D4> 0, …, И „> 0, 0, 0 ….. D,> 0, D9> 0, …, ap> 0, ap_x> 0, ap_9> 0 ….. D2> 0, D4> 0 ….. Где D | D.gD3D4 — диагональный минор матрицы Гурвица. Учитывая D, = a, вышеуказанное условие может быть выражено как: Az «—» Ap-Ap> Ap 1 D3, D6, …, Al_2 ”a„ 1 ai a3, …, a_2, ap D2, A4, …, Aya_3, Art_, A. , D4, …, Al_3, D „_, > 0, }> 0,}> 0,> 0, Четный н > 0; «1, a2> a4, ..». 2 D „A5, …, D„ _z. Л -1 а2, а4, …. а „ d2, d4, … ”Lla ,, a3, …, ap_3, aya D3, D5, …, D„ _3, D „-1 a„ a3t …, „_3, art_i , Ap Do, D4, …, Dia-2, Dia > 0, 4 »•••»
Критерий Лиенара — Шипара должен удовлетворять примерно половине определяющего неравенства нормального критерия Гурвица. Частотные критерии. Несмотря на тенденцию широкого использования компьютеров в области анализа и синтеза автоматизированных систем, частотный метод, применяемый в машиностроении, не потерял своего значения. Внедрение цифровых компьютеров может иметь независимое значение, позволяя дизайнерам быстро получать ценную информацию при изучении множества различных комбинаций параметров (построение линий границ стабильности, которые являются модульными и синфазными) И вы можете распечатать их).
Так, например, в настройке машины с L-разделением критерий Михайлова может использоваться для выделения областей стабильности среди нескольких заявителей. Машинная реализация люков Neymark в форме, используемой для ручных расчетов, требует довольно сложной программы. При настройке метода амплитудно-фазовых характеристик в цифровом компьютере исследование проводится в соответствии с передаточной функцией. N T aQsn -f- a | Srt_1 -f —- M
Смотрите также:
Примеры решения задач по теории автоматического управления

