Оглавление:


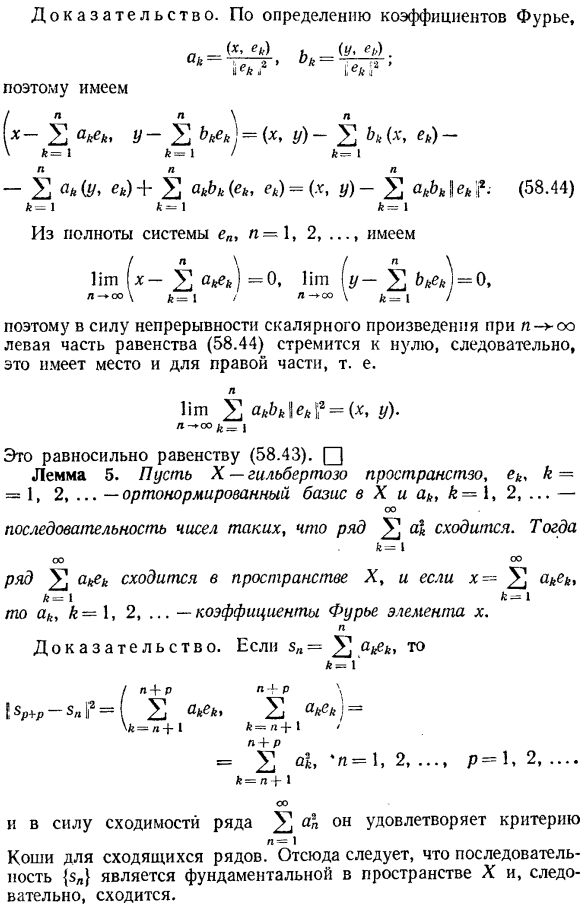





Существование базиса в сепарабельных гильбертовых пространствах. Изоморфизм сепарабельных гильбертовых пространств
Существование базиса в сепарабельных гильбертовых пространствах. Изоморфизм сепарабельных гильбертовых пространств. Теорема 9. Все сепарабельные линейные пространства X со скалярным произведением включают Slx-1, 2,…Есть ортогнатическая база. Доказательство. Если пространство X является N-мерным, то теорема очевидна (см. разделы 18.4 и 57.2). поэтому рассмотрим только, если пространство X является бесконечным измерением. 58.5.Наличие фундамента 49 г. Поскольку пространство X разделимо, оно содержит последовательность элементов Ф», 61 1, 2,…、 Образуют полную систему. Возвращает последовательность элементов путем непрерывного отбрасывания элементов, являющихся линейными комбинациями других элементов fi » 1, 2,…、 Он имеет тот же линейный диапазон, что и исходная система{φ»}, и линейно независим (причина).
Все сепарабельные бесконечномерные Гильбертовы пространства гомоморфны друг другу. Людмила Фирмаль
- Применение процесса ортогонализации (см. 58.2) и нормализации (см. 58.1) к результирующей системе дает ортонормированную систему. 1k* 1 = 1、^ = 1、2、…、 Он имеет тот же линейный корпус, что и система{fj}, поэтому он такой же, как и система{fn}.Из-за целостности системы этот линейный корпус плотен с X, поэтому система{en}является perfect. In в предыдущем разделе (см. комментарии после теоремы 7) было показано, что система элементов фронтального гильбертова пространства всех полных нормальных распределений является его основой. Тс Теорема 10. Сначала доказать 2 леммы. Первый из них обобщает равенство Парсеваля (58.35).
Лемма 4. X в гильбертово предпространство, ee (ep0)、 n-1, 2-Полная ортогональная система X, xeX, y / eX. И давайте посмотрим. И 2 БПВ л-1 л = 1 И затем… (Х, Y)= 2] Ану » 1е » Т (58.43) Н = 1 В частности, дальнейшее предположение| ee | / = 1, n = 1, 2 Да. (x, y) равно 2 л = 1 Выражение (58.43), очевидно, обобщает выражение скалярного произведения в конечномерном пространстве (см.§ 18.4). * Для определения бесконечномерного пространства см.§ 57.2, а для изоморфизма пространства см.§ 57.9 (определение 36). § 58.Регулярная основа и их развертывание 492. Proof. By определение коэффициентов Фурье、 (*ek) и (y, ek) АК-2 ″ БК ^〜 Х-2 АСК, г-2 БКК ’ \ =(Х, Y) > БК (х, ЕК) к = 1П к = 1 к = 1 ■2 АК (г, ЕК)+ 2 АФК (ЕК, ЕК)=(х, г) ^«/ а |! ЕС (58,44) А = 1 к = 1 к-1 N-1, 2, от целостности системы е…、 н / н Золото x-2nd^ * / =°1 t Y-2 M * = 0 л-ОО \ * = 1 / л-ОО В Г = 1 / Поэтому мы имеем.
- Итак, при непрерывности n-го скалярного произведения левая часть уравнения (58.44) стремится к нулю. Поэтому это относится и к правой стороне. П Золото 2 akk \ \ ek 1; 2 = ( * , y). л-о! Это эквивалентно равенству (58.43). Ноль Лемма 5. Пусть X-гильбертово пространство, ek, k = 1, 2,… ортонормированное основание X, ak, k = 1, 2,…Да. Серия 2] последовательность, в которой сходится st.И затем… B = 1 ОО ОО Линия 2 Если Akek сходится в пространстве X и x является Akek、 к-1 к = 1 ak, k-1, 2,… коэффициент Фурье x. П Доказательство. в случае zn = akSk、 к = р / Л + П Л + П 1®р+р-5л| / 2 =(2С1кСк, 2akeki = = «E&» = b 2-••••Р = 1. Два & = / г + 1° А при сходимости 2-й серии » она отвечает критериям Хмыкнул кори Сигер. Последовательность{zn}сходится, потому что она фундаментальна в пространстве X. 493. Позвольте мне. x =золото 8n, то есть ОО Н-1 58.5.
Наличие фундамента Тогда для единственности разложения пространственных элементов базиса (см. Примечание теоремы 7) (х, е)= В, П = 1, 2,…、 То есть использовать коэффициенты Фурье элемента x. Ts Доказательство теоремы 10.Пусть X и Y 2 сепарабельных бесконечномерных Гильбертовых пространства. Согласно теореме 9, Каждый из них имеет ортонормированный базис. en, n = 1, 2 и η= 1, 2 И Ф Е X и 2 в качестве точки доступа, и как Фурье Н = 1 И Элемент x, следовательно, по равенству Парсеваля, ряд n = 1 секунда Он сходится. введите Y = с}}.Согласно Лемме 5, это Н = 1 Значение. Отображение пространства X в пространство Y. В каждой с xex элемент, указанный элемент 1 / EY и реализует изоморфизм этих пространств.
На самом деле, в этой переписке, благодаря уникальности расширения базисных элементов, различных элементов пространства X соответствуют различные элементы из X. Людмила Фирмаль
- Кроме того, каждый элемент пространство y связан с некоторым элементом пространства X(то есть, на карте показана карта с космоса г). фактически, в случае y∈Y предполагается, что он расширяется до K в основании.、 г = 21 l = 1 секунда пусть X = 2 bnep(такой элемент существует. См. лемму 5). Н-1 Очевидно, что как только соответствие установлено, элемент x также соответствует элементу y. наконец, это соответствие указывает на то, что скалярное произведение сохраняется. Это вскоре следует из леммы 4. х = = 2 ап€N х-2 г-2 г-2 n-1 n-1 n-1 n-1 § 58.Регулярная основа и их развертывание 494. Благодаря этой Лемме И (х, х) −2] nn6l =(/, г). | | л = 1 Как модель гильбертова пространства.
Смотрите также:
Решение задач по математическому анализу

