Сущность метода интегрирования подстановкой заключается в том, что путем введения новой переменной удаётся свести заданный интеграл к новому интегралу, который является табличным.
В основе метода подстановки лежит формула замены переменной в неопределенном интеграле:
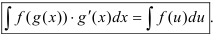
Для нахождения неопределенного интеграла методом подстановки (замены переменной) целесообразно использовать следующий алгоритм:
- Введите новую переменную
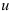таким образом, чтобы под знаком интеграла стояла функция, содержащая 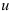(от этой функции должен существовать табличный интеграл), и производная 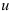. - Найдите
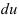по формуле: 
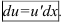. - Выразите
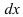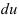через (при этом помните, что если множитель в одной части формулы находился в числителе, то в другую часть он перейдет в знаменатель и наоборот: если множитель находился в знаменателе, то в другую часть он «перейдёт» в числитель). - Подставьте 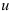и 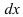в исходный интеграл. Если подстановка выполнена верно, то произойдет сокращение одинаковых множителей и интеграл сведется к табличному относительно переменной
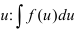. - Пользуясь таблицей неопределённых интегралов, возьмите полученный интеграл с переменной .
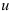- Перейдите от переменной интегрирования и к исходной переменной
.
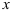Рассмотрим применение метода подстановки на конкретных примерах.
Пример решения заказа контрольной работы №65.
Найдите
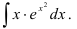
Решение:
1. Выполним подстановку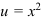 
с целью прийти к интегралу от функции 
.
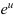Найдем 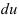по формуле
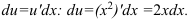
Выразим 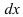из выражения пункта 2
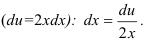
Подставим 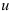и 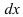в исходный интеграл:
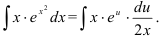
Видим, что переменную 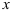можно сократить и прийти к интегралу относительно переменной и:
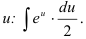
Для нахождения полученного интеграла константу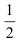 
вынесем за знак интеграла: 
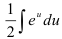По таблице неопределенных интегралов находим, что 
.
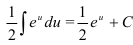Поскольку
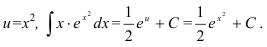
Ответ:
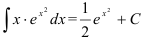
На этой странице вы сможете заказать контрольную работу и познакомиться с теорией и другими примерами решения:
Заказать контрольную работу по высшей математике
Другие похожие примеры возможно вам будут полезны:
