Оглавление:
Существенно особая точка
Если 
— существенно особая точка, то, как доказывается (теорема Сохоцкого-Вейерштрасса), в достаточно малой окрестности точки функция 
становится неопределенной. В такой точке аналитическая функция не имеет ни конечного, ни бесконечного предела. Выбирая различные последовательности точек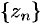 
, сходящихся к существенно особой точке , можно получать различные последовательности соответствующих значений функций, сходящиеся к различным пределам.
Пример №76.6.
Определить тип особенности функции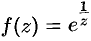 
в точке 
.
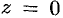Решение:
Функция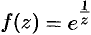 
в окрестности точки 
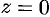имеет следующее лорановское разложение: 
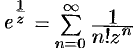(см. пример 76.4). Точка 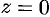является существенно особой точкой. Если 
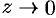вдоль положительной части действительной оси, то 
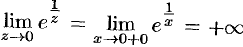; если 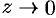вдоль отрицательной части действительной оси, то 
.
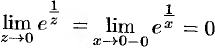Замечание. Классификацию изолированных особых точек можно распространить на случай, когда особой точкой функции является бесконечно удаленная точка,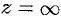 
.
Окрестностью точки 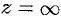называют внешности какого-либо круга с центром в точке 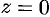и достаточно большим радиусом 
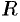(чем больше 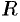, тем меньше окрестность точки ).
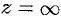Точку 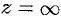называют изолированной особой точкой, если в некоторой окрестности ее нет других особых точек функции .
Бесконечно удаленная изолированная особая точка может оказаться устранимой особой точкой, полюсом порядка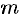 
или существенно особой точкой. В первом случае лорановское разложение функции в окрестности точки 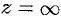не имеет членов с положительными показателями, во втором — имеет их лишь конечное число, в третьем случае в разложении имеется бесконечно много членов с положительными показателями.
Изучение функции в окрестности точки 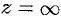можно свести путем подстановки 
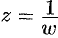к изучению функции 
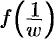в окрестности точки .
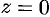Пример №76.7.
Найти особые точки функции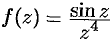 
.
Решение:
Особой точкой функции является 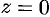. Найдем предел функции при : 
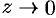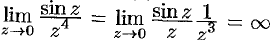. Следовательно, точка 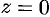является полюсом. Можно убедиться, что 
, 
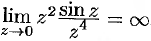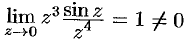. Следовательно (см. (76.17)), точка 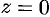— полюс третьего порядка.
Пример №76.8.
Исследовать особенности функции
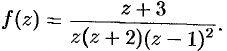
Решение:
Для данной функции точк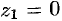и 
и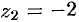 
— простые полюсы, 
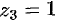— полюс второго порядка.
Пример №76.9.
Выяснить поведение функций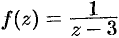 
, 
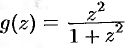в окрестности точки .
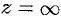Решение:
Сделаем подстановку 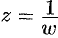. Тогда функция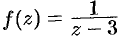 
примет вид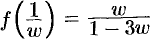 
. При условии 
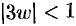имеет место разложение 
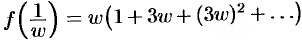. Возвращаясь к старой переменной, имеем
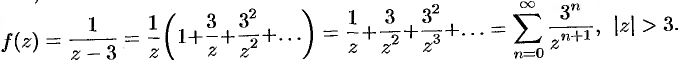
Поэтому точка 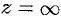является устранимой особой точкой (см. последнее замечание).
Можно убедиться, что 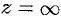для функции 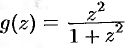является правильной точкой.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Классификация особых точек. Связь между нулем и полюсом функции |
| Устранимые особые точки |
| Вычисление вычетов. Применение вычетов в вычислении интегралов |
| Свойства преобразования Лапласа |
