Оглавление:






Субстанциальная производная
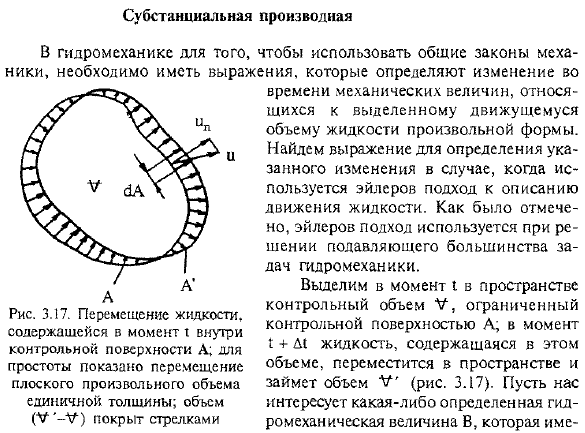
Субстанциальная производная. В гидродинамике, чтобы использовать общие законы механики, нужна формула, которая определяет изменение. Время механической величины, связанной с выбранным подвижным телом изделия любой формы текучей среды. Если вы используете подход Эйлера для описания движения жидкости, вы найдете формулу для определения изменения indicated. As упомянутый ранее подход Эйлера используется для решения большинства гидродинамических задач. В момент I в пространстве выберите управляющий объем V, ограниченный управляющей поверхностью A. At в момент X-r D1 жидкость, содержащаяся в этом объеме, перемещается в пространстве и занимает объем V ’(рис.3.17).
Он может быть скалярным (плотность жидкости и т. д.), векторным (скорость жидкости, плотность импульса), или тензором. Линии рассуждений будут те же самые. Людмила Фирмаль
- Остановимся на конкретной гидродинамической величине B с плотностью распределения p. это общий случай, он зависит от координат и времени. {3-p (r, 1). Рассмотрим производную по времени от указанной величины, связанную с общим объемом V. Из B= {при перемещении включаются Внутренне он является текучим в пространстве, имея в виду, что p является переменной Эйлера. Эта производная называется вещественной производной и обозначается OD) n. Преобразуйте одну и ту же правую часть уравнения, выполняя сложение и вычитание в числителе|. p (g, 1) нет.
В первом пределе Интеграл вычисляется в одном и том же объеме V’, а переменная X изменяется на 1-й раз X, следовательно, она вычисляется в один и тот же момент I, но для разных объемов V ’и V числитель вычисляется в разности (V’ 〜V) этих объемов, которая может быть выражена как 1 Интеграл. вы можете сделать это с помощью: Интеграл / p (g, g) bU это «количество» количества Объем (V «-V) (см. рис. 3.17); это»количество»осуществляется в DW при движении жидкости через поверхность и может быть рассчитана следующим образом: разделить контроль поверхности в базовой области 6А и построить его в качестве основы, каждый 1А представляет собой прямоугольный параллелепипед, окруженный сверху поверхностью а (рис. 3.18).
- Очевидно, что сочетание всех этих призм образует объем. Каждая Призма равна расстоянию между временем L! Поверхность A удаляется из A, а A перемещается из геометрической структуры, показанной на рисунке 1, поскольку она перемещается движением жидкости со скоростью U. 3.18、 Шестьдесят девять Значение высоты (un-A! Так и будет).Объем базовой призмы равен (un-Am) eA, а величина характеристики B внутри этой призмы может быть выражена в виде p (un-D ^ eA), что обусловлено фундаментальной природой объема. Рассматриваемый Интеграл представляет собой изменение характеристики B в результате протекания жидкости через управляющую поверхность A, в которой скорость жидкости определяется из управляющего объема, в части A (рис. 3.18,а) поток жидкости вводит характеристику B в объем (Y’d1-V); в этом случае p (IP) dL>0.
In часть а (рис. 3.18.5), которая направлена внутрь объема V, поток жидкости несет характеристику B от объема (V ’-V), p (ipD1) 0А0, поэтому необходимо учитывать выражение количества основной призмы в следующем виде: Необходимо учитывать знак un каждого элемента поверхности eA. Найти величину характеристики B объема (U’-U), суммируя величину этой характеристики во всех построенных базовых призмах. Подставляя это равенство в оставшийся нерасчитанный предел (3.48)、 Подставляя (3.50) в (3.48), получаем основную формулу субстантивной производной. Первый Интеграл справа представляет собой изменение гидродинамической величины B, связанное с объемом V, связанным с изменением 70.
Интеграл представляет собой изменение во времени одной и той же величины B, связанное с движением (переносом, конвекцией) в пространстве жидкости, содержащейся в моменте r в плоскости управления A, и называется конвективной составляющей вещественного дифференциала. Людмила Фирмаль
- Таким образом, во времени величина p (rd) в каждой точке объема V называется локальной составляющей вещественной производной. 2-й Используется для расчета поверхности area. It представляет собой конвективную составляющую существенной производной, формулу остроглацкого-Гаусса в виде: Если вы назначаете (3.52) на (3.51). Первый Интеграл в правой части (3.54)определяет вклад в существенную производную от| pa ^, обусловленный изменением. Р маска. Это, с другой стороны, локальное изменение, временное изменение этой величины в фиксированной точке пространства a (Я-Egaa) п С другой стороны, изменение Р обусловлено наличием трансмиссии (конвекции)、 Это связано с тем, что уравнение (и• & gai) p вытекает из интеграла (3.50), который определяет конвективную составляющую существенной производной B. 2-й Интеграл из (3.54) представляет собой существенный вклад в производную из-за изменения пространства.

