Оглавление:















Структурные схемы, уравнения и частотные характеристики стационарных линейных систем
- Структурные схемы, уравнения и частотные характеристики стационарных линейных систем Структурная схема в теории автоматического управления представляет собой графическое представление математической модели системы автоматического управления в виде блока связи. Структурные ссылки обычно указываются в виде прямоугольников с входными и выходными величинами и их внутренними передаточными функциями. Уравнение или характеристика могут быть показаны вместо передаточной функции.
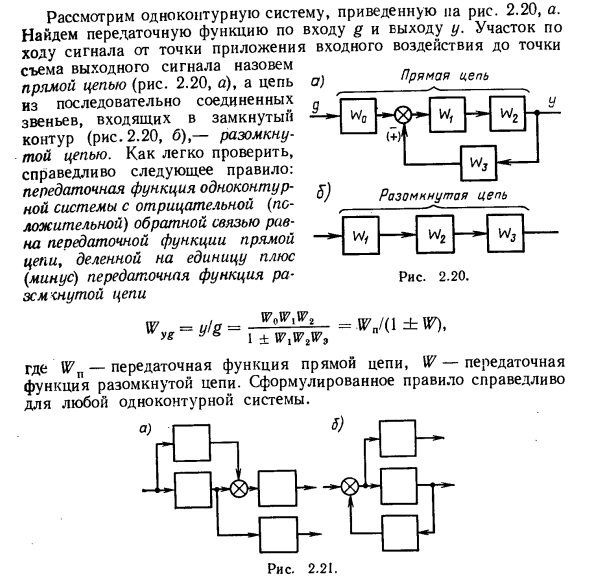
Вы можете нумеровать и передавать ссылки. Рассмотрим одноконтурную систему, показанную на рисунке. 2.20 а. Найдите передаточную функцию с входом g и выходом y. Участок вдоль пути прохождения сигнала от точки приложения входного действия до точки приема выходного сигнала называется прямой цепью (рис. 2.20, о) и представляет собой цепочку последовательно соединенных звеньев, содержащихся в замкнутой цепи (рис. 2.20, б) называется разомкнутой цепью.
Легко убедиться, что соблюдаются следующие правила: одноконтурная передаточная функция Прямая цепь А / Вт 1л / w0 О) 9. 1 W Разомкнутая цепь W, w2 Рисунок 2.20. ■ mil fti ^ mo t / c / ltsc / pltdlkil! // ил. «» Людмила Фирмаль
Передаточная функция системы с отрицательной (положительной) обратной связью равна прямой передаточной функции цепи, деленной на 1 плюс (минус) передаточной функции каждой микросхемы. -у, г = — W = Wa / (\ ± W). г 1 ± WxWtW9 Где Wn — передаточная функция прямой цепи, а W — передаточная функция разомкнутой цепи. Описанные правила действительны для одноконтурных систем.
Рисунок 2.21. Расчет передаточных функций для многоконтурных систем. Закрытая система (блок-схема) называется многоконтурной, если она становится цепью, содержащей параллель или обратную связь при открытии, в противном случае закрытая система, содержащая параллель в дополнение к локальной или основной обратной связи, называется многоконтурной. Она будет называться. Если обратная связь или параллельная петля покрывают часть схемы, которая включает в себя только начало или конец другой обратной связи или параллельной цепи, говорят, что многоконтурная система имеет перекрывающиеся звенья (Рисунок 2.21, a , Б).
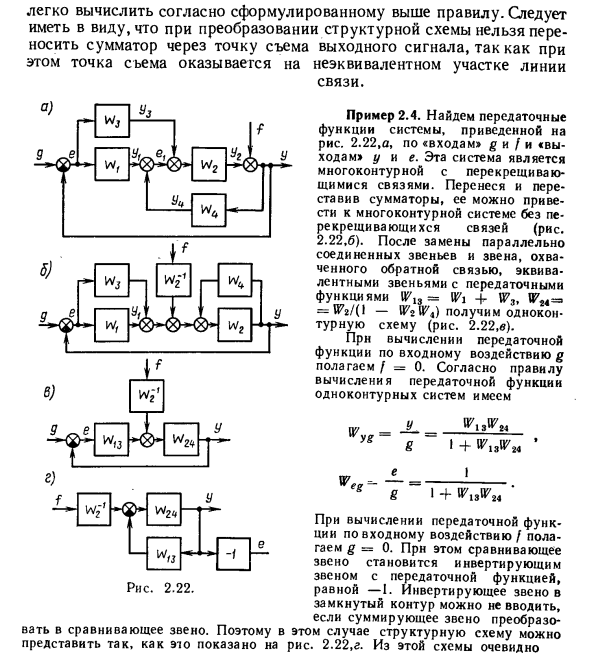
- Чтобы рассчитать передаточную функцию многоконтурной системы, сначала необходимо уменьшить перекрестную связь, переместив и перенеся узлы и сумматоры. Передаточная функция затем преобразуется в одноконтурную систему с использованием первых трех правил для преобразования структурной схемы. Вы можете легко рассчитать по правилам выше. Обратите внимание, что при преобразовании структурной схемы невозможно передать сумматор через точку срабатывания выходного сигнала. Это потому, что было обнаружено, что точка захвата находится в неэквивалентной части линии. Связь. «Z Uz В] W W »W2 — ^> 1? * б) C) 11 Wj «Mr. GK о * -1 W
Найдите передаточную функцию для системы, показанной в примере 2.4. С 2.22, a, «входом» g и / или «выходом» y и e, эта система является многоконтурной кросс-коммутацией. Перемещая и перемещая сумматор, он может быть преобразован в многоконтурную систему без перекрестных соединений (рисунок 2.22.6). Замена ссылки, соединенной параллельно, и ссылки, покрытой обратной связью, эквивалентной ссылкой с передаточной функцией Wl3 »Wi + W3, = №r / (1-WtWx) дает одноцепную схему ( Рисунок 2.22, в).
Установите / = 0 при расчете передаточной функции от действия ввода g. Согласно правилам расчета передаточной функции одноцепной системы, W _ _ Y 8-а Я + T W2 «U -1 I — s -1> -i Людмила Фирмаль
Рисунок 2.22. ! г) 1 + ^ 18 * 24 Установите g = 0 при расчете передаточной функции из действия ввода. Следовательно, ссылка сравнения является инвертированной ссылкой с передаточной функцией, равной -I. Если ссылка суммирования преобразуется в ссылку сравнения, инвертированная ссылка в замкнутом контуре может быть опущена. Следовательно, в этом случае структурная схема может быть представлена так, как показано на рисунке. 2,22 г. Это ясно из этой цифры
y e Sff, ————-_. Y / / \ + Wu * it » f l + Mis С помощью передаточной функции системы дифференциальных уравнений нетрудно записать дифференциальное уравнение. Если система имеет одну контролируемую переменную, для полного объяснения достаточно одного дифференциального уравнения, представляющего взаимосвязь между выходом и входом. Автоматизированная система с одной контролируемой переменной называется одномерной автоматизированной системой. В общем случае дифференциальное уравнение одномерной системы с двумя входными величинами имеет вид
Например, поведение вождения и тревожное поведение / (A) {n-I) (м) (m-I) aQy + i, y 4- ••• + ад = + bt g H —- + b „g + (0 (/ -o + s J + s, / + •. + S J. Получите дифференциальное уравнение для системы, изученной в примере 2.4 (рис. 2.22, а). Вы можете написать для нее Y = «V + Wyff. (2,53) Это символическое дифференциальное уравнение, которое связывает выходную величину y с входной величиной. Аналогично, дифференциальные уравнения могут быть записаны для других «выходных» величин. Основываясь на определении передаточной функции, вы можете легко перейти от формулы (2.53) к обычной «несимвольной» форме записи. Например, = K-V (P + 1). W9 = k9 / p, W, = kk. тогда • W = + 1 w = k (p2 -> — / ») • tu + 7> + I ‘y / ry + 7 ^ + 1 * = 1 / (^ s), r, = KF, rt = (1-f-te = Ar, / ^,. Поэтому, основываясь на (2.53), мы можем написать: Tli’y + Tty + y = T9g + g + * (‘/ + /).
Частотные характеристики. При исследовании и проектировании автоматизированных систем обычно используются амплитудно-фазовые (AFC) и логарифмические (LFC) частотные характеристики открытой системы. Открытые одноконтурные и иногда многопетлевые числа передаточных функций могут быть легко преобразованы. Частотные характеристики. При исследовании и проектировании автоматизированных систем обычно используются амплитудно-фазовые (AFC) и логарифмические (LFC) частотные характеристики открытой системы.
Открытые одноконтурные и иногда многопетлевые числа передаточных функций могут быть легко преобразованы. W (s) = fl ^ (s), (2,54) Где Wt (s) — основная функция передачи ссылки. В этом случае модуль и аргумент частотной передаточной функции системы из n звеньев M <) = | ^ (ложь) |, Λ, (>>) = | Гм / с) |,
) • я = я Реальные и мнимые частотные функции системы определены равенство U (co) = A (co) cos ] Где L (w) и Li ((d) — логарифмические амплитудно-частотные функции, и по определению L (ω) = 201 bA (>) )) это. Из (2.56) и (2.58) следуйте следующим правилам для построения системы LF (LACH и LPC), в которой передаточная функция преобразуется в формат (2.54): Добавить графически. На основе (2.58) также может быть разработана несколько другая и более простая процедура для построения LAHF.
Сначала приведен конкретный пример. LGO) -60 дБ / дек -20 дБ / дек Рисунок 2.23. (2,57) 100 (с-ч я) U7 (s) = Зв (10S + 1) (0,01 секунды + 0,1 секунды + 1) Лог амплитудно-частотная функция L (ω) = 40-v 20 logо) -20 log | / «(10 <о) * + 1 -f 20 log ^ (^» TT- -20 log V (I-0,0 1g> ‘) 2 -f (0,1®))’ g. Асимптотическая ЛАФ рассматриваемой системы состоит из четырех асимптот (рис. 2.23, а, б, в) и имеет следующую структуру. Рассчитать частоту спаривания ω = 1/10 = 0,1, <o2 = 1, © 3 = 1 / 0,1 = 10.
Где cot, © 4 и © 3 — сопряженные частоты апериодических, вынужденных и колебательных связей соответственно. При построении асимптотического LAF основного звена на частоте ниже, чем частота сопряженного, под корнем остается только один (игнорируется оставшимися членами), а на частотах выше, чем частота сопряженного элемента, член наивысшей степени © Останется. Итак, в рассматриваемом примере для © <©, L (©) «40-в 20 log s. Это первое асимптотическое уравнение. Согласно этому уравнению первая асимптота рисуется с градиентом v20 дБ / дек от точки с координатами © = 1 и L = 20lgfc.
Закончите на первой частоте спаривания. cjj <© <(Если 0,2, то же самое , Z, (со) до 40-v 20 log (o-20! G 10 © = 20-v20 log co-20 log ©. Это уравнение асимптотическое. Наклон изменяется на –20 дБ / дек и обусловлен апериодической связью. Вторая асимптота выполняется от конца первой асимптоты до второй сопряженной частоты с наклоном — (- v-20-20) дБ / дек в соответствии с уравнением. Когда © 2 s © <© s L (©) »20-v 20 log © -20 log co + 20 log © = 20-v • 20 log ©. Это третье асимптотическое уравнение. Наклон изменяется на 20 дБ / декабрь и определяется усилением линии. Третья асимптота проходит от конца второй асимптоты до третьей частоты сопряжения с наклоном -v-20 дБ / дек. ©> © s L (©) = 20-v. 20 log © -40 log 0.1 © = 60-v. 20 LG © —40 LG ©. Это последнее четвертое выражение asnmptogi.
Наклон изменяется на –40 дБ / дек относительно третьей асимптоты и вызывается вибрирующим звеном. Легко сформулировать общие правила построения асимптотических LAF-систем с передаточными функциями вида W (s) = f] Wl (s), (-1 Где tt ^ (s) — основная функция передачи ссылки. Правила построения асимптотического LACH. 1. Частота спаривания и значение 20Ig & рассчитываются. Где k — коэффициент передачи системы, равный произведению N Точный коэффициент связи k = P ! т \ 2. Постройте первую асимптогу, которая работает на первой частоте спаривания через точки с координатами co = 1 и L = 201g k. Функции, уравнения или свойства отображаются вне структурной схемы.
Если передаточная функция указана в виде изображения, входные и выходные значения записываются в виде изображения. Однако гели и передаточные функции указываются в форме оператора, или ссылки описываются в дифференциальных уравнениях, а входные и выходные переменные записываются в их первоначальном виде. Ссылки и дополнения (рис. 2.13, б) Ссылки изображены в виде кружков, разделенных на сектора. В линии сравнения сектор, в который поставляется «франшиза», темный (рис. 2.13, б) или Поставьте знак минус перед соответствующим входом (рис. 2.13, а).
Структурные схемы широко используются в исследованиях и разработках автоматизированных систем управления для визуального представления соединений, транзитов и преобразования сигналов между системами. В математических объяснениях автоматизированная система обычно рисуется в форме блок-схемы, а уравнение для каждого «блока» (элемента) записывается на основе физических законов, которым следует система. Блок-схема может быть создана на основе этой блок-схемы и полученного уравнения или только на основе последнего. А дополнительные преобразования, необходимые для получения системных уравнений и передаточных функций, проще и нагляднее выполнять в соответствии со структурной диаграммой.
Структурные ссылки ссылок не обязательно представляют модель отдельного элемента. Это часть модели элемента, комбинации элементов или общей системы. Основные правила преобразования структурных диаграмм. 1. Соедините последовательное соединение (рисунок 2.14, а). При последовательном соединении каждое предыдущее выходное значение «\ y = y, + y2 Рисунок 2.13. Ts U, Ug Up; «n pack w w» Рисунок 2.14. Наклон — v20 дБ / дек. Где v равно разнице между количеством интегрированных ссылок и дифференцированных ссылок. 3. Используйте вторую асимптоту от конца первой асимптоты до второй частоты сопряжения.
Наклон изменяется на 20, -20,40 или -40 дБ / дек, в зависимости от того, является ли это повышающей, апериодической, повышающей частотой сопряжения второго порядка или колеблющейся линии связи соответственно. 4. Как и во втором, постройте каждую последующую асимптоту. Изменение наклона (<+1) -й асимптоты зависит от частоты сопряжения, на которой основным элементом является coj. Если имеется несколько сопряженных частот и их кратность равна /, то есть существует одна и та же базовая единица /, то изменение наклона на этой частоте будет / в разы больше, чем на соответствующей простой частоте.
Для звеньев вибрации с низким коэффициентом демпфирования (£ <0,4) асимптотический LAFC должен быть скорректирован по частоте спаривания с использованием точной формулы или кривой коррекции (рис. 2.9, d). ссылка является входом для следующей ссылки. При преобразовании структурной схемы цепочка последовательно соединенных звеньев имеет одно звено, номер (ы) передаточной функции которого равен произведению передаточных функций отдельных звеньев W (s) = ПWt (s) (рисунок 2.14.6). вы можете заменить).
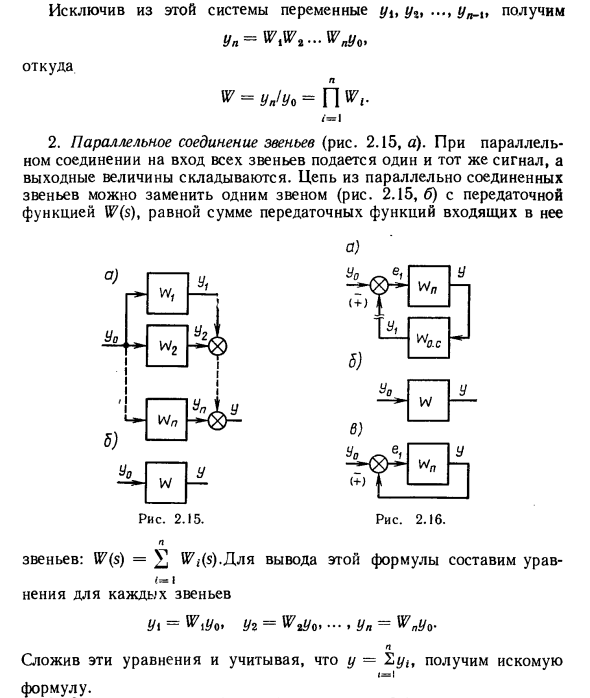
Написать уравнение связи Yx = y, = ^ mUx ….. yn = ^ nUn-x • Если вы удалите переменную yi yit y „_tt из этой системы, yn = WtWt … W ^ O, Откуда * = Y J Y «= P» V 2. Параллельное соединение звеньев (рис. 2.15, а). При параллельном соединении один и тот же сигнал вводится во все ссылки, и выходные значения добавляются. Цепочка звеньев, соединенных параллельно, может быть заменена одним звеном (рис. 2.15, б), равным сумме передаточных функций, включая передаточную функцию W (s) t а) W Рисунок 2.15. «0.C Вы есть e1 Wn Рисунок 2.16. вес (+) J И / 5) с)
Ссылка: Нет. (S) = V Нет., • ($). Создать уравнение для получения этого выражения Все ссылки ссылки Y \ = Wty9, yy = ….. yn = UYpu0. N Добавьте эти уравнения и учтите, что y = 2yt, чтобы получить искомое выражение. 3. Ссылка подлежит обратной связи (рис. 2.16, а). Общепринято, что когда выходной сигнал подается на вход через другую ссылку, ссылка покрывается обратной связью. Кроме того, если сигнал обратной связи yx вычитается из входного действия y0 (et ~ y0- * /,), обратная связь называется отрицательной. Если сигнал обратной связи yx объединяется с входным действием y0 (et = Y0 — \ — y )%, обратная связь называется положительной. Откройте отзыв перед ссылкой сравнения (рис. 2.16, а).
Тогда вы получите цепочку из двух последовательных соединений Link. Следовательно, передаточная функция W открывает fns. 2.16, а) равно произведению прямой передаточной функции W и передаточной функции Wo с обратной связью: W —WaWQ C Передаточная функция ^ W ^ wwwymouj ^ nuj: .. Отрицательный … Обратная связь -Ссылка возвращена к отрицательному 11.link <x, -Это равно передаточной функции прямой линии, деленной на единицу плюс цикл Функция петли, чтобы разомкнуть цепь = Wn / (\ -f W). Чтобы вывести это уравнение, запишите уравнение для каждой ссылки Y = UV; y r = W0.eyte {= y0-yy.
В этой системе последнее уравнение — уравнение линии сравнения — называется уравнением замыкания. Исключение переменных ex и yh из упрощенной системы приводит к уравнению y = Wu (y0-Wocy) или (1 + Wu Wo c) y = Wny0. Отсюда — Да! Y o = WJi + WnW0, c) = WJ (\ + П Аналогично, если отзыв положительный Передаточная функция с обратной связью с положительной обратной связью равна передаточной функции прямой цепи, деленной на 1 минус передаточная функция с открытой цепью. Когда передаточная функция № 0.s = 1, обратная связь называется единицей, и структурная схема рисуется, как показано. 2.16, е.
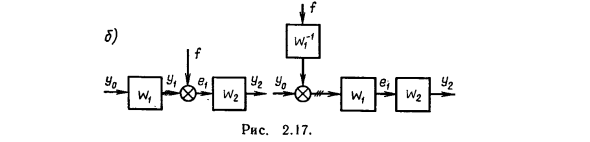
Передаточная функция W3 в этом случае принимает вид W3-WJ (1 -fпn) с отрицательной обратной связью и = n n / (l-Wn) -положительной обратной связью. При преобразовании структурной схемы сумматоры и узлы должны быть перенесены и перемещены. В этом случае подумайте, какие изменения необходимо внести в схему. 4. Движение сумматора (рисунок 2.17). Если вы передаете сумматор вдоль сигнала, легко показать, что вам нужно добавить следующую ссылку. Я Ву Ву IV, «г А /» г Святой вес Рисунок 2.17. Точная функция равна передаточной функции ссылки, на которую передается сумматор (рис. 2.17, а).
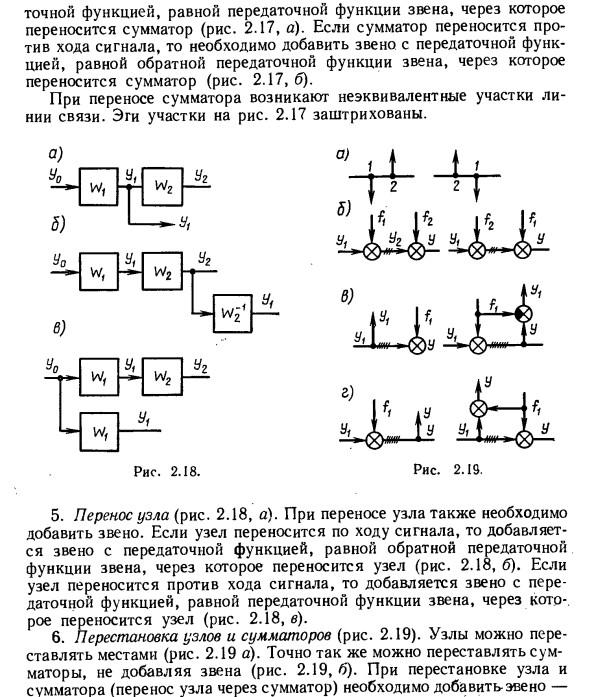
Если сумматор передается выше по потоку от сигнала, необходимо добавить ссылку с передаточной функцией, равной обратной функции пересылки ссылки, на которую передается сумматор (рис. 2.17, б). Передача сумматора приводит к неравному участку линии связи. Пример 2.17 на рисунке заштрихован. да о) у ± 5) ч с) Рисунок 2.19. да W W W вес да да -1 да W U1 W Рисунок 2.18. 5. Переадресация узлов (рис. 2.18, а). Если вы переносите узлы, вы также должны добавить ссылки. Когда узел передается по сигналу, добавляется ссылка с передаточной функцией, равной обратной функции передачи канала, на который передается узел (рис. 2.18, б).
Если узел передается выше по потоку от сигнала, добавляется канал с передаточной функцией, равной передаточной функции канала, на который передается узел (рис. 2.18, в). 6. Перемещение узлов и сумматоров (рисунок 2.19). Узлы могут быть перемещены (рисунок 2.19a). Аналогично, сумматоры можно переставлять без добавления ссылок (рисунок 2.19.6). При перемещении узлов и сумматоров (пересылка узлов через сумматоры) необходимо добавить ссылки.
Резюме или сравнение (рис. 2.19, в, г). При передаче узла через сумматор и при перемещении сумматора возникает неравный участок линии связи. Эти области заштрихованы на рисунке. Расчет передаточных функций для одноконтурных систем. Замкнутая система (блок-схема) называется одиночной цепью, если при ее открытии в какой-то момент вы получаете цепочку последовательно соединенных звеньев или схему, которая не включает параллельные соединения и соединения обратной связи.
Смотрите также:
Решение задач по теории автоматического управления
| Выбор параметров по минимуму интегральной оценки | Многомерные стационарные линейные системы |
| Выбор параметров н синтез корректирующих устройств ио корневым годографам | Нестационарные линейные системы |

