Оглавление:






Стоячие колебания в каналах переменной глубины
Теория стоячих волн на жидкости определенной глубины была. Пример из гидромеханики, он ограничен длинноволновым случаем и показывает, как определяются установившиеся колебания жидкости, ограниченной сосудом, дно которого не является горизонтальным. Этот последний случай происходит, например, против Сейша, который возникает в озере и представляет собой свободное колебание всей жидкости в озере.
Мы видим, что уравнение свободной вибрации жидкости удовлетворяет следующему уравнению, если сначала поместить исключение в последнее уравнение. Теперь рассмотрим плоское движение в канале, где дно имеет параболическую форму, так как глубина представлена уравнением. Если длина озера, которая является максимальной глубиной озера (ширина в направлении оси не играет никакой роли в рассматриваемом движении и может быть принята за единицу), очевидна.
- Для учета в каналах постоянной глубины установившихся колебаний жидкости мы делаем следующее. Чтобы определить из последнего уравнения, получим уравнение.
- Для простоты введем новую переменную. Далее, для определения.
Итак, если левая сторона уравнения исчезает, то правая сторона, то есть форма уравнения, указывает на то, что можно найти решение этого уравнения в виде полинома степени. Людмила Фирмаль
Условие делит этот многочлен. Тестируйте полиномы, такие как и порядок, непрерывно.
Для полинома порядка, это. Это объясняется тем, что линейность уравнения может отличаться только от постоянного коэффициента, который не играет никакой роли. И для того, чтобы уравнение было выполнено, человек должен принять.
- Это уравнение в цилиндрическом сосуде малой глубины определяет период колебаний. Найдите тип профиля формы волны.
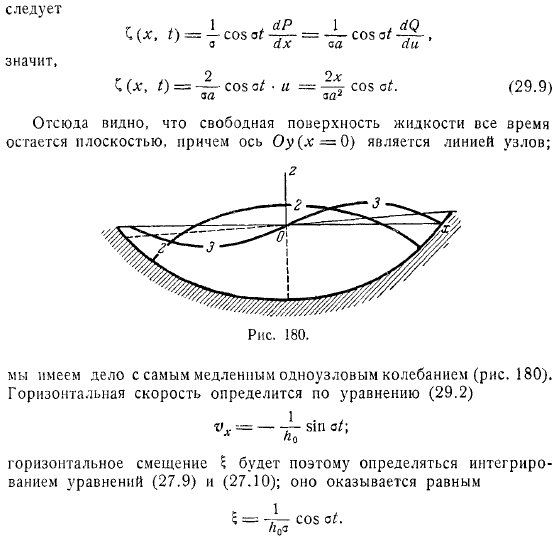
- Это указывает на то, что свободная поверхность жидкости всегда плоская, а ось является линией узла. Он имеет дело с самыми медленными одноузловыми колебаниями.
Горизонтальная скорость определяется уравнением, и поэтому горизонтальное перемещение определяется путем интегрирования. Оказывается, равны. Таким образом, вся масса жидкости колеблется из стороны в сторону, совершая гармонические колебания с амплитудой.
Для полинома порядка его делимость позволяет принять следующий. Людмила Фирмаль
Поэтому мы должны принять. Период колебаний выглядит следующим образом. Профиль волны является. Вторичная парабола. Есть секции. Аналогично, колебания типа узел, узел и т. д.
Ожидаются, но период этих колебаний постепенно сокращается, и законы их изменения заключаются в следующем. Он показывает примерную продолжительность Сейша. Ширина и глубина озера Лемерск составляет около минуты, но есть Сейш, который пересекает за несколько минут.
По формуле это выглядит так. Самый продолжительный период (около нескольких часов) Сейша наблюдался в Аральском море. Аральское море длинное, неглубокое по глубине.

