Сторона поверхности

Оглавление:

Сторона поверхности

Боковая поверхность. Это важно для дальнейших выставок. В некоторых случаях это понятие интуитивно понятно. Если поверхность задана явным уравнением вида g=/(x, y), то можно говорить о е р х н е й стороне или о n и W Н Е Й стороне*) p. *) Обычно

такое выражение (имеется в виду, что сама ось 2 ориентирована перпендикулярно B E R x). Основываясь на этом интуитивном представлении, мы теперь попытаемся дать точное определение понятия поверхностной стороны.

Рассмотрим, является ли поверхность (5) замкнутой, и предположим, что каждая точка Людмила Фирмаль

поверхности имеет постоянную касательную плоскость и ее положение изменяется в точке контакта. Взяв определенную точку L4 на поверхности, мы рисуем нормаль к ней, на ней назначаем определенное направление—одно из двух возможных (они проведут замкнутый контур на поверхности, исходят из L40, возвращаются к 7I0, предполагают, что граница поверхности не является N e e e E, если

есть). Переместите точку M на этот контур и добавьте две точечные нормали к каждой из его последовательных позиций. Двусторонние 299 направление n o n e p R e r S проходит выбранное нами направление в первой позиции D40. После пересечения контура, либо вернуться к точке с нормалями в том же направлении, или построить

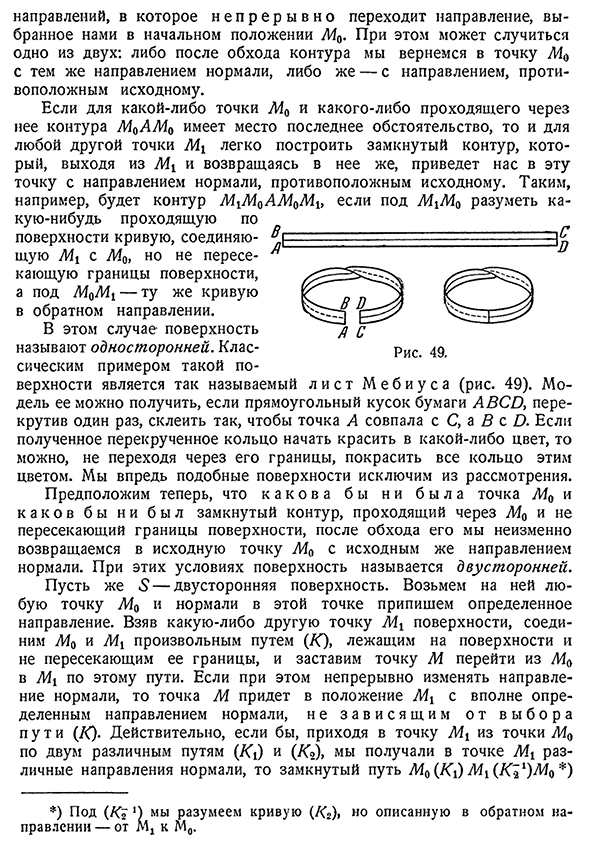
направление. В \ / г л и ст м е б и у С а (рис. 49). Mo- Противоположность оригиналу. В случае любой точки Mo и любого контура 7ioa7io,проходящего через нее, возникает последняя ситуация, когда другая точка MX строит замкнутый контур, который покидает MX и возвращается к нему таким,например, контуром mkhm0am0mkh.Если под Mkhm0 подразумевается любой проход по кривой поверхности, соединяющий MX с L40, но не пересекающий

границу В этом случае поверхность называется односторонней. Классический пример такой поверхности, прямоугольный лист бумаги АВСИ, один раз скрученный, если точка А совпадает с точкой С, А Е и с клеем, полученным в результате скручивания будущего, такая поверхность исключается из рассмотрения. Предположим теперь, что это было бы a to o to O также Lapointe Mo и o даже был бы замкнутый контур, не проходящий через граничную плоскость, и после обхода его при этих условиях поверхность называлась бы обеими сторонами. * 5 двусторонняя поверхность.

Возьмите любую точку L40 и нормали в этой точке и назначьте определенное направление. Возьмем другие точки поверхности MX, L40 и Людмила Фирмаль

M{соединяем любой путь (LE будет лежать на поверхности и не пересекать ее границы, точка m от L40 до MX на этом пути будет непрерывно менять направление нормали, если точка M придет в обратном направлении, то это не обычное конкретное направление MX, а голова и-от MH до Mo.300 главы ХХІІ поверхности. Поверхность Точка L40 находится в направлении, отличном от исходной нормали, и не согласуется с определением двусторонней поверхности. Поэтому на двусторонней поверхности выбор направления нормали в точке однозначно определяет выбор направления нормали во всех точках

поверхности. Совокупность всех точек поверхности с направлением, назначенным их нормали в соответствии с заданными правилами, и конкретным С Т О Р о н ы м О В Е Р х н. Пи-ли-МА 1) Самым простым и наиболее важным примером двусторонней поверхности является поверхность, представленная явным уравнением 2= = g (x, y), предполагающим, что функция 2 смежна с некоторой плоской областью (O), и что DH и%du ‘ одинаковы. В этом случае индуктивный Косинус нормали к поверхности задается формулой[n°213, (24)]: — П. Pop X= ——-= = = = , поп Р. — — — — — — — — — Я г , ± / 1+Р2+? От 2±до 1 + R2+? 3-1 (8) Установите определенное направление нормалей во всех точках

поверхности, выбрав определенный знак перед радикалами. Поскольку направляющий Косинус, по предположению, становится непрерывной функцией координат точки, установленное направление нормали также непрерывно зависит от положения точки. Следовательно, Соз х, сов Р, выбор предыдущего знака радикала формулы Соз н, в смысле, приписываемом вышеприведенному понятию, может определить с Т О Р О Н П О В Е В Н О С Т. Во всех отношениях поверхности, Выбирая знак плюс перед радикалом Один. Поп= » —- —— То есть угол, состоящий из оси 2 нормалей, соответствующей выбранной стороне, является ОС т ы м. таким образом, аспект поверхности определяется указанным выбором знака и находится на стороне е р х н е й. И наоборот, выделение отрицательных знаков в Формуле направляющего

Косинуса нормали не характеризует N-ю сторону поверхности.нормалей с О Ы г u2t ю н ы е углы. 2) здесь рассмотрим параметрические уравнения x=x (I, V), y=y (I, y), g=g (a, V), (Z) и вообще любую поверхность (5), заданную параметром. Мы предполагаем, что поверхность гладкая,то есть С и М и ч а с т н ы м и П О и Б О Д н ы м и Н О П О В Е Р х н е t362]§1. Двусторонняя поверхность 301 Для индуктивного Косинуса нормали к поверхности она имела формулу(7). И, в данном случае, выбор кода до того, как радикалы характеризуют с Т О Р О Н О В Е Р Х О С Т и, поверхность является у Т О Р о н е й д. Фактически, когда символ выбран, формула для каждой точки поверхности(7) (для d n a ответит только на одну пару

значений, поэтому g/!) Отображение одного конкретного направления нормалей, которые непрерывно меняются по мере движения точки. Если предположение о поверхности нарушается, то уже нельзя безоговорочно утверждать, что она двунаправлена. В этом случае существует точка поверхности Mo, соответствующая двум различным парам и и^значению параметра, и в этих значениях уравнения (7), Если это действительно верно до того, как радикалы будут выбраны одинаково, поверхность будет о д н о т о р о н е й. Если поверхность (5) замкнута и некоторые тела ограничены, то[n°360]может быть выражено уравнением (Для), но на этот раз точка поверхности и площадь поверхности (а), Однако, поскольку есть две стороны поверхности, то-в Н Е Н е й и в н е т е-В Р ясен, в этом случае (7) выбор знака

Аналогия с простым интегралом. Интеграл по ориентированной области	Ориентация поверхности и выбор ее стороны
Параметрическое представление поверхности	Случай кусочно-гладкой поверхности