Оглавление:



Стесненное кручение и его особенности
- Сдержанность скручивания и ее особенности Тесный, скрученный называется твист, который истощается на множество различных поперечных сечений. Например, если тонкостенный стержень
цилиндрический (см. Рисунок). 335, a) закройте один конец строго, и добавьте вращающий момент к другому концу, часть в уплотнении останется 394план (депланация равна нулю), максимум на
свободном конце секции депланации. Средняя секция изменяется по некоторым Людмила Фирмаль
законам от нуля на закрытом конце до максимума на свободном конце. Так как движение точек в разных частях по длине разное, то происходит относительное удлинение волокон (е=/=0), а в поперечном сечении стержня возникает не только тангенциальное, но и нормальное напряжение. Чтобы изучить основные особенности ограниченного кручения, рассмотрим двутавровую балку, плотно
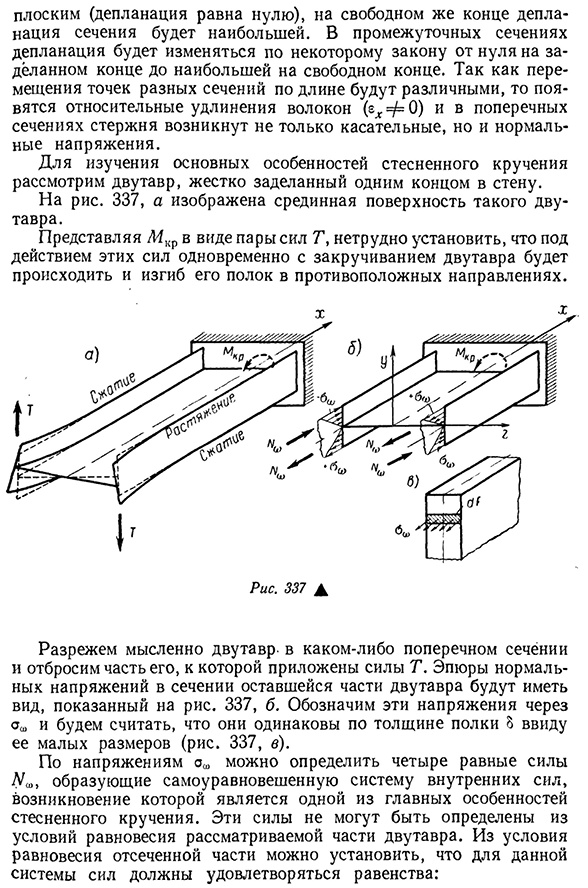
встроенную в один конец стены. Для риса. 337, и показывает среднюю грань такого I луча. Представляя L4kr в виде пары сил T, нетрудно установить, что под действием этих сил одновременно с закручиванием двутавровой балки ее полки изгибаются в противоположную сторону. Рис 337d Мысленно разрежьте двутавровую балку с произвольным поперечным сечением и отбросьте ту часть, где приложена сила т. График нормальных
- напряжений в оставшемся сечении двутавровой балки показан на рисунке. 337, б.обозначим эти напряжения и предположим, что толщина полки одинакова, учитывая ее малые размеры(рис. 337, в). По напряжению можно определить кватернионную силу, которая образует самобалансирующуюся систему внутренних сил, возникновение которых является одной из основных особенностей сдерживаемого скручивания. Эти силы не могут быть определены из состояния равновесия рассматриваемой части балки. Из состояния
равновесия отрезанной части можно установить, что для данной системы сил необходимо удовлетворять равенству: 395mg=У(Со, У=0;П (К,г)г=0;(13.6) N=[a. y R^O, R То есть изгибающий момент как для главной оси инерции, так и для продольных сил сечения должен быть равен нулю. Один. Рис 338А Тангенциальное напряжение также возникает в поперечном сечении. Поскольку и крутильная деформация, и изгибная деформация происходят одновременно, в результате в поперечном сечении стержня возникают две системы тангенциальных напряжений, соответствующих указанной деформации. Первое-это напряжение, которое распределяется в сечении по закону свободного (чистого) кручения.
Покажем эти напряжения t0, а соответствующий момент, через L40, назовем Людмила Фирмаль
моментом чистого кручения. Последнее можно представить как сумму моментов основной пары, составляющими которых являются тангенциальные силы, возникающие в сечении стержня (рис. 338, а). Определение напряжений t0 и соответствующих углов кручения осуществляется по формулам (13.1) и(13.2). Тангенциальное напряжение, связанное со второй системой, обозначается TS и возникает из-за того, что перпендикулярные напряжения O в поперечном сечении стержня не равны.. Направления напряжений двутавровых полок противоположны друг другу(рис. Этот момент приходит вместе с моментом mo уравновешивает внешний крутящий момент L1kr. Таким образом, внутренняя сила в поперечном сечении
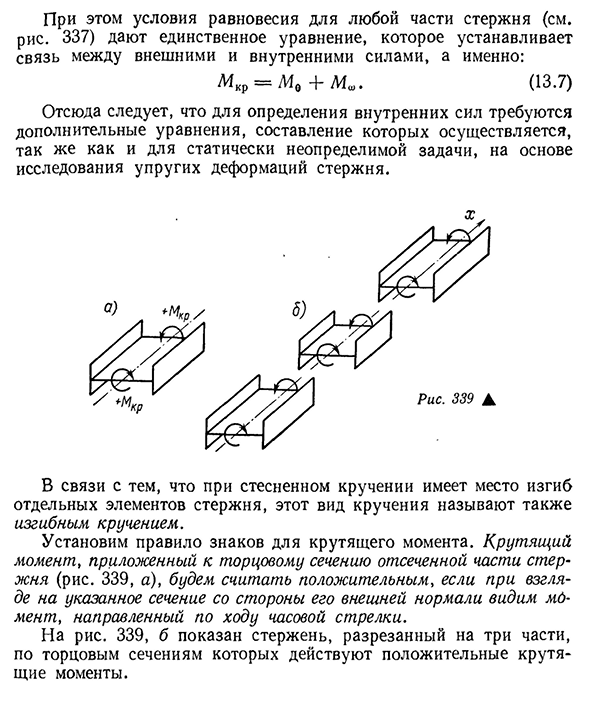
стержня при ограничении кручения, в момент чистого кручения М О и изгибающего момента, самонапряжения вертикальной силы связана с напряжением золы. 396 условие равновесия любой части стержня (см. 337) дает только одно уравнение, устанавливающее соотношение между внешними и внутренними силами: мкр-М0 4 — (13.7) оно основано на исследовании упругой деформации стержня для определения внутренних сил. Кручение такого типа также называют изгибным кручением, в связи с тем, что связывание
кручения создает изгиб отдельных элементов стержня. Устанавливает правило знака для крутящего момента. Крутящий момент, приложенный к концу отрезной части стержня (рис. 339, а), рассматривая указанное сечение с внешних нормалей, мы рассматриваем направление движения по часовой стрелке как положительное значение. Для риса. 339, b показывает стержень, который разрезан на три части, и его конец имеет положительный крутящий момент.
Смотрите также:

