Задача №1.
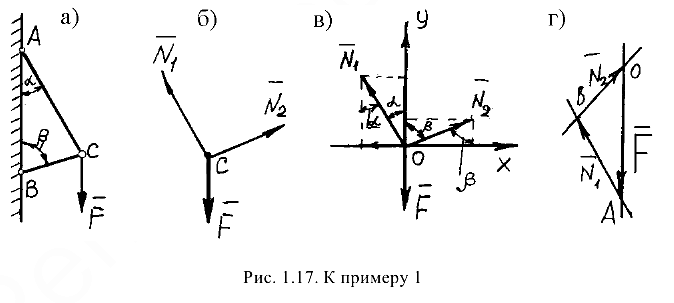
Стержни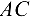 
и 
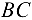(рис. 1.17, а) соединены между собой шарниром 
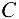, а с вертикальной стеной — посредством шарниров 
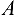и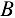 
. В шарнире 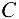приложена сила 
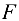=1260 Н. Требуется определить реакци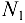и 
и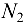 
стержней, действующие на шарнир 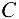, если 
.
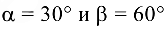Решение:
Рассматриваем равновесие точки 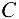, которая считается несвободной, так как на нее наложены связи в виде стержне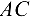й и 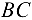. Освобождаем точку 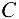от связей и заменяем их силами реакций связей, считая, что стержень 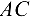растягивается, а стержень 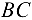сжимается под действием силы 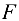. Обозначим реакцию стержня АС через 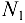, а реакцию стержня 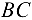через 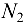. В итоге точка 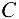становится свободной, находясь под действием плоской системы трех сходящихся сил: активной силы 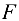и сил реакци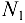й и 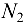(рис. 1.17,6). Приняв точку 
за начало координат, перенесем силы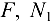 
и 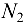параллельно самим себе в эту точку (рис. 1.17, в) и составляем уравнения проекций сил на оси координат:
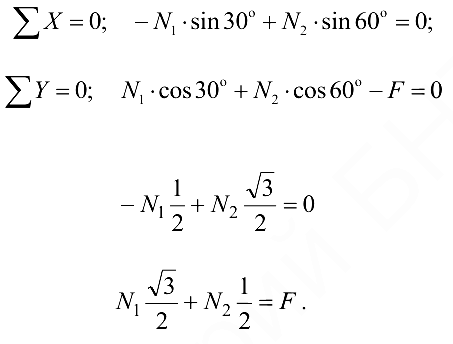
Умножим уравнение (1.2) па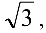 
получим
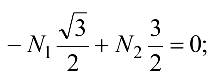
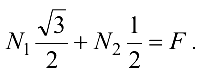
После сложения уравнений (1.3) и (1.4) получим
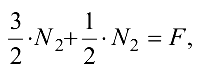
откуда
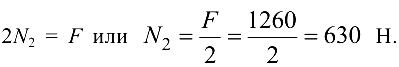
Из уравнения (1.2) получаем,что
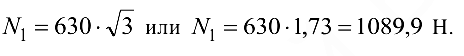
Графический метод. Для решения задачи этим методом выбираем масштаб силы 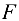(например, 10 Н = 1 мм) и строим замкнутый треугольник сил (рис. 1.17, г). Из произвольной точки 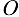проводим прямую, параллельную вектору 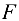, и откладываем на этой прямой в выбранном масштабе вектор 
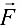. Из конца вектора 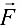(точка 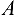) проводим прямую, параллельную вектору 
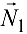, а из точки 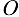— прямую, параллельную вектору 
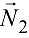. Пересечение этих прямых дает точку 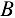. Получили замкнутый треугольник сил 
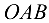, стороны которого в выбранном масштабе изображают силы, сходящиеся в точке 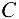. Величины сил 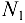и 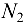определим после измерения сторон 
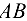и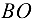 
треугольника .
Ответ:
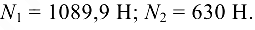
Эта задача с решением взята со страницы решения задач по предмету «прикладная механика»:
Решение задач по прикладной механике
Возможно эти страницы вам будут полезны:
