Курсовая работа К4
Стержень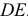 
, составляющий угол 
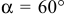с вертикалью, вращается вокруг оси 
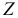с угловой скоростью 
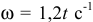. По стержню перемещается кольцо 
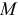по закону 
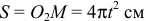(прил. 7, рис. КЗа ).
Определить абсолютную скорость и абсолютное ускорение кольца 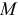в момент времени 
.
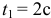Решение
Будем считать, что в заданный момент времени стержень 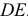находится в плоскости чертежа. Выбираем две системы координат. Неподвижную 
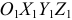, связанную с неподвижным подпятником 
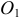и подвижную, связанную со стержнем .
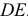У подвижной системы показываем одну ось, направленную вдоль стержня.
Согласно определениям движение кольца вдоль стержня 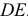считается относительным движением, а вращение кольца вместе со стержнем относительно оси 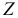— переносным движением.
- Определяем положение точки в момент времени .
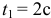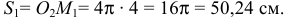
- Определяем абсолютную скорость точки
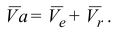
При определении относительной скорости переносное движение мысленно останавливаем. Считаем, что кольцо движется только по стержню
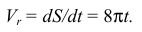
При
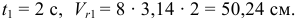
Вектор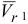 
направлен в сторону возрастания 
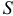. Определяя скорость точки в переносном движении, мысленно останавливаем относительное движение. Считаем, что кольцо совершает вращательное движение вместе со стержнем 
.
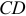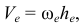
где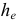 
— расстояние от точки (кольца) 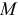до оси вращения.
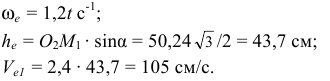
Вектор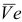 
направлен перпендикулярно плоскости чертежа от нас. На рис. КЗа прил. 7 этот вектор показываем параллельным оси 
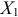, направляя его в сторону, противоположную оси .
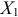Угол между векторами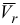 
и 
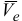равен 90°, поэтому модуль абсолютной скорости будет равен
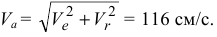
- Определяем абсолютное ускорение точки.
Абсолютное ускорение точки равно геометрической сумме относительного, переносного и кориолисова ускорений
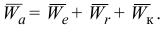
Относительное ускорение найдем по формуле
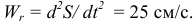
Вектор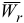 
направляем в сторону вектора 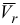, т. к. знаки относительной скорости 
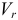и ускорения 
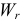одинаковы.
Переносное движение точки (кольца) — вращательное, поэтому переносное ускорение определяем как геометрическую сумму нормального и касательного ускорений
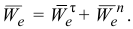
Модули нормального и касательного ускорений в переносном движении найдем по формулам
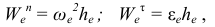
где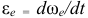 
— модуль углового ускорения стержня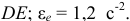 
При
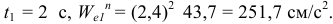
Вектор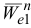 
направляем от точки 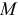к оси вращения 
.
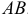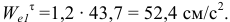
Вектор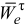 
направляем по касательной к траектории переносного движения в ту же сторону, что и вектор 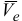, т. к. знак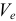и 
и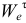 
одинаковые.
Определяем ускорение Кориолиса
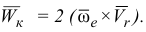
Вектор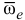 
, направлен вдоль оси переносного вращения 
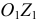в ту сторону, откуда вращение тела видно происходящим против хода часовой стрелки. Стержень 
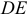поворачивается в сторону увеличения угла 
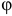, поэтому вектор 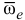, направляем вверх.
Модуль ускорения Кориолиса
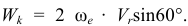
При
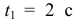
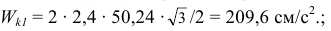
Направление вектора ускорения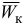 
определим согласно правилу векторного произведения или по правилу Н. Е. Жуковского.
Вектор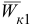 
направлен параллельно оси 
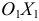противоположно направлению этой оси. Абсолютное ускорение определяется аналитически, проектируя векторное равенство (2.13) на оси системы координат 
.
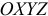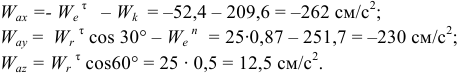
По проекциям определяем
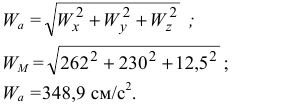
Ответ:
