Оглавление:
Задача №1.1.12.
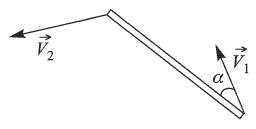
Стержень длиной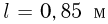 
движется в горизонтальной плоскости. В некоторый момент времени скорости концов стержня равны 
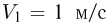и 
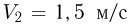, причем скорость первого из них направлена под углом 
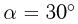к стержню. Какова угловая скорость 
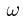вращения стержня вокруг его центра?
Решение:
Поскольку скорости концов стержня в неподвижной системе отсчета различны, он совершает относительно этой системы сложное движение, представляющее собой сумму поступательного и вращательного движений. При этом скорости разных точек стержня различны. Для определения угловой скорости вращения стержня удобно перейти в систему отсчета, поступательно движущуюся вместе с его центром. С этой целью нужно вначале определить скорость центра стержня относительно неподвижной системы отсчета.
Из геометрических соображений ясно, что в данной системе радиус-вектор центра стержня равен полусумме радиус-векторов его
концов: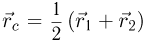 
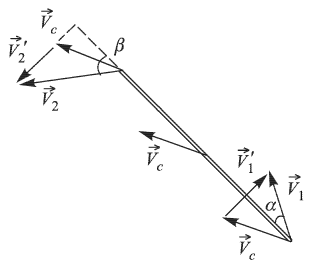
. Дифференцирование этого равенства по времени дает нам аналогичное соотношения для скорости центра стержня: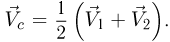 
Согласно закону сложения скоростей скорости концов стержня в системе отсчета, связанной с его центром, выражаются следующим образом (см. рисунок):
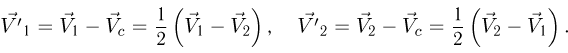
Из постоянства длины стержня вытекает, что проекции скоростей его концов на направление стержня в каждый момент времени совпадают:
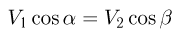
Поэтому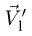 
и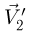 
перпендикулярны стержню, причем 
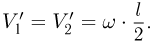Следовательно,
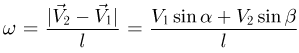
Учитывая, что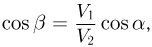 
получаем ответ:
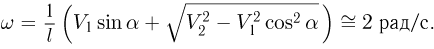
Эти задачи взяты со страницы решения задач по физической механике:
Решение задач по физической механике
Возможно эти задачи вам будут полезны:
