Оглавление:
Степенные ряды
Степенным рядом называется ряд вида
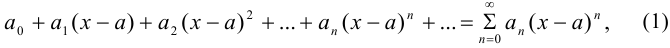
где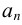 
— числа, называемые коэффициентами степенного ряда.
При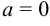 
степенной ряд имеет вид
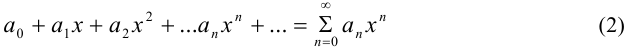
Этот ряд всегда сходится при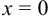 
.
Теорема Абеля. Если степенной ряд сходится при некотором значении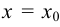 
, отличном от нуля, то он сходится и притом абсолютно, при всех значениях 
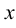, для которых 
.
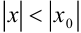Следствие. Если степенной ряд расходится при некотором значении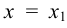 
, то он расходится и при всех значениях 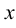, для которых 
.
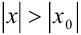Интервал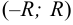 
называется интервалом сходимости указанного ряда. На концах интервала сходимости ряд может сходиться или расходиться. Если степенной ряд сходится на всей числовой оси, то полагают 
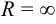; если он сходится только при 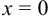, полагают 
.
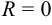Радиусом сходимости степенного ряда (2) называется такое число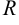 
, что при 
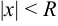ряд сходится, а при 
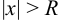— расходится.
Радиус сходимости вычисляется по одной из формул:
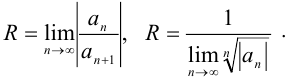
Задача №114.
Определить радиус сходимости степенного ряда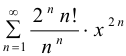 
.
Решение:
Имеем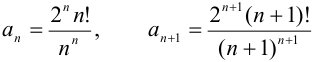 
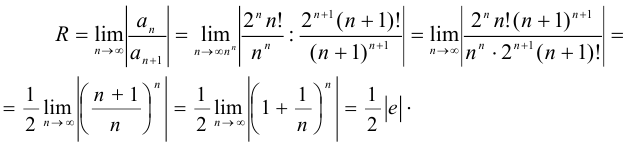
Следовательно,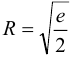 
.
Задача №115.
Найти область сходимости ряда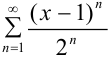 
.
Решение:
Этот ряд является степенным рядом вида (1). Сделаем замену: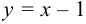 
и сведём его к ряду (2). Найдём радиус сходимости для ряда 
.
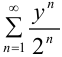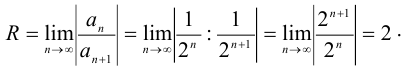
Интервал сходимости ряда — (-2; 2). Исследуем поведение ряда 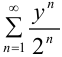на концах интервала сходимости. При 
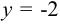получаем знакочередующийся числовой ряд 
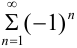, который расходится.
При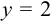 
числовой ряд 
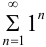тоже расходится, так как не выполняется необходимое условие сходимости рядов. Таким образом, областью сходимости ряда 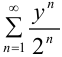является промежуток (-2; 2).
Так как 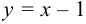, то имеем —
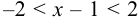или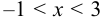 
, т. е. область сходимости данного ряда (-1; 3).
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
