Степени с натуральными и целыми показателями и их свойства
Выше, в пункте 1.1 данного раздела, уже было введено понятие натуральной степени натурального числа. Расширим это понятие и сформулируем определения степеней с натуральным и целым показателями для действительных чисел.
Введём вначале понятие натуральной степени n для произвольного действительного числа а . Если действительное число а умножить само на себя п раз 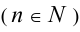 , то это произведение
, то это произведение 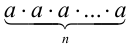 называют n -й степенью числа а и обозначают
называют n -й степенью числа а и обозначают 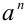 ,т.е.
,т.е.
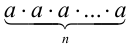
При этом число а называется основанием степени, а n — показателем степени. При n = 1 для любого действительного а имеем 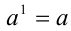 . Нулевая степень вводится только для действительных чисел, отличных от нуля, при этом для
. Нулевая степень вводится только для действительных чисел, отличных от нуля, при этом для 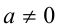 полагают
полагают 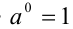 . Число 0° не определено, это запрещённая операция.
. Число 0° не определено, это запрещённая операция.
Определим теперь степень с целым отрицательным показателем. Она, как и нулевая степень, вводится только для действительных чисел, не равных нулю. Пусть n — произвольное натуральное число. Степенью действительного числа 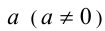 с целым отрицатель-ным показателем
с целым отрицатель-ным показателем 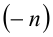 называют число, обратное степени с натуральным показателем n :
называют число, обратное степени с натуральным показателем n :
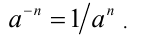
Целая отрицательная степень числа нуль, т.е. 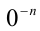 , не определена.
, не определена.
Рассмотрим теперь основные свойства степеней с целыми показателями, опираясь непосредственно на определения степени числа и свойства арифметических операций над действительными числами.
Теорема (свойства степеней с целыми показателями). Для любых двух действительных и отличных от нуля чисел а ,b и произвольных целых чисел n , m верны равенства:
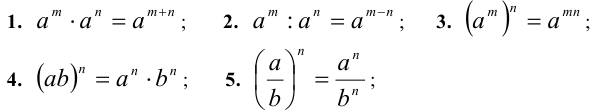
Пусть 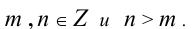
Тогда 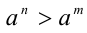 , если
, если 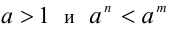 , если
, если 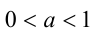
Доказательство приведём для случая натуральных показателей m и n

При доказательстве последнего свойства мы воспользовались свойством 8 числовых неравенств: 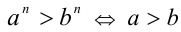 (см. пункт 2.1 раздела 2), из которого вытекает, что при
(см. пункт 2.1 раздела 2), из которого вытекает, что при 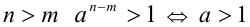 . Аналогично, если
. Аналогично, если 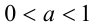 , то
, то 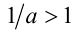 и тогда при
и тогда при 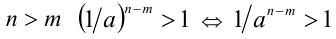 и, следовательно, по свойству 7б числовых неравенств
и, следовательно, по свойству 7б числовых неравенств 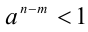
Замечание. Если среди чисел n и m есть равные нулю или отрицательные, то в приведённых выше равенствах (и неравенствах) следует заменить соответствующие множители согласно определению нулевой и целой отрицательной степени. Например, свойство 4 при n< 0 доказывается так:
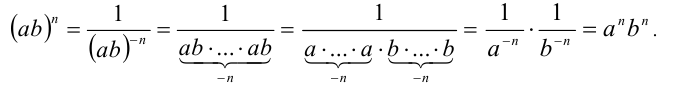
Подробнее с доказательствами свойств степеней для случая нулевых и целых отрицательных показателей можно ознакомиться, например, в книге.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

