Оглавление:
Степени с иррациональными показателями
Определим, наконец, понятие степени с иррациональным показателем для положительных действительных чисел.
Начнём с определения положительной иррациональной степени положительного числа. Рассмотрим действительное число а > 1 и положительное иррациональное число x. Под иррациональной степенью x числа а понимается такое действительное число 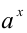 , которое удовлетворяет неравенству
, которое удовлетворяет неравенству
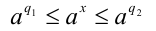
сразу для всех рациональных чисел 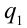 и
и 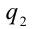 таких, что
таких, что 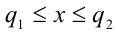 . Без доказательства принимается, что такое число существует и притом только одно.
. Без доказательства принимается, что такое число существует и притом только одно.
Пусть теперь даны число а такое, что 0 < а < 1, и положительное иррациональное число x. Под иррациональной степенью x числа а будем понимать такое действительное число 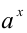 , которое удовлетворяет неравенству
, которое удовлетворяет неравенству
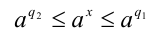
сразу для всех рациональных чисел 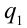 и
и 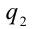 , таких, что
, таких, что 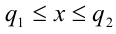 . Без доказательства принимается, что такое число также существует и единственно.
. Без доказательства принимается, что такое число также существует и единственно.
Если основание степени а = 1, то считают, что 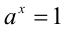 для любого действительного (в том числе иррационального) числа x .
для любого действительного (в том числе иррационального) числа x .
Если а = 0, то для любого положительного действительного x полагают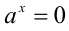 . При x < 0 число
. При x < 0 число 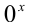 не определено.
не определено.
Введём понятие отрицательной иррациональной степени. Она определяется только для положительного основания. Пусть теперь даны положительное число а и положительное иррациональное число x. Под числом 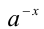 будем понимать число, обратное к
будем понимать число, обратное к 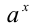 , т.е.
, т.е. 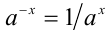 .
.
Такое число существует и единственно (без доказательства).
Замечание. В силу вышеприведённых определений любая действительная степень x положительного числа а всегда положительна, т.е.
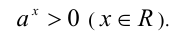
Отметим также тот факт, что степени с иррациональными (действительными) показателями удовлетворяют свойствам, аналогичным свойствам степеней с рациональными показателями.
На вступительных экзаменах задачи, при решении которых существенно используются свойства арифметических корней и степеней, встречаются достаточно часто. Поэтому важно не только знать эти свойства, но и уметь быстро и правильно оперировать ими при упрощении разного рода выражений, встречающихся в задачах.
Пример №115.
Решить уравнение 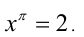
Решение:
На ОДЗ 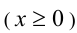 уравнение имеет единственный корень
уравнение имеет единственный корень 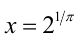 .
.
Пример №116.
Доказать неравенство
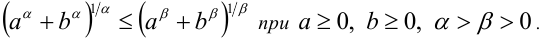
Доказательство. Если а = 0 или b = 0, то утверждение очевидно. Пусть а > 0 и b > 0. Возможны два случая.
1) Пусть 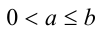 . Тогда
. Тогда 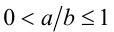 и так как
и так как 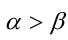 , то
, то 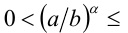
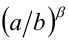 . Значит,
. Значит, 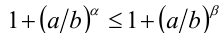 , и, следовательно,
, и, следовательно,
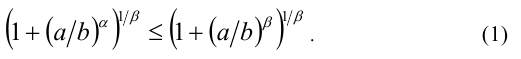
Далее, так как 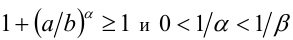 , то имеем
, то имеем
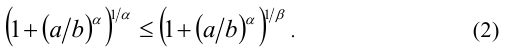
Из неравенств (1), (2) и свойства транзитивности следует, что
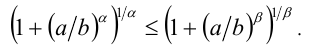
Отсюда, преобразуя, получаем:
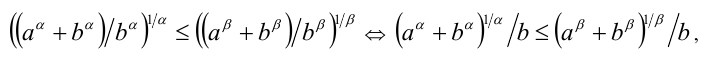
и так как b > 0 , то требуемое неравенство доказано.
2) В случае 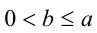 доказательство проводится аналогично.
доказательство проводится аналогично.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

