Оглавление:
Степень с рациональным и действительным показателем
а) Степень с рациональным показателем определяется равенством
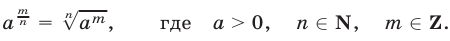
б) Свойства степени с рациональным показателем (р, q — рациональные числа, а > 0, b > 0).
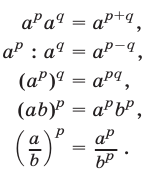
в) Степень с действительным иррациональным показателем х и основанием а, где а > 0, определяется как действительное число (обозначается 
), являющееся пределом последовательности 
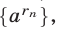где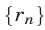 
— последовательность рациональных чисел такая, что 
При этом для степени с любым действительным показателем справедливы те же свойства, которыми обладает степень с рациональным показателем. Это доказывается в курсе высшей математики.
Пример №19.
Освободиться от иррациональности в знаменателе дроби
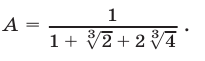
Решение:
Обозначим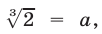 
тогда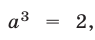 
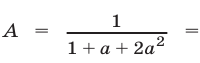
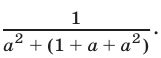Умножая числитель и знаменатель полученной дроби на 
и применяя формулу разности кубов, запишем А в следующем виде:
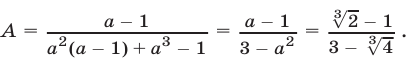
Снова применяя формулу разности кубов, получаем
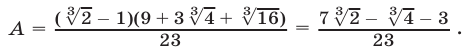
Ответ: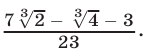 
Пример №20.
Доказать, что
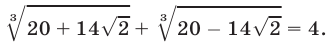
Доказательство. Пусть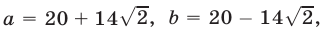 
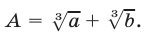Применяя формулу куба суммы и учитывая, что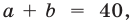 
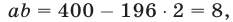получаем
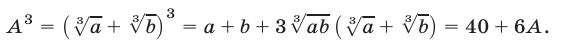
Таким образом, левая часть А рассматриваемого равенства является корнем уравнения
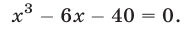
Это уравнение имеет корень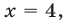 
а его левую часть можно записать в виде 
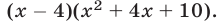Так как уравнение 
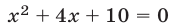не имеет действительных корней, а левая часть равенства А — действительное число, то
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
| Производные пропорции примеры с решением |
| Действия с корнями (радикалами) примеры с решением |
| Логарифмы примеры с решением |
| Числовая последовательность и арифметическая прогрессия с примерами решения |
