Степень с любым вещественным показателем

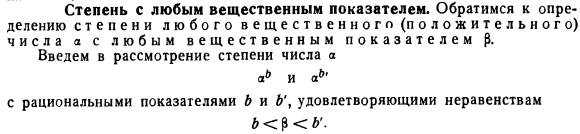
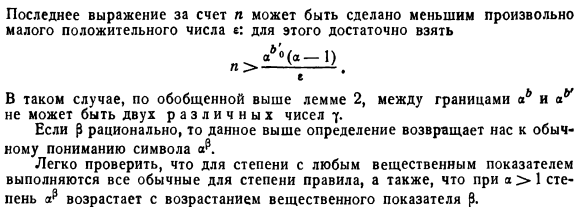
Степень с любым вещественным показателем

Степень с любым вещественным показателем. Возвращает к определению порядка вещественного (положительного) a с произвольным вещественным показателем P. Мы введем степень ай да ай ’ Рациональные показатели B и \B удовлетворяют неравенству Б $ б’. Порядок числа (a> 1*) с показателем степени p называется вещественным числом (обозначается знаком aP), которое содержится между порядком ab и ab>. а * 7 А6′. (1） In дело в том, что множество степеней{ab}есть, например, любая степень a и. Затем[6]] 7 = $ Ир {АБ}. б $ Об этом номере.

Нетрудно заметить, что такое число всегда существует. Людмила Фирмаль

• В Фактически, учитывая возможность увеличения b и уменьшения b \так, чтобы построенное число 7 удовлетворяло условию (1), здесь нет необходимости в знаке равенства. Далее обратимся к доказательству единственности числа, определяемого этими условиями. Для этого, прежде всего, обратите внимание, что даже если вы опустите требование о том, что числа 5, 5′ и e обязательно разумны, Лемма 2 n * 3 останется действительной. Доказательства остаются прежними. Затем установите 1 очень простое, но полезное неравенство. если n-положительное целое число, большее 1 и 7> 1、 7e> 1-й(T-1). (2).

• Фактически, множество 7 = 14-X(если X> 0, то по биномиальному выражению Ньютона） (1 + х)* = 1 + пх + …; Потому что неписаный термин положительный、 (1 + х) » > 1 + пх、 Это эквивалентно неравенству(2). Если вы установите 7 = an (in> 1) в этом неравенстве, вы получите неравенство Один (3） Использовать это. (N * 4, Примечания) потому что мы знаем, что вы можете выбрать числа b и b ’、 н Разница b ’ b была невелика-естественная данность г-АВ = * б(аб, б -) СА(АУ-1） ;「 а-1П Г-н L; затем, по неравенству (3)、 Наконец, если вы укажете любое из чисел b в b ’ 9、\ * ).

Этот случай может быть ограничен: например, если последнее выражение по n может быть меньше любого небольшого положительного числа c. Людмила Фирмаль

• Для этого вам нужно、 В этом случае, по обобщенной выше Лемме 2, не может быть 2 разных чисел 7 между границей a *и ay. если p-рациональное число, то приведенное выше определение возвращает к обычному пониманию символа A. Для ордеров с действительными экспонентами легко видеть, что ордер удовлетворяет всем обычным правилам, и что ордер увеличивается с увеличением действительного экспонента, 0, в случае a> 1.

Смотрите также:

Решение задач по математическому анализу

Определение и свойства произведения вещественных чисел.	Логарифмы.
Существование корня. Степень с рациональным показателем.	Измерение отрезков.