Оглавление:
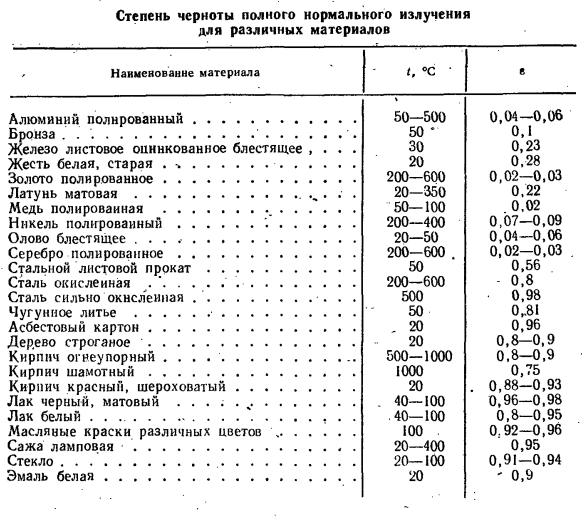


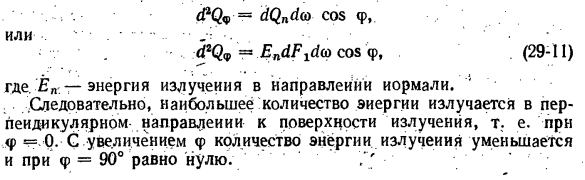



Степень черноты полного нормального излучения для различных материалов
- Чернота всех нормалей различных материалов т, ° С * Название материала Полированный алюминий … Бронза …………. , Матовая оцинкованная жесть Белая жесть, старая. ……….. Золотая полировка ……….. Мэтт Брасс …… Полированная медь ………. Полировка никеля …… , , , Олово потрясающе. , , ……….. Серебряный лак … Стальная пластина … Сталь была окислена. »……….. Сталь очень окисляется. …….. Чугун … Асбестовый картон … Строганная древесина ………
Огнеупорный кирпич. , , …….. Шамотный кирпич … Кирпичи красные и грубые … . …. …. Белый лак ……………… Масляные краски разных цветов. , Сажевая лампа … Стекло …………………. Белая эмаль …… 50-500 0,04-0,06 50 ‘0,1 30 0,23 20 0,28 200-600 0,02-0,03 20-350 0,22 50-100 0,02 200-400 0,07-0,09 20-50 0,04-0,06 От 200 до 600. От 0,02 до 0,03 50 0,56 200 ~ 600-0.8 500 • 0,98 50-031 20 0,96 20 0,8-0,9 500-1000 0,8-0,9 1000 0,75 20. 0,88-0,93 40-100 0,96-0,98 .40-100 0.8-0.95 100. 0.92-0.96 20-400 0,95 20-100 0,91-0,94 20-0.9 Выражение (29-9)
Лак черный и матовый Людмила Фирмаль
справедливо для всех тел, так как его можно использовать вместо второго тела, и является математическим представлением закона Кирхгофа. ••. «Отношение излучательной способности объекта к поглотителю одинаково для всех серых объектов при одинаковой температуре и равно излучательной способности черного тела при той же температуре. Это соотношение может быть получено термодинамически. Предположим, что в закрытой полости находятся
два объекта. Один черный, а другой серый. Согласно второму закону термодинамики, каждое тело должно выделять и поглощать одинаковое количество энергии для поддержания теплового равновесия. Невыполнение этого условия нарушило бы температурную эквивалентность между поверхностью полости и корпусом. Энергия излучения ls \ dK полностью попадает на единицу
поверхности черного тела, полностью поглощается и одновременно излучает энергию. Следовательно, единичная поверхность серого тела поглощает, поэтому l8 \ dlAs = E & dX и 1 $ \ =. Только часть энергии ls \ dk является падающей. Если поглощающая способность тела равна / 4x, тело поглощает количество энергии, равное / d ^ l ^, и
- выделяет такое же количество. Энергия излучения серого тела равна E \ dX. То есть l & AxdK — это ExdX … Подстановка значения черного тела ls \ в последнем уравнении дает закон Кирхгофа. E = Ey.dK или E $ k = E ^ / A *. Согласно закону Кирхгофа, если способность организма поглощать низка, это снова. Низкая излучательная способность (полированный металл). Полностью черный корпус с максимальной
поглощающей способностью обладает самой высокой излучательной способностью. Пребывание Кирхгофа действительно для монохроматического излучения. Отношение поглощающей способности на одной длине волны к интенсивности излучения объекта на конкретной длине волны одинаково для всех объектов, если оно численно равно интенсивности излучения абсолютно
черного объекта при той же температуре и на той же длине волны и температуре. , е. Является функцией только длины волны и температуры. Eb / Ak = / xMx = E9x = /, * = / (K T) .. (29-10) волны, может поглощать энергию на той же длине волны. Если тело не поглощает энергию в некоторой части спектра, оно не будет излучать в этой
Таким образом, объект, который излучает энергию на любой длине Людмила Фирмаль
части спектра. Из закона Кирхгофа мы видим, что степень черноты серого объекта e при той же температуре численно равна коэффициенту поглощения A. •. e = IJI $ \ = ‘E / Es = C / Ce-L.- Закон Ламберта. Высвобождаемая из тела энергия распространяется в пространстве с различной интенсивностью. Закон, устанавливающий зависимость от направления интенсивности излучения, называется
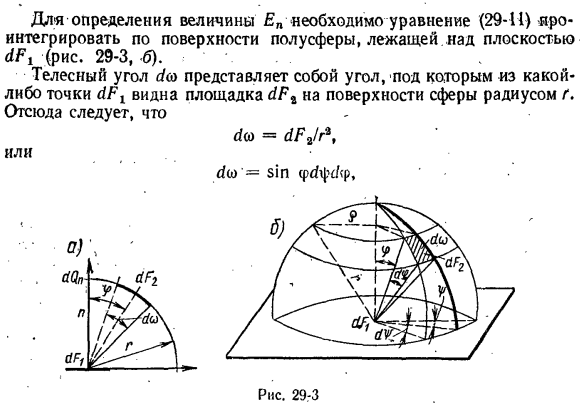
законом Ламберта. Согласно закону Ламберта количество энергии, выделяемой поверхностным элементом dFx в направлении элемента dF2, представляет собой количество энергии, излучаемой вдоль нормальной линии dQni и пространственного угла d (направление излучения от нормальной линии o И cosф) (Рис. 29-3, а): • (PQq, = dQnd (o cosф, Или — «•. …….. ••• • г. — (PQv = EndF ^ a cosφ, … (29-11) Где Ep — лучистая энергия в нормальном направлении. , , В результате
максимальное количество энергии излучается перпендикулярно поверхности излучения. Другими словами, когда угол долготы. Подставляя полученное уравнение (29-11) <PQ9 = EndF] L sinφ ^ φ ^ φ-ωBφ. Интегрируйте эту формулу по всей поверхности полушария. Другими словами, оно находится в пределах диапазона изменения угла φ от 0 до n / 2 и угла r | z от 0 до 2π. В результате интегрирования вы можете видеть, что энергия, излучаемая элементом dFlt в
полушарии, равна EdFt. так , 2l I / 2 , EdFL = EndFl ^ s’nФcosф ^ ф = иЕпс // 7! , » $ = 0Ф = 0- ■ Где * , , En = // == — C (G / 100) 4 = -C0 (G / 100) 4. Я л •• Последнее уравнение показывает, что энергия излучения в нормальном направлении в i раз меньше плотности интегрального полусферического излучения полностью черного (или серого) объекта, который определяется по закону Стефана-Больцмейера. Таким образом, закон Ламберта (29-11) принимает следующую форму: = -С0 (Г / 100) 4 dco cosf ^ / v I (29-11 ‘) • ‘• l Последнее уравнение было
получено для интегрального излучения элемента dFit, но справедливо для монохроматического излучения. Уравнение (29-11 ‘) является основой для расчета радиационного теплообмена между поверхностями конечных размеров. Закон Ламберта полностью верен для абсолютно черного или серого тела. А для объектов с рассеянным излучением только в диапазоне φ = 0-60 °. Для полированных поверхностей метод Ламбберта не применим.
Смотрите также:
Решение задач по термодинамике
| Общие сведения о тепловом излучении | Теплообмен излучением между твердыми телами |
| Основные законы теплового излучения | Экраны |

