Оглавление:



Статические моменты площади. центр тяжести площади
- Статические моменты в этом районе. Центр тяжести площадь Выделите Эле- Линия- Рассмотрим любую фигуру, связанную с координатными осями (поперечное сечение балки) Oz и Oh(рис. 9). По аналогии с выражением момента силы относительно любой оси
можно сделать выражение момента области, называемое статическим моментом. Таким образом, произведение элемента площади DF с расстоянием г от оси OZ д 2-г ДФ, ,
называют статический момент элементарной площадки относительно оси OZ. Аналогично Людмила Фирмаль
dSg= = zdF-это статический момент элемента области относительно оси op-amp. Суммируя такие произведения по всей площади рисунка, получаем пространственно статический момент для осей g и y: Sz=Jydf -, s v=jzd F. Статические моменты измеряются в единицах
длины(например, см3). (2.1) Куб 13º zc, yc-координаты центра тяжести (c. t.) рис. Продолжая аналогию с моментом силы, основываясь на полученной теореме о моменте, S2=Ftjc, Sv-Fz»(2.2), где F-площадь фигуры. Таким образом, координаты центроида (2.3) Прокладка умственная пусковая площадка Сы СЗ—Р>США п * Выражение Ids (2.2) это привело бы к нулю статических моментов площади относительно центральной оси (оси, проходящей через центроид). В качестве
- примера для расчета статических моментов т р е й Г О Л Ь Н И К а(рис. 10) относительно оси, проходящей через основание. 11а расстояние от нее прокрутите до Эле-в виде полосы, параллельной оси 2. Область ДФ-Б (г)ды. И я думаю, что Иметь с=Дж ГДФ Ф — По ) , О чем/? Я Хм. Еще проще решить эту проблему с помощью»выражения» (2.2). Это понятно. Ф= — FW и я; МК=± — х, з И
так оно и есть., С2-2bh * ч-ч-б • Чтобы вычислить статический момент сложной фигуры, разделите ее на простые части(рис. 11), известный соответственно как F£и Z£и y позиция. Статический момент площади всей фигуры для данной оси определяется как сумма статических моментов каждой части: S2=^i!/я+P2U2+•• * +F_-\F_£г£\ 1=1 С
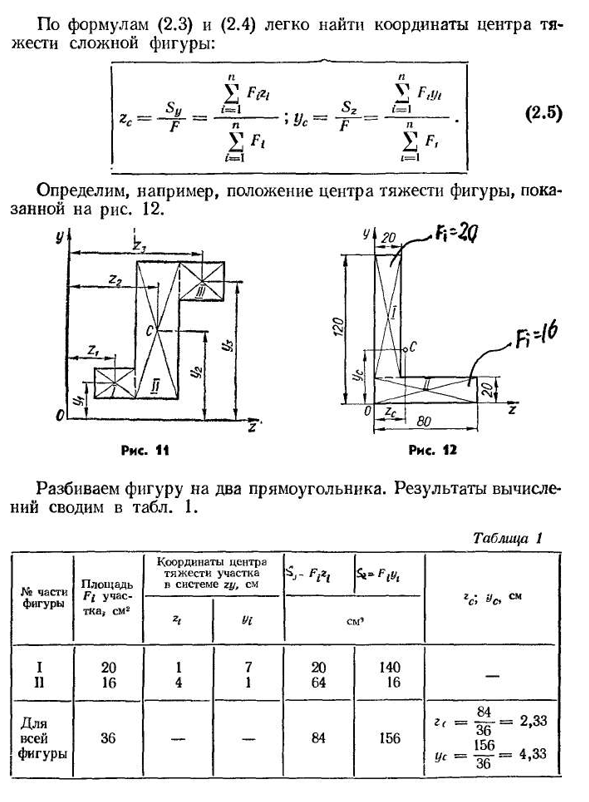
ы=+^2+ «’ +п^п=и Ф^я. • З=Л В соответствии с уравнениями 14 (2.3) и (2.4) легко Людмила Фирмаль
найти координаты центроида сложной фигуры: п п е£е е в U_f==1 * р-СЗ-ф=л-р * США — Р S F’ (’»=1 1=1 Например, определите положение центра тяжести фигуры, показанной на рисунке. 12. Разделите фигуру на два прямоугольника. Результаты расчетов сведены в таблицу. 1.
Смотрите также:
| Виды деформаций стержня. понятие о деформированном состоянии материала | Моменты инерции плоских фигур |
| Основные гипотезы науки о сопротивлении материалов | Моменты инерции сложных сечений |

