Оглавление:

Статические моменты. определение положения центра тяжести плоской фигуры
- Статический момент Центральное решение Вес плоской фигуры выражение (13-1) Называется моментом статической площади вокруг оси y и оси z (рисунок 13.1) и измеряется в см3. Если положение
центра тяжести сечения определяется как (ус \ zc), статический момент рассчитывается по следующей формуле: ■ \ / = Ezc! Sz = Fyc, где F — площадь поперечного сечения. Для сложных форм поперечного сечения: Sy- $ r = ftUi ‘(13.1a) 1 = 1 i = l Статический момент вокруг
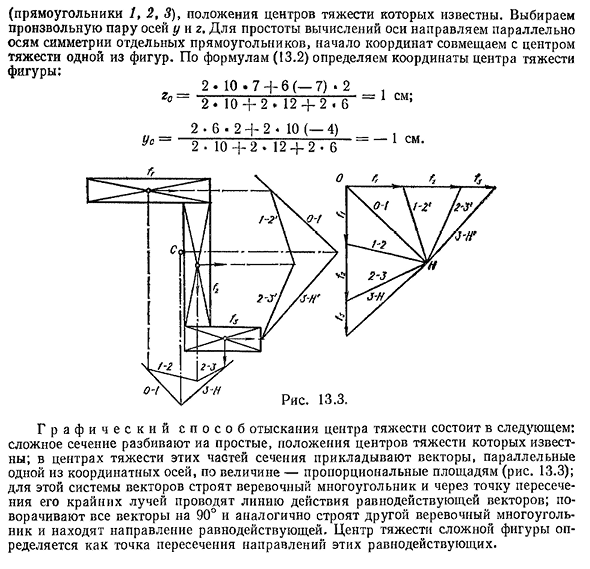
оси, проходящей через центр тяжести (ось центра), равен нулю. Рисунок Людмила Фирмаль
13.1 S = 0; Sz <= 0. Определены координаты центра тяжести фигуры относительно выбранной оси. 1 = 1 — ‘ Давай я = я N Y и г (13.2) W ft — площадь i-й части фигуры (i = 1, 2, 3 …….. n). yi и zs — координаты центра тяжести. Пример. Определите положение центра тяжести вида в плане, показанного на рисунке 13.2 (размеры даны в см).
Решения. Разделите сложные формы на простые формы. * Интеграция охватывает всю область. 248 (прямоугольник 1, 2, 3), положение его центра тяжести известно. Выберите любую пару осей y и r. Чтобы упростить вычисления, оси отправляются параллельно осям
- симметрии отдельных прямоугольников, а начало координат объединяется с центром тяжести одной из фигур. Используйте уравнение (13.2), чтобы определить координаты центра тяжести
диаграммы. 2 • 1 0,7 + 6 (-7) • 2 г ° ~ 2 * 10 + 2,1,2 + 2-6,6-1 см; 2,6 • 2 + 2. 10 (-4), C ~ 2 ■ 10 + 2. 12 + 2 • 6 _ 1 см ’ Чтобы найти центр тяжести: Сложные разделы делятся на простые разделы с известными местоположениями центроидов. Вектор, пропорциональный площади и параллельный одной из осей координат, применяется к центру тяжести этих секций сечения (рис. 13.3).
Для этой векторной системы строится многоугольный канат, и результирующая Людмила Фирмаль
векторная линия действия рисуется через пересечение его крайних лучей. Поверните все векторы на 90 °, создайте еще один многоугольник веревки и найдите направление результата. Центроид сложной формы определяется как пересечение этих результирующих направлений.
Смотрите также:
| Теории ползучести | Расчет гибких нитей |
| Расчеты с учетом ползучести | Формула Эйлера для определения критической силы сжатого стержня |

