Статически определенные и статически неопределенные задачи
Установленные для различных случаев расположения сил уравнения равновесия позволяют составить для каждого случая только определенное число независимых уравнений, налагающих соответствующие условия на систему находящихся в равновесии сил.
Задачи, в которых число неизвестных не превышает числа независимых уравнений равновесия, даваемых статикой твердого тела для данного случая расположения сил, называются статически определенными задачами, в противном случае задачи называются статически неопределенными.
Так, задача 15 была бы статически неопределенной, если бы в ней отсутствовал шарнир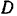 
и балка была бы неразрезной. Неизвестными в этой задаче являются модули реакций трех опор, для приложенной же к балке плоской системы параллельных сил можно составить только два независимых уравнения равновесия. Мы можем, конечно, проектируя приложенные к балке силы на оси различного направления и составляя уравнения моментов относительно различных центров, написать сколько угодно уравнений, но независимыми из них будут только два.
Статически неопределенной будет и задача о равновесии груза, подвешенного на трех нитях, расположенных в одной плоскости (рис. 67). Неизвестных по модулю сил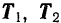 
и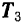 
мы будем здесь иметь три, тогда как независимых уравнений для плоской системы сходящихся сил можно составить только два.
Причина недостаточности одних уравнений статики для решения статически неопределенных задач заключается в том, что в теоретической механике мы рассматриваем все тела как абсолютно твердые, не деформирующиеся под влиянием приложенных к ним сил.
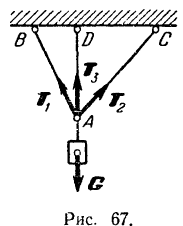
Если нити в последнем примере нерастяжимы, то любую из трех нитей можно отбросить, не нарушая равновесия точки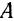 
и подвешенного к ней груза 
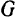и не изменяя положения двух других нитей. С точки зрения статики абсолютно твердого тела, одна из трех данных нитей, а следовательно, и одна из неизвестных сил является лишней. В случае же реальных нитей под действием веса груза точка 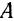его подвеса несколько опустится (иначе, чем при наличии только двух нитей) и каждая из трех нитей получит соответствующее удлинение.
Для решения данной задачи, как и вообще всех статически неопределенных задач, нужно принять во внимание деформации, испытываемые в действительности всеми телами под действием приложенных к ним сил. Учтя эти деформации, всегда можно написать столько дополнительных уравнений, сколько нужно для того, чтобы общее число уравнений, вместе с уравнениями статики, равнялось числу неизвестных в данной задаче.
Изучение зависимости между деформациями тел и действующими на них силами является предметом науки о сопротивлении материалов, строящейся на базе теоретической механики и являющейся одним из разделов механики изменяемого твердого тела. В этой науке рассматриваются и методы решения статически неопределенных задач.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
