Оглавление:





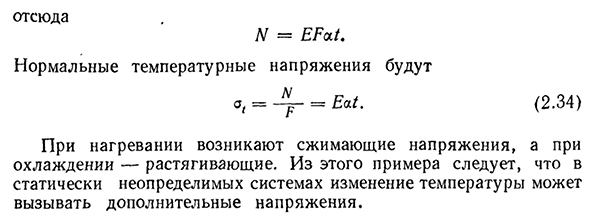

Статически неопределимые задачи при растяжении и сжатии
- Статически необнаружимые задачи Под напряжением и сжатием Статическая неопределенность — это проблема, которая не может быть решена с использованием только статических уравнений (уравнений равновесия). Уравнение дефекта состоит из условий деформации. Давайте следовать порядку решения этих проблем на примере. P R I m e R1. Найти напряжение в призменном стержне, запечатанном с двух концов, от одной внешней продольной силы P (рис. 66, а). Откажитесь
от одного из уплотнений и замените его действие неизвестной силой реакции X (Рис. 66,6). В этом случае вы можете составить одно уравнение равновесия: = 0; A-P + X = 0; A + X = R (a) Это уравнение имеет неизвестные силы A и X, которые не найдены в том же уравнении. Следовательно, проблема не является статически определенной. Для этого решения вам нужно создать дополнительные уравнения деформации.
Общая длина стержня не изменяется, поэтому D / = 0. (б) может быть выражена двумя Людмила Фирмаль
способами как сумма удлинения от общего удлинения D / сила P и сила X: D / = РА EF XI EF = 0 Или как сумма двух разделов А и Б разложения » Kt У I a i (P-X) a X L Д / Д / Д Д / У ПП-0. Три * Легко видеть, что оба метода приводят к одному и тому же результату: Из статического уравнения (а) мы находим реакцию у левого уплотнения: A = P- ± -. Схема внутренних сил показана на рисунке. 66, V. Самые большие напряжения: _ ^ t h____R B тах R R R * я P R I m e R s
клеммное напряжение в 2. Сила Р измеряется цилиндрической медью со стальным сердечником (рис. 67). Определите медные и стальные части стержня. Рисунок 67а Из равновесия NM + MS = P, (b) где / Um — сила, приложенная к медному каркасу, а Nc — сила, приложенная к стальному центру. Чтобы установить, как сила P распределяется между стальными и медными деталями, создайте уравнение деформации D / s == D / m, которое представляет равенство деформации стальных и медных частей. Замена значений D / s и D / m на значения в соответствии с законом Гука, N Cl_ECFC ~ EMFM • И ‘ Но с тех пор ЕС и Это Следовательно, отношение напряжений в
- стальной и медной частях стержня равно отношению модулей упругости этих материалов. Решите уравнения (b) и (d) вместе, чтобы получить желаемое напряжение P £ m разрешение ° m_EmFm + EcFc «° C» Em £ m + ^ s * Тогда попробуйте EU = 2EM-, FM = 2FC a = -R E «= -L и o — R 2 £ m_ •» £ m2 £ s2 £ s4 £ s I ° C ~ EM2ES4-2 £ s ~ 2 £ s ‘ Если вы теперь утроите площадь меди, FM = 6FC Broadcast = = 2 л. * EUSFC + ZEUFC8Fc * но P2E * _L 4-2 с использованием EM6 4ES с использованием 4ES Следовательно, увеличение площади поперечного сечения любого элемента статической неопределенной системы не будет уменьшать напряжение этого элемента снова и снова, а во всех элементах системы. P R и я R3. Бесконечно твердый стержень подвешен на трех стальных стержнях. Определите силу в стержне
от силы Р, приложенной к центру балки (рис. 68, а). 、 、) ツ ツ ツ ツ ツ ツ ツ ツ 、 、 、 、 、 、 、 、 、 、 、 、 68, b) Заменить на нижнюю часть действия стержней N, N2 и N3. Для этой задачи можно составить два уравнения равновесия: X = 0; N t + N2 + XS-P = 0; X1H-x2 | / -Lgz = P;. (D) 68 ^ M и = 0; PLN ^ -N ^ O-, N ^ + N t L ^ P — ^ -. (E) Три неизвестных силы Nt, N2 и ^ z получаются из двух полученных уравнений. Проблема не может быть определена, проблема является статически неопределенной. Давайте составим уравнение деформации. Для риса. 68 и пунктирная линия указывают положение стержня после деформации стержня. Из сходства треугольника ib2 и AiCiC2 это выглядит так D / 2-D / j = D / 3-D / i. Подстановка значения преобразования здесь дает следующее Я один Ll
Решение уравнений (d), (e) и (g) вместе найдет все неизвестные силы в стержне. P R и я R4. Бесконечно жесткий стержень должен быть закреплен на одном Людмила Фирмаль
конце и подвешен на двух стержнях (подвешенных к потолку на рис. 69, а). При сборке системы необходимо тянуть солнечный стержень, что вызывает сжатие стержня. Определите силу, создаваемую на стержневой паре и DE. Эта система является статически неопределенной, потому что есть только три статических уравнения для определения четырех ответов. Деформация системы обозначена пунктирной линией на рисунке. 69, а. Заменить действие стержня на балку в результате их усилий (рис. 69, б). Давайте создадим статическое уравнение: 2 ^ = 0; СП, £, — = 0. (Вт) 70 Использование двух более сбалансированных уравнений 2X = 0 и 2Y == 0 включает в себя две поддерживающие реакции, которые нам не интересны на шарнире A, Получено из условий деформации D / g-A / j =
Sentner • Подставляя значение преобразования EFi (А) Совместное решение статического уравнения (z) и уравнения деформации (I) позволяет легко найти силу в стержне: 4f, F, £ l2F- | -l1F2L? L] L2F} F2E Из этого примера видно, что неточности при изготовлении определенных элементов статически неопределенной системы будут прилагать усилия к другим элементам системы. По равномерному нагреву всего стержня при P R и me R 5. T ° определяется напряжение призматической балки, герметизированной на двух концах (рис. 70, а). Когда температура повышается, планка имеет тенденцию продлевать и расширять давление уплотнения, где происходит реакция. Отбросим одну из модификаций (рис. 70, б). После этого
стержень можно свободно удлинить на величину A / z = горит. Под действием внутренней силы N, равной отклику опоры, стержень должен уменьшиться на ту же величину. или N1 EF 71 где N = EFat. Напряжение нормальной температуры Ешь. (2.34) Сжимающее напряжение возникает при нагревании, а растягивающее напряжение возникает при охлаждении. Из этого примера в системах, которые не могут быть обнаружены статически, изменения температуры могут вызвать дополнительное напряжение.
Смотрите также:

