Оглавление:



Статически неопределимые системы при растяжении и сжатии
- Статически неопределимой системы Под напряжением и сжатием Системы, которые не могут быть вычислены только уравнениями равновесия, называются статически неопределенными. Недостающее уравнение состоит из условий совместимости деформаций. Количество дополнительных уравнений характеризует степень
статической неопределенности системы. Особенности статической неопределенной системы: распределение внутренних сил в статической неопределенной системе зависит от коэффициента жесткости элемента- Рис 2.6. По мере увеличения жесткости этого элемента сила этого элемента увеличивается или уменьшается в остальном; в статически неопределенных системах-
неточность изготовления отдельных элементов, отсутствие опорных креплений Людмила Фирмаль
и т. д. Например. Определите силу в статической неопределенной системе стержня, как показано на рисунке. 2.6, а, представляет собой бесконечно жесткий стержень, подвешенный на трех стержнях. Крайние стальные элементы с одинаковой площадью, средние-медные, их площадь поперечного сечения F2=3F\; P=100kN; модуль упругости EC=2 * 105mpa; m=1105mpa;1G=0,8 м;12=1,5 м;13=1,0 м; a=1,0 м; b= = 0,5 м; C=0,8 м. Решение. С помощью метода seciii
составляются условия равновесия: SK=Mi+^ + Ms-P=0 Или L\ag8 4-M3=100kN; (a) 2l4l=N2 (a+b)-RA+N3 (a+b+C)=0 или 1, 5M2-B2, ZL^z=100kN. (4>)из двух уравнений равновесия невозможно определить внутренние силы трех неизвестных величин: N±, N2 и N3. Мы используем геометрическую структуру схемы деформации, чтобы составить недостающее уравнение(рис. 2.6, Б): А/Д-Л?3__л/—д/3а-б-ф-с 24 это уравнение совместимости деформаций. Учитывая законы этого
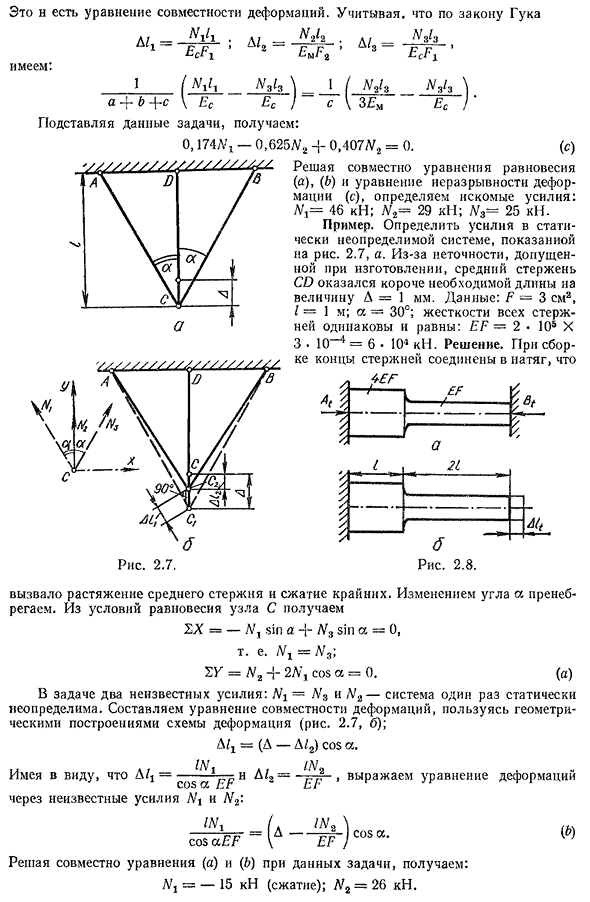
- крючка ^=- г г — ; SMG2 1 Иметь: Один. (N J i\1 / W s N3l3 ’a b\EU / C \ 3 \ m EU, заменяя эти задачи, получаем: 0.174 L-0.625 LD» +0.407 < V2=0. (После) Рис 2.7. Решите уравнения равновесия (a), ( & ) и непрерывности деформации © вместе, чтобы определить требуемую силу: L=46kN; Y2=29kN; Y3=25kN. Например. Вы также можете определить силу мышц. Определите силу в статически необнаруживаемой системе, показанной на рисунке. 2.7, A. Из-за наблюдаемой неточности в производстве средний стержень CD был короче на величину a=1 мм,
чем требуемая длина. Данные: F=3 см2, I=1 м; I=30°; определение всех стержней. При сборке конец стержня соединяется натяжением、 Это вызвало растяжение промежуточных стержней и сжатие экстремальных. Измените угол и игнорируйте. Из условий равновесия узла C получаем SX= — N r sin и N3sin и=0, то есть −3;SF=N2+2L\cos a=0. (a) эта задача имеет неизвестную силу: A’j=N3 и-система когда-то статически неопределима. Составим уравнение совместимости деформации, используя геометрическую структуру схемы деформации (рис. 2.7, b); A7g=(A—A/2) cos и…. ,, / У..
Лошадиная сила.. 1\11=~~a R n~R > используйте неизвестные силы N1 и N2 для выражения уравнения деформации: потому что АЭФ () Решая Людмила Фирмаль
уравнения вместе с(a)и (&) для этих задач, мы получаем: NT—15kN(сжатый); N2=26kN. 25 расчет напряжения, возникающего при изменении температуры в неопределенной статически системе, показан на примере. Например. Для древесины (рис. 2.8) a / 0=T\t для определения внутренних сил и напряжений в области, где температура повышается в T \ t°. Коэффициент расширения линии I/. Решение. При нагревании стержень становится удлиненным и стремится надавить на уплотнение, где происходит опорная реакция, А B/равна внутренней силе узла. Для их определения составим уравнение равновесия с-Bf=0. Это следует только
из уравнения равновесия при = Bf. Проблема не определена статически. Чтобы создать формулу совместимости деформаций, мысленно отпустите один конец балки(рис. 2.8, б). Тогда A-Z; свободно расширяется на величину=2X X3ZAZ°. Поскольку расстояние между уплотнениями не может быть изменено, под действием внутренней силы Nt той же величины, что и реакция опоры, балка должна быть уменьшена на ту же величину: А/Л = Т НЛИ N1 4. Н21 ФВ =txf-SIM0. Следовательно, N= — — — — — EFatM°. Напряжение тока температуры высчитано: (1) СП О, на первом сайте! ’= ———= 4Ф (2)АЗ О втором сайте)’ = ———= — —- Это EA * LG°» — ^- Е ТМ3,
Смотрите также:
| Расчеты на растяжение и сжатие | Расчет стержней, состоящих из разнородных материалов |
| Изгиб с растяжением (сжатием) | Чистый сдвиг |

