Оглавление:










Статически неопределимые конструкции
- Статически неопределимые конструкции Статически неопределенная структура — это структура, элементы которой невозможно определить силой, используя только уравнения статики. В дополнение к уравнениям статики для гонок- 136 страниц сто на сорок В такой системе (структуре)также необходимо использовать уравнения, связанные с деформацией элементов конструкции. Схема некоторых статически неопределенных структур показана на рисунке. 140: стержневая подвеска; B-стержень, закрепленный на обоих концах; C-кронштейн стержня; D-композитное кольцо; d-железобетон, изготовленный из бетона с включенными принадлежностями (стальные стержни). Все статически
необнаруживаемые конструкции имеют дополнительное или так называемое»дополнительное«соединение в виде крепежных элементов, стержней или других элементов. Такие связи называются излишними просто потому, что они не нужны для обеспечения устойчивости конструкции и ее геометрической инвариантности, но их формулировка не является оперативной. В условиях прочности и жесткости конструкции могут потребоваться дополнительные соединения. В статически неопределенных структурах число определяемых неизвестных больше числа статистических уравнений, которые могут быть использованы для этой цели.
Разница между числом неизвестных и числом статических уравнений определяет Людмила Фирмаль
количество дополнительных неизвестных или степень статической неопределенности в конструкции. Одна ненужная неизвестная структура называется один раз статической неопределенной, и дважды статической неопределенной, и т. д. Конфигурация показана на рисунке. 140, a, b, d-d, имеет одну дополнительную связь каждый, как только статика неопределенна, и структура, показанная на рисунке. 140, b, имеет два дополнительных соединения, что в два раза больше статического неопределенного. Решение статически неопределенной задачи. Статически неопределенная структура, элементы которой следуют в данном случае путем совместного
решения уравнений, полученных в результате учета статических, геометрических и физических аспектов задачи. 1. Обзор системы обзор системы обзор системы обзор системы обзор системы обзор системы обзор системы Контур системы подготовлены уравнения равновесия для отсекаемых структурных элементов, включая неизвестные силы. 2. Это позволяет повысить производительность вашего приложения. Устанавливают связь между деформацией или смещением отдельных элементов с учетом состояния системы в деформированном состоянии 137конструкций. Полученное уравнение называется уравнением совместимости деформаций. 3. Ф И Ч Е С К А я т о р О Н А З А Д А Н И я. на основании закона крюка
- перемещения или деформации элементов конструкции выражаются неизвестными силами, действующими на них. В случае изменения температуры, деформации, температуры добавляется к деформации, вызванной силой. 4. Решая вместе статические, геометрические и физические уравнения, мы находим неизвестные силы. Икс & ’// /. < 3 Но Отчет С П В Но Рассмотрим некоторые примеры расчетов некоторых простейших, статически неопределенных структур. 1. Осевая сила р может быть приложена к стержням, закрепленным на обоих концах (рис. 141, а). Определите силу, возникающую в нижней и верхней частях стержня. Поскольку сила Р действует вдоль оси стержня, то вертикальная составляющая реакции (RA и/?V. направим их на любой) — как показано на рисунке. 141, а. В системе сил, действующих на прямую линию, может быть создано только
одно уравнение равновесия: =Yal+Rb-P = O. (5.39) следовательно, задача когда-то статически неопределима. Это позволяет повысить производительность вашего приложения. Концы стержней жестко закреплены, так что их общая длина не изменится. И так оно и есть., А / =0. F i h i H E S K a I t o R o n A z a d a h I. В верхнем поперечном сечении действие NAc=Ra силы стержня, а в Нижнем поперечном сечении силы, используя закон NBC=-Rb-крюка, выражаем деформацию через эти силы: Как_ _ ^в * 1. ^ААБ>а эф Ф эф~эф эф(5.41) Подставляя выражение(5.41)в выражение (5.40), получаем следующее выражение: РАА БКР эф эф «в Или после сокращения до EF’. РА& = РБ^-(5.42) Если вы решите уравнение 138 (5.39) и (5.42) вместе、 _ — П А-| — Б Окончательный рисунок продольной силы показан на
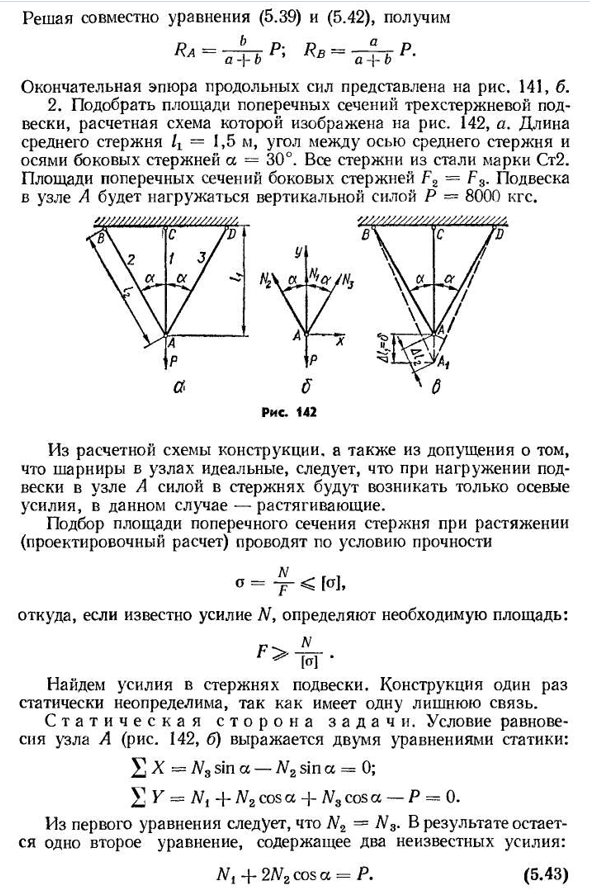
рисунке. 141, б.2. Выберите площадь поперечного сечения трех стержней подвески, расчетная схема которой показана на рисунке. 142, а. длина Людмила Фирмаль
промежуточного стержня/Т=1,5 м, угол между осью центрального стержня и осью бокового стержня а=30°. Все полюсы изготовлены из стали марки ст2. Поперечное сечение боковой панели F2=F3. Подвеска узла а снабжена вертикальной силой Р=8000кгф. Рис сто сорок два Из расчетной схемы конструкции, из предположения, что стык узла идеален, в узел нагружается подвеска, а усилие в стержне генерирует только осевое усилие. Выбор площади поперечного сечения стержня при растяжении (расчетный расчет) осуществляется в соответствии с условиями прочности o= — y — <и » здесь, если мы знаем силу 7V, мы определяем необходимую площадь: Найдите
силу тяги подвески. Он имеет одно дополнительное соединение, поэтому структура когда-то статически неопределима. Система система система система система резюме резюме резюме резюме резюме резюме резюме резюме Резюме система система система система система система система система резюме резюме резюме Резюме сбалансированности узла а(рис. 142, б) представляется двумя статическими уравнениями: Y, X=2V3sin a-N2sin a=0; Y, V=Nt+N2cos a+N3cos a-P-0. Из первого уравнения следует N2—N3. В результате получается одно второе уравнение, содержащее две неизвестные силы: Aff4-2 / V2 cos a=P(5.43) 139G e o m e T R I h E s K A I S t o R o n A
z a d A h I. Поскольку система симметрична относительно оси центрального стержня, а боковые стержни растягиваются с одинаковой силой, то при деформировании подвески узел A имеет определенное значение 6. Отображает положение нового узла(рис. 142, в). Все стержни будут длиннее и в положении, указанном на схеме. 142, с ломаными линиями. Расширение среднего стержня, очевидно, D/g=b. Удлинение поперечного стержня связано с тем, что из точек B и D, где радиус равен VA (или OL), проводят дугу через точку A, а упругое удлинение очень мало по сравнению с длиной стержня B/li и DAt при внесении засечек на новую длину
стержня(рис. 142,при котором рост видимости сильно возрастает), можно считать, что между углом и осью планка не изменяется, а выполняется дуга для замены перпендикуляра, завязывания и далее, как видно из фотографии., D/3=D / 2=D / {cos a. (5.44) удлинение стержней представлено законами крючка силами, действующими на них: D/,= -^ -; D/2=. (5.45 )) С и н т е с. подставляя значения D/x и D / 2 в выражение (5.45) — ^=4^ — потому что.(5.46) Равнина N на L、\: Ее., А^коза, Или П2=соз а,(5.47) И 1 ФВ Где q= — y-2 -, C2= — средняя жесткость и H*2 соответственно Боковые стержни. Добавление
выражения(5.47)к выражению(5.43)дает JVt+2/V, cos2a=P, И 1 Откуда М= — — — — — — — — Г———• (5.48) 1Н-2-cos2a вопрос Прочитайте выражение 140 (5.47) и получите N2: П-потому что Н2= — — — — — — — С2————. (5.49) 1+2-cos2a q Усилия L\и L^2 зависели от соотношения жесткости стержня. Поэтому при расчетах конструкции ее можно рассчитать только путем указания коэффициента жесткости. Это одна из особенностей статически неопределенных расчетов стержневых систем. Для того же материала стержень задается не отношением жесткости, а отношением площади поперечного сечения, которое устанавливает определенное отношение жесткости стержня. Затем, если вы укажете lx=/2cosa, вы получите * 2 C2_^2^1_ff2l22cos a_cos A Q l3EFl l2EFJi k Силы
тяг N1 (5.48) и N2 (5.49) определяются такими формулами: НТ=——Ф;(5.50)) 1+ — cos8a АРИЗОНА P cos2a™2~L+2cos8a ’ (5.51) Мы рассчитываем эти усилия, принимая, например, k=2: £000 1+0,8663 =4850kgs; ,, _8000•0,8662 2(1+0,8668) =1820кгф. Выберем площадь поперечного сечения стержня, исходя из предположения, что напряжение промежуточного стержня равно допустимому диапазону Yu[o]=1400кгф / см2. Затем F— 4 8 5 0 1M1400 см2=см2 и 3.46. Площадь поперечного сечения боковых стержней, согласно принятому соединению, получаем:: = 4 «= −2 » = ’7 3 cm2-напряжение, при котором работают эти стержни, OI=o/ / / =kgf / cm2=1050kgf / SMA; Г2 1, / о 141 это напряжение меньше допустимого напряжения, то есть стержень имеет избыточный запас прочности. Определите
площадь поперечного сечения поперечного стержня Fz из условий прочности, а затем, в соответствии с допустимым соотношением, примите Fx=(2F2, напряжение промежуточного стержня будет больше допустимого. Поэтому этот второй вариант выбора площади поперечного сечения следует отбросить. Заметим, что в рассматриваемой статически неопределенной структуре невозможно уравнять прочность всех элементов. Начальные и термические напряжения. Свободная сборка статически неопределенных систем возможна только при высокоточном изготовлении элементов. В противном случае сборка будет принудительной Райс сто сорок три Для того чтобы осуществить с применением силы вызывающую деформацию элементов в них после монтажа системы, следовательно, возникает давление, называемое
первым или монтажным. В статически определяемой конструкции размерная неточность элемента не требует приложения усилия во время монтажа, и начальное напряжение на элементе не возникает. В элементах статически неопределенной системы Сила и давление также возникают при изменении температуры. Стержень прочно закреплен между двумя стенками, а на конце Б-на телевизоре в конце его температура повышается на 7Д, причем по длине стержня она фиксируется по закону. Т(ч)=7Д+ХП. (5.57)) При N=0 изменения температуры по длине стержня постоянны, равны ТВ, а при n=1 температура изменяется линейно при n=2, согласно закону вторичной параболы. Определим реакцию фиксации и напряжения в стержне. Обзор системы обзор системы обзор системы обзор
системы обзор системы обзор системы обзор системы обзор системы обзор системы, так как температура системы повышается, стержни, как правило, удлиненная. Этому препятствует жесткая опора, в результате чего вдоль оси стержня происходит реакция(рис. 144). В системе сил, направленных на прямую линию, можно составить уравнение равновесия:£x=/?л-я в = о, Откуда РА-РБ = Я(5.58) Таким образом, проблема однажды статически не определена. Осевая сила в стержне N=R. Это позволяет повысить производительность вашего приложения. Благодаря креплению конца стержня, его длина не изменяется: Д/=0. (5.59) 144F I h i h E s K a t o R o n A z a d a h I. укорочение свободного стержня, вызванное продольными силами, равными реакции крепления, =(5.60) Удлинение свободного стержня при нагревании определяется следующим
образом. На расстоянии x от конца стержня A выбирают элемент длины dx, где повышение температуры T (x) считается постоянным. Температурное удлинение этого элемента Adxr=(x) dx=a^G A+ — CP^dx. Температурное удлинение всего стержня определяется интегрированием формулы (5.61) по длине стержня: d / g=/» (» — + (5.61) ТВ \ п+1ДЖ Общее изменение длины стержня составляет M=d/L. 4 — — — F — +al I \ TL+ * <5-6 3>n t e Z. подставим формулу (5.63) в Формулу (5.59)-. (5.62) С и Лучом Откуда — &+«’(7’и+4dc не) -«. Найти опору для реакций: (5.64) Я (5.65) И напряжение тока: Ах= (5.66)) N » Я? Я т р~т\р^ — а[т л+ — т Т Г -] Е. При N=0 Последние два уравнения входят
в уравнение для равномерного нагрева стержня по длине at-R-Alt EF и I-AEMG MG=T. Рассмотрим численный пример. Определить осевое усилие и напряжение стального стержня I=80 см; F=20 см2; E=2X x10E кгс / см2;a=125*10-7;TL=10°; G»=55 ° C. Температуру по длине стержня определяют по температуре вторичной параболы (Р-2). Назначьте числа формулам(5.65) и (5.66), чтобы найти N= ~ 125-10″7 (1 0 + ^ = 2 ° — ) 2 • 10E•20kgs= — 12500kgs, N12500 а=р= — GQ в-кгс / см2= — 625 кгс / см2. Обратите внимание, что по мере снижения температуры в системе, как показано на рисунке 145, температура падает. 144, происходит растягивающее напряжение. На основе примеров, рассмотренных в настоящем пункте, отмечаются следующие особенности статически неопределенной структуры, отличные от тех, которые могут быть статически определены:1. Распределение сил между элементами статической неопределенной конструкции зависит от жесткости этих
элементов. Если вы увеличите жесткость любого из них, то вам потребуется больше усилий. Изменяя соотношение жесткости элементов конструкции, можно изменять распределение их сил любым способом. 2. В статически неопределенных конструкциях сила и напряжение возникают, когда температура элемента изменяется по сравнению с температурой, при которой происходит сборка конструкции. 3. В элементе статически неопределенной структуры могут существовать силы и напряжения при отсутствии внешних сил. Эти силы и напряжения, называемые начальными (сборочными)
, возникают в процессе сборки конструкции. Начальное напряжение создается с определенной целью (например, затяжка болтов, прижимная посадка) или в результате неправильного изготовления отдельных конструктивных элементов. 4. В статически неопределенных конструкциях, как правило, невозможно одновременно получить на всех элементах напряжения, равные допустимым. При проектировании такой конструкции это следует иметь в виду.
Смотрите также:
| Вычисление напряжений и деформаций. | Расчет гибких нитей |
| Учет собственного веса и сил инерции | Расчет винтовых цилиндрических пружин |

