Оглавление:




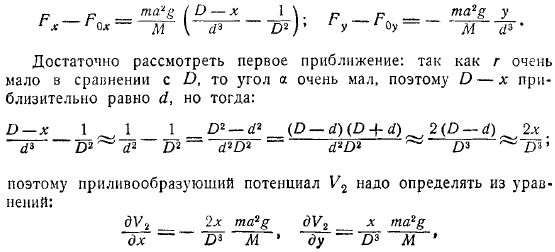


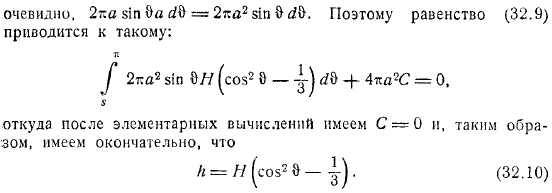

Статическая теория приливов
Примените предыдущий вывод к теории приливных течений. Во-первых, мы вводим статическую теорию так называемой приливной статики. Его основателями являются Ньютон и Даниэль Бернулли. Эта теория гидромеханики, по сути, гидростатического и изгибы фигуры явление приливов только в общих чертах.
Теория приливов основана на предположении, что в любой момент океан, покрывающий землю, находится в равновесии под действием силы тяжести и основан на возмущающих силах, возникающих от Луны и солнца. Таким образом, свободная поверхность воды принимает форму плоской поверхности. Где в каналах постоянной глубины есть возможность всех сил, действующих на жидкость.
- Рассмотрим только возмущающее тело, например Луну. Точно так же учитывается влияние Солнца, а общее влияние Луны и солнца принимается как сумма эффектов, которые они оказывают по отдельности.
- Во-первых, мы предполагаем, что нет никакого беспокоящего тела.
Указывает на возможность гравитации (в том числе центробежной силы вращения Земли). Людмила Фирмаль
Здесь сферические координаты точки обозначаются через расстояние до центра Земли, широту точки, западную долготу. Уравнение поверхности океана при отсутствии обструктивных объектов.
Далее поверхность моря должна быть горизонтальной поверхностью, поэтому вам нужно. На это также указывают потенциальные приливные силы. Наличие Луны, уравнение уровня моря уже есть. А все потому что возможности сил действующих на море сейчас есть. Выглядит так.
- На самом деле, смещение массы воды, которая составляет океан, изменяет гравитационный потенциал, но это изменение игнорируется. Если в статической теории приливов вычесть уравнение из этого уравнения, то оно выглядит так.
- Из-за малой высоты прилива по сравнению с ним, функция может быть в дальнейшем просто заменена на средний радиус Земли.
Вдоль земного радиуса существуют составляющие силы, действующие на единицу массы. Таким образом, в итоге мы получаем следующие основные уравнения статической теории течения. Вы можете рассчитать высоту уровня прилива.
Расчет силы прилива остается прежним. Людмила Фирмаль
Примечание: расстояние от центра Земли до Луны. Угол, образованный радиус-вектором, проведенным в точке жидкости через расстояние от Луны до рассматриваемого объекта.
Точка, через которую нужно пройти, масса Луны, через которую нужно пройти, масса Земли, через которую нужно пройти, радиус Земли, через который нужно пройти. Тогда сила притяжения к Луне, действующая на единицы массы, находящиеся в ней, определяется из следующих соотношений. Сила притяжения прямо пропорциональна массе притягиваемого объекта, и обратно пропорциональна мощности расстояния между ними.
На некоторое время возьмите координатные оси и нарисуйте их, как показано на рисунке. В этом случае проекция сил на координатные оси очевидно. Чтобы вычислить силу на единицу массы, проекция ускорения частиц жидкости, вызванного притяжением Луны, также будет одинаковой.
Но если предположить, что землю можно считать состоящей из однородных слоев сферической формы, то при расчете влияния Луны на твердую землю последняя действует на всю Землю, то ускорение, передаваемое всей Земле Луной, определяется по формуле. Поскольку рассматривается только смещение частиц жидкости относительно глобуса, то кажущаяся сила — это явно только разница. Достаточно рассмотреть первое приближение.
Поскольку углы очень малы, углы очень малы, поэтому они примерно равны, но они могут быть. Поэтому потенциал формирования потенциала следует определять по следующей формуле. И замените y формулой, она в конечном итоге будет выглядеть так.
Обратите внимание на то, что сила приливной силы пропорциональна массе возмущающего объекта и обратно пропорциональна степени расстояния от последнего до возмущающего объекта, так что сила приливной силы Луны больше, чем сила приливной силы Солнца. Применяя основное уравнение статической теории приливов, получаем следующее уравнение для высоты прилива. При этом заменяется среднее значение радиуса Земли.
Для простоты приведу обозначения формула для потенциала принимает следующий вид, и уравнение может быть записано в виде. Остается определить константу с из условия, что объем жидкости не изменяется после деформации, произведенной мешалкой. Это условие, по-видимому, представлено равенством Распространяется по всей поверхности земли (для простоты будем считать, что вся земля покрыта океаном).
Разделите всю поверхность Земли на полосы. Каждая полоса заключена в небольших круга, которые соответствуют соседним значениям. Круг — это явно пересечение Земли и плоскости, перпендикулярной линии.
Площадь таких полос должна быть. Очевидно. Поэтому равенство Сводится к этому. И затем основной расчет делается оттуда, так что в конце концов.

