Оглавление:
Стандартные задачи и схемы их решения
В частности, на методе возведения в степень основано решение многих весьма распространённых видов иррациональных уравнений и неравенств. Обратимся к стандартным схемам их решения.
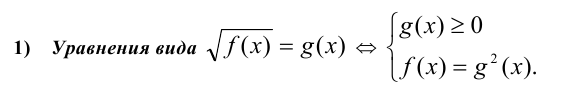
Пример №226.
Решить уравнение
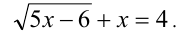
Решение:
Перепишем уравнение в виде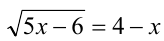 
,
и затем воспользуемся указанной схемой решения:
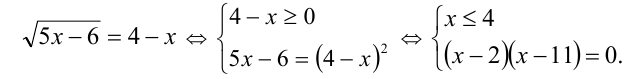
Ответ: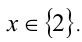 
Пример №227.
Решить уравнение
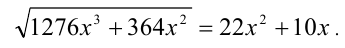
Решение:
Прежде всего, заметим, что обе части уравнения можно сократить на 2:
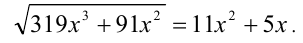
Действуя далее по схеме, получаем, что уравнение равносильно системе
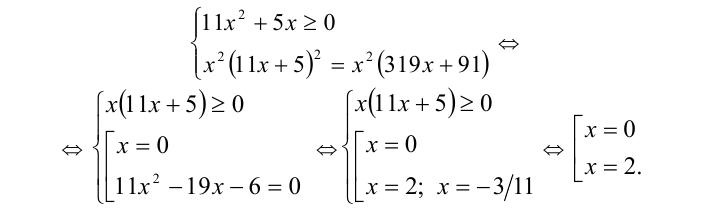
Пример №228.
Решить уравнение
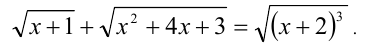
Решение:
Пусть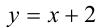
, тогда при 
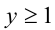уравнение принимает вид 
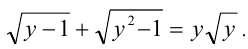Уединив более «сложный» корень, приведём уравнение к виду
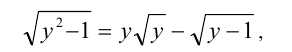
и воспользуемся приведенной выше схемой
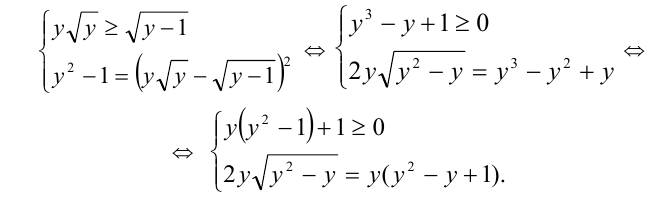
Неравенство системы выполнено при всех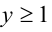 
, поэтому, сократив уравнение на у , получим 
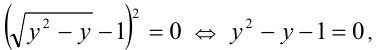откуда с учётом 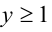находим 
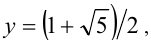т.е.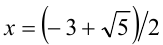 
единственное решение.
Ответ: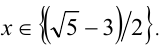 
2) Неравенства вида
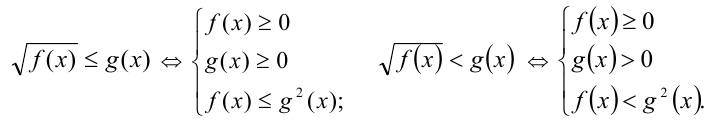
Пример №229.
Решить неравенство
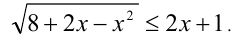
Решение:
Согласно схеме неравенство равносильно системе
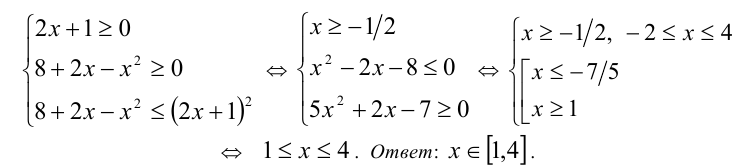
Пример №230.
Решить неравенство
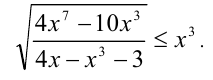
Решение:
Заметим, что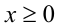 
, причём 
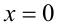— решение. Найдём другие положительные решения неравенства. Имеем
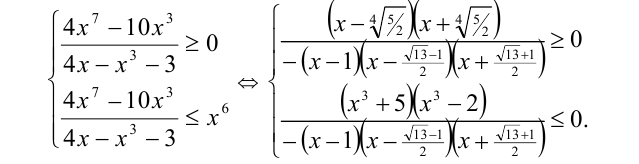
Решая каждое из неравенств методом интервалов, получим
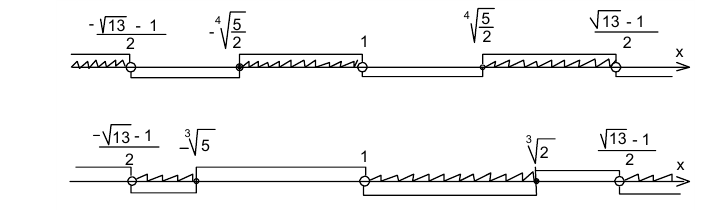
Таким образом, приходим к ответу: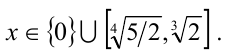 
.
3) Неравенства вида
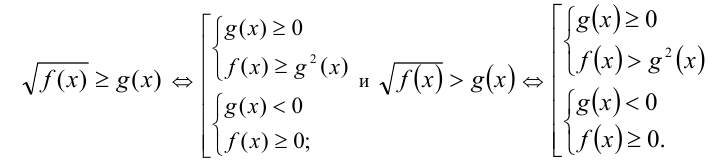
Эта ссылка возможно вам будет полезна:
Пример №231.
Решить неравенство
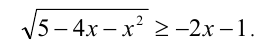
Решение:
Согласно схеме, неравенство равносильно совокупности
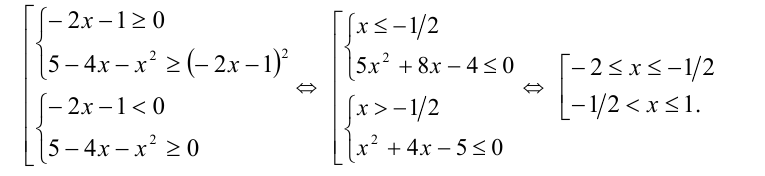
Ответ: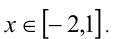 
Отметим, что, вообще говоря, не все неравенства указанного вида удобно решать с помощью предложенной схемы. Приведём два примера, когда целесообразнее воспользоваться стандартным подходом, учитывающим ОДЗ.
Пример №232.
Решить неравенство
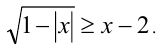
Решение:
ОДЗ: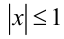 
. Но тогда выражение в правой части неравенства отрицательно и, следовательно, неравенство верно всюду на ОДЗ.
Пример №233.
Решить неравенство
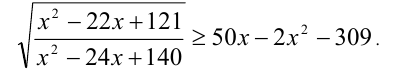
Решение:
ОДЗ:
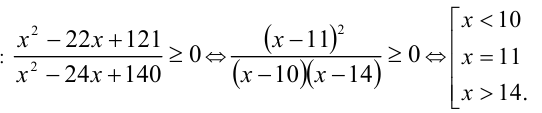
Заметим, что правая часть неравенства отрицательна на ОДЗ, в самом деле,
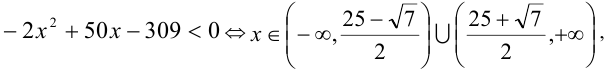
причем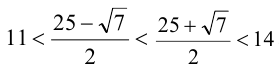
Итак, исходное неравенство верно при всех x из ОДЗ.
Ответ: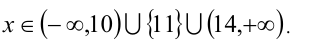 
4) Уравнения вида
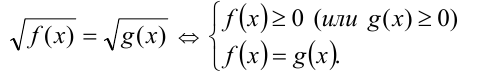
Пример №234.
Решить уравнение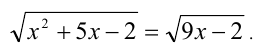 
Решение:
Согласно схеме, данное уравнение равносильно системе
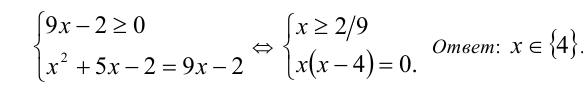
5) Неравенства вида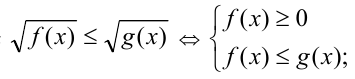 
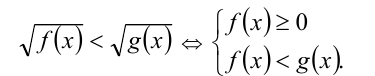
Пример №235.
Решить неравенство
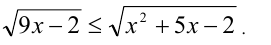
Решение:
Согласно схеме, неравенство равносильно системе
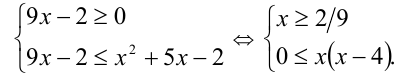
Ответ: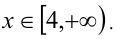 
Пример №236.
Решить неравенство
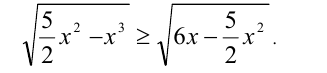
Решение:
Неравенство равносильно системе
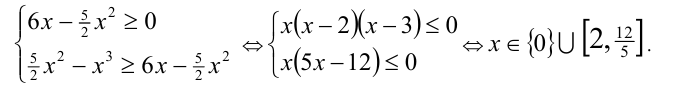
6) Уравнения вида
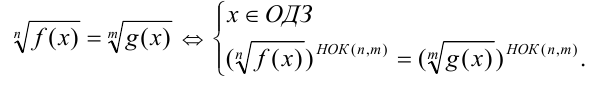
Пример №237.
Решить уравнение
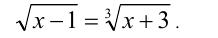
Решение:
Перейдём от уравнения к равносильной ему системе
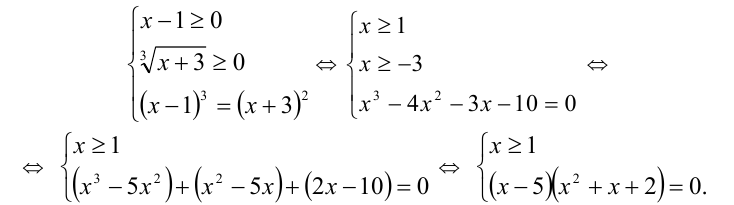
Ответ: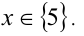 
Пример №238.
Решить уравнение
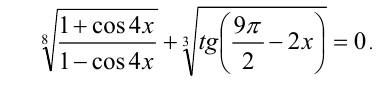
Решение:
Упростив подкоренные выражения, приведём уравнение к виду
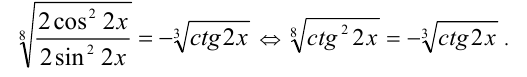
Сделав замену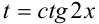 
, приходим к алгебраическому уравнению и решаем его:
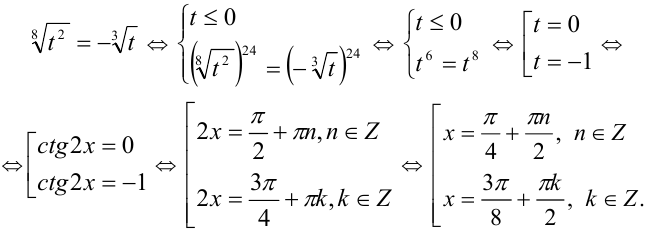
7) Неравенства вида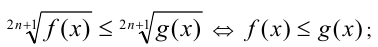 
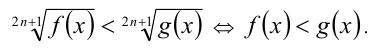
Пример №239.
Решить неравенство
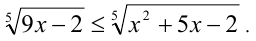
Решение:
Возводя в пятую степень, получаем равносильное неравенство
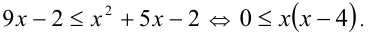
Ответ: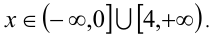 
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
