Пример задачи 4.1
Стальной стержень круглого поперечного сечения (рис. 4.6) находится под действием скручивающей нагрузки (моментов 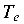 ).
).
Определить диаметр стержня из условий прочности и жесткости. Для материала стержня 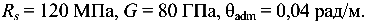
Решение
Как следует из условия примера, стержень подвергается деформации кручения.
На расчетной схеме (рис. 4.7) выбирается начало координат (крайнее левое сечение) и положительное направление продольной оси Z; назначаются расчетные участки с границами в сечениях, где приложены скручивающие моменты 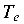 . Длинам участков придается индекс номера участка. В пределах расчетных участков намечаются поперечные сечения (I-III) и отмечается их положение в системе координатной оси
. Длинам участков придается индекс номера участка. В пределах расчетных участков намечаются поперечные сечения (I-III) и отмечается их положение в системе координатной оси 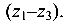
Исходя из характера нагрузки к стержню может быть применено только одно уравнение равновесия 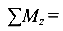 0, из которого определим значение момента
0, из которого определим значение момента 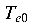 .
.
Уравнение равновесия
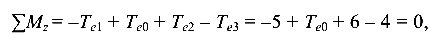
откуда 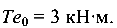
Определим крутящие моменты Т на участках стержня, используя ранее описанный способ:
1) участок 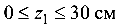 :
:
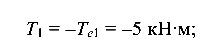
2) участок 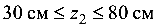 :
:
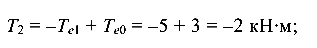
3) участок 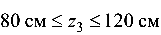 :
:
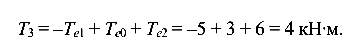
При сосредоточенной нагрузке значения крутящих моментов Т не зависят от ординаты Z и, следовательно, являются постоянными в пределах расчетных участков 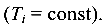
По полученным значениям Т в выбранном масштабе строится эпюра крутящих моментов (рис. 4.7, б). Из эпюры максимальный крутящий момент 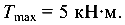
Из условия прочности по касательным напряжениям (4.2) определяем диаметр стержня:
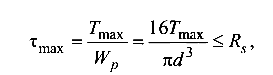
откуда
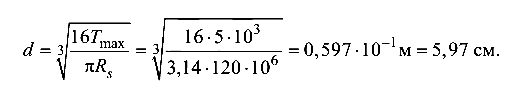
Из условия жесткости (4.4)
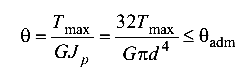
диаметр стержня

Из двух значений d выбираем большее и, с учетом стандарта, принимаем d=6,5 см.
Деформации (углы закручивания на участке стержня определяются по формуле (4.3):
на участке стержня определяются по формуле (4.3):
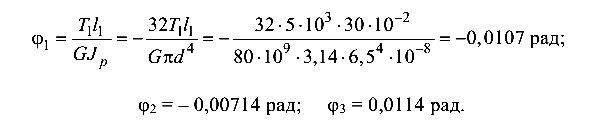
Полученные значения углов закручивания  позволяют вычислить перемещения граничных сечений стержня и построить эпюру перемещений. Крайнее левое сечение О примем за относительно неподвижное:
позволяют вычислить перемещения граничных сечений стержня и построить эпюру перемещений. Крайнее левое сечение О примем за относительно неподвижное: 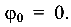 Перемещение последующих граничных сечений будет равно алгебраической сумме углов закручивания участков, расположенных с начала отсчета:
Перемещение последующих граничных сечений будет равно алгебраической сумме углов закручивания участков, расположенных с начала отсчета:
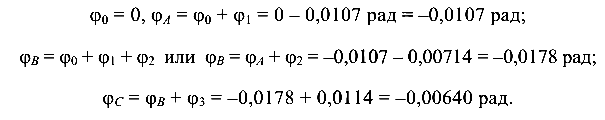
Эпюра перемещений показана на рис. 4.7, в.
Наибольшее касательное напряжение будет на первом участке стержня, где 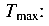
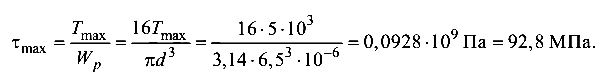
Эпюра распределения касательных напряжений по поперечному сечению и угол поворота приведены на рис. 4.7, г.
Анализ результатов вычислений
На эпюре крутящих моментов в граничных сечениях имеются «скачки», равные значениям скручивающих моментов.
Наиболее нагружен первый участок стержня 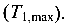 Здесь и наибольшие касательные напряжения
Здесь и наибольшие касательные напряжения
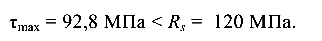
Материал стержня значительно недонапряжен, так как диаметр стержня принят не по условию прочности, а по условию жесткости, которое оказалось более требовательным.
Наибольший относительный угол закручивания будет на третьем участке:
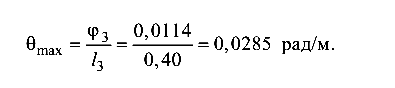
Из эпюры перемещений видно, что наибольшее перемещение претерпевает сечение В, в котором  = 0,0178 рад.
= 0,0178 рад.
Этот пример решения задачи взят со страницы решения задач с примерами по всем темам предмета «Сопротивление материалов»:
Примеры решения задач по сопротивлению материалов
Дополнительные задачи которые вам будут полезны:
