



- Якоб объяснил несколько способов решения проблемы устойчивой теплопроводности. Рассмотрим только метод релаксации, который является простым, но мощным инструментом. Хотя этот метод используется во многих областях науки и техники, он ограничивается его применением для решения задач теплопроводности. Сначала рассмотрим применение релаксационного метода к 1D тепловому потоку. Система показана на рисунке. 22.1 является твердым телом с температурной стабильностью .
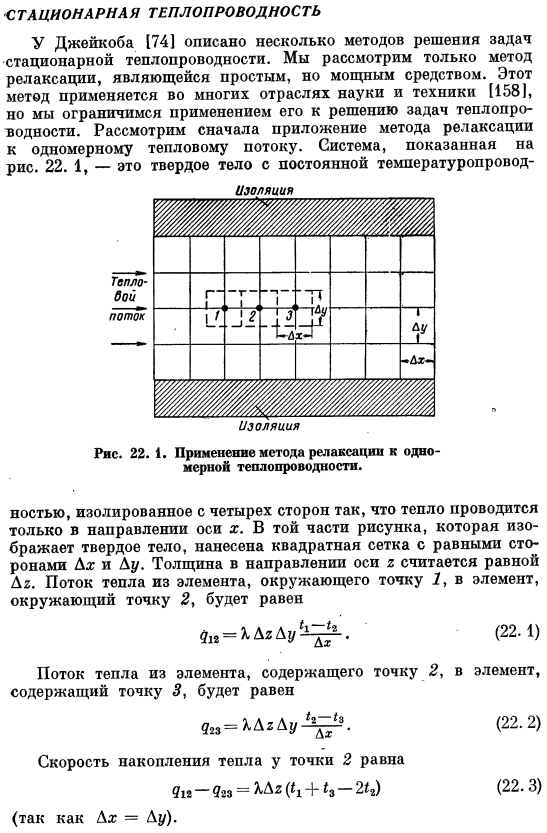
Изолированно. Рисунок 22. 1. Применение метода релаксации к 1-мерной теплопроводности. Он изолирован с 4 сторонами так, что жара будет дирижирована только в направлении x-axis. In в той части рисунка, которая представляет собой твердое тело, применяется квадратная сетка со сторонами, где Lx и Du равны. Толщина в направлении оси 2 считается равной Dg. Тепловой поток от элемента, охватывающего точку 7, к элементу, охватывающему точку 2、 912 = ДГ до Ду.
Тепловой поток от элемента, содержащего точку 2, к элементу, содержащему точку 5, равен、 529 = XD2Dr/ -^. (22.2) Скорость аккумулирования тепла в точке 2 равна Un-У2= = ХД2-мз2-мз2) (22.3) (Дл: = Ду).Формула (22. 3)также может быть записан в следующем формате: ^ 14 ″ −2 * А. (22. 4. Если система находится в стационарном состоянии, то d12 равно d23, и уравнение 22.
Может быть преобразован следующим образом: 2 = 14к — ’ (22.5) Если для всех точек системы выбрано какое-либо распределение температуры, то его можно проверить по формуле (22.5).Если температура 12 выбрана неправильно, ее можно исправить путем добавления или вычитания из температуры( Начальные значения 1\, 1h и заданное значение имеет температурный размер, добавляя его к уравнению (22. 5) удовлетворяйтесь каждый раз в пункте 2.Температура нарушает соответствие между температурой других точек. Однако значение коррекции уменьшается наполовину по мере движения к соседней точке, и если оно изначально не слишком велико, то сразу уменьшается до незначительного значения.
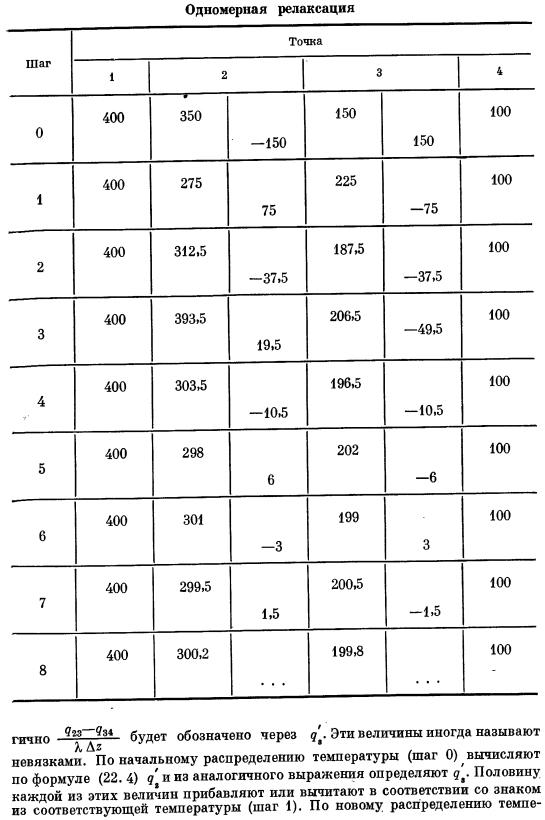
Методы смягчения последствий показаны в Примере 22.1. Пример 22.1 Тепло передается от источника тепла с температурой 400°С к теплоотводу с температурой 100°С через твердый стержень. Сторона стержня изолирована, как показано на рисунке. 22. 2.Найти распределение Изоляция 22.1). Температурное разделение стержня. Используя закон теплопроводности Фурье, мы обнаружили, что распределение температуры в стержне становится линейной функцией координат. Однако, чтобы проиллюстрировать этот подход, мы предполагаем, что точка 2 имеет температуру Aao C, а точка 3 имеет температуру 150°C. Вы можете выполнить расчеты, как показано в таблице. 22. 1.Значение. ^ 53 указывается вопрос、 Шаг точки 1, 2, 3, 4.
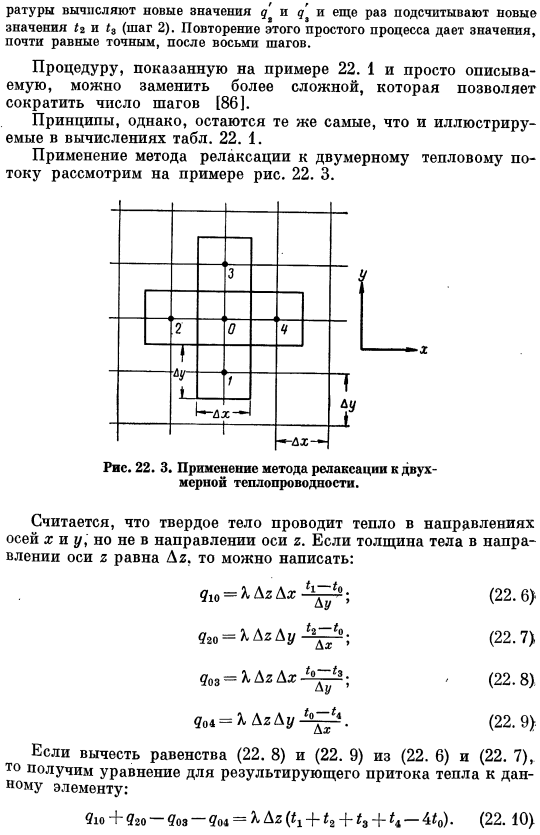
Половина каждого из этих значений складывается или вычитается в соответствии со знаком из соответствующей температуры (Шаг 1).Используя новое распределение температуры, вычисляются новые значения d ’и d’ и снова подсчитываются новые значения/ 2 и / 3(Шаг 2).Если вы повторите этот простой процесс, то после 8 шагов вы получите точно приблизительно равные значения. Пример 22. Процедура, которая показана на рис. 1 и кратко описана, может быть заменена более сложными процедурами, сокращающими число шагов[86]. Однако принцип тот же, что указан в расчетной таблице. 22.1. Применение релаксационного метода к двумерному теплу. Рисунок 22.
- Применение релаксационных методов к 2 видам измеряется теплопроводность. Считается, что твердые тела проводят тепло в направлениях оси x и оси y, но не в направлениях оси Z. Если толщина объекта в 2-осевом направлении равна Dg, то ее можно описать следующим образом: d10 =%DgDx — ^ 2; (22.6} 9r0 = XD2D1/ -^ -«; (22.7) 9 унций= XD2Dr -^;, (22,8) вы. Ц4 = KDgDr -^». (22.9)} (22. 6) и (22. 7) из равенства (22. 8) и (22. 9) вычтите и вы получите уравнение притока тепла к конечному элементу. 9×4 «?20#03 =(^ 1 4〜^ 2» b ^ 3 4 — ^ 4 ^ 4 ^ d).(22. 10) как и раньше, kx равно Dy, поэтому эти значения уменьшаются. 22.10) определите значение в выражении.
Если процесс теплопередачи стационарный, то y0 равно нулю и среднему арифметическому температуры в 4 соседних точках. 50°C. найти температуру среды Пример 22.2 Внутренняя температура стенки печи составляет 200 ° C, а внешняя это настенный провод. Стена показана на рисунке. 22. 4. квадратная сетка, где стороны равны половине толщины стенки. Точка 4a имеет ту же температуру, что и точка 4 из-за плоскости симметрии, проходящей через corner. At на значительном расстоянии от угла, температура в середине стены, очевидно, будет 125°C. Если 125°C, очевидно, возникает ошибка. Это связано с тем, что точка 5 требует более низкой температуры.
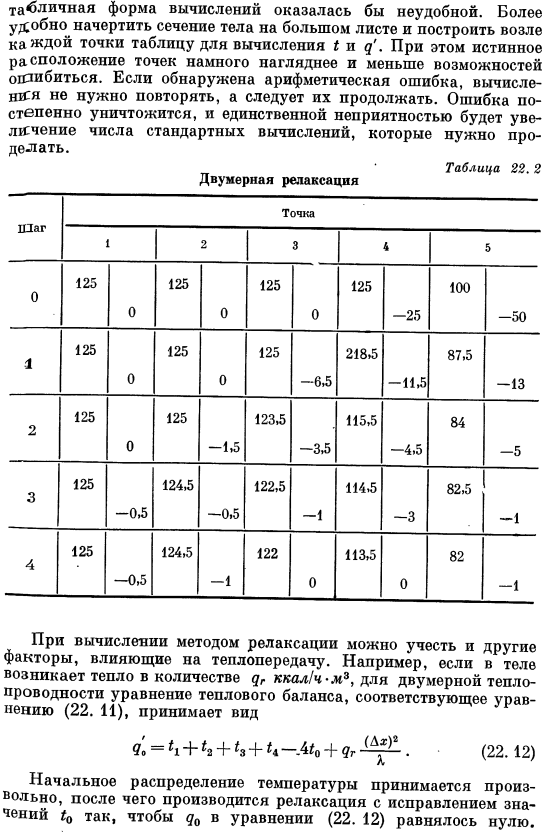
Следовательно= = 100°С、11 =(2 = = 4 = = 125°C. Таблица обеспечивает решение проблемы. 22.2.Используемый метод заключается в вычислении значения d ’с использованием распределения температуры. Например, найдите в шаге 0 d’b = 125 + 50 + 504-125-4-100 = −50 и −125 + 50 +100 + 200-4•125 = −25 и другие. Затем, чтобы получить новый температурный профиль, вычисление повторяется до тех пор, пока значение D ’не станет незначительным, причем 4 минуты 1 из d’ добавляются или вычитаются к каждому соответствующему значению температуры. Точность значений температуры в Примере 22.2 может быть улучшена с помощью более тонкой сетки.
Если границы стен изогнуты, то вам действительно понадобится более тонкая сетка. Однако температура, найденная в грубой сетке, служит хорошей основой для выбора начального распределения температуры в более мелкой сетке. grid. In пример 22.2, существует 2-сторонний тепловой поток, но расчет упрощается тем, что точка, где определяется температура, лежит на 1 Прямой линии. Для более тонкой сетки процесс температурной «релаксации» должен выполняться в обоих случаях directions. In в этом случае табличная форма расчета, показанная в примере, является inconvenient. It удобнее нарисовать часть тела на большом листе и создать таблицу возле каждой точки для вычисления I и q.
В то же время истинное положение точки становится более ясным и меньше шансов ошибиться. Если обнаружена арифметическая ошибка, то повторять вычисление не обязательно, но необходимо продолжить. Ошибки постепенно уничтожаются, и единственная неприятность-это увеличение количества стандартных вычислений, которые необходимо выполнить. Таблица 22. Два Двумерная релаксация Точки Шаг 1 2 3 4 5 0125 0125 0125 0125-25-25-100-50 1125 0125 0125 −6.5 218.5 -Ил 87.5-13 2125 0125 −1.5 123.5 −3.5 115.5 −4.5 84 −5 3125 −0.5 124.5 −0.5 122.5 −1 114.5 −3 82.5 −1 4125 −0.5 124.5 −1 122 0 113.5 0 82 −1 Расчет методом релаксации позволяет учесть и другие факторы, влияющие на теплообмен.
Например, в случае 2-D теплопроводности, если тепло возникает в организме в количестве dg ккал / ч-м3, формула (22. 11) соответствующее уравнение термического распада принимает вид: 0″ = — ха+ * 3 + —Al0 4-dg. (22.12) Начальное распределение температуры берется произвольно, а затем по формуле (22. 12) релаксация выполняется с поправкой 10 так, что g0 равно 0, и 3-мерная теплопроводность также может быть рассмотрена методом релаксации. В трехмерной сетке каждый внутренний узел окружен 6 точками. Форма уравнения релаксации (без тепловыделения) имеет вид ^ 2 ″ мс «м *» б » б (22. Тринадцать) В выбранном примере температура границы твердого тела была известна.
Однако, если твердая поверхность находится в контакте с жидкостью, температура жидкости обычно известна. Этот тип задач может быть решен релаксационными методами, но требует использования коэффициентов теплопередачи, которые еще не были рассмотрены. Эта методика достаточно проста, и после изучения коэффициента совместного конвективного теплообмена читателю представляется вывод соответствующего уравнения релаксации. Для некоторых целей распределение температуры в организме может быть независимым вопросом, но чаще всего оно используется для расчета тепла.
Смотрите также:
| Правило Ньюмена | Нестационарная теплопроводность |
| Численные, графические и аналоговые методы в исследовании теплопроводности | Аналоговые методы |
