Оглавление:
Сравнение действительных чисел. Арифметические операции над действительными числами и их свойства
Два действительных числа 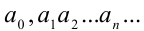 и
и 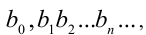 где
где 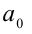 и
и 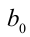 -целые числа, а
-целые числа, а 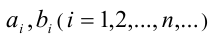 — десятичные цифры, называются равными, если
— десятичные цифры, называются равными, если 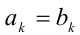 сразу при всех
сразу при всех 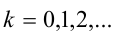 Равными также являются числа
Равными также являются числа
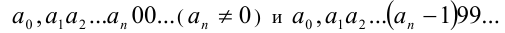
(это две эквивалентные формы представления одного и того же действительного числа 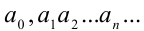 ). В дальнейшем договоримся рассматривать только первую из двух приведённых форм представления периодических дробей (с периодом 0).
). В дальнейшем договоримся рассматривать только первую из двух приведённых форм представления периодических дробей (с периодом 0).
Положительную бесконечную десятичную дробь назовём положительным действительным числом, отрицательную бесконечную десятичную дробь — отрицательным действительным числом, нулевую бесконечную периодическую дробь (с периодом нуль) — числом нуль. Любое положительное действительное число больше нуля, а любое отрицательное действительное число — меньше нуля (и меньше любого положительного числа).
Введём для двух положительных действительных чисел операцию сравнения. Говорят, что из двух чисел 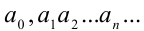 и
и 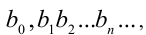 первое больше второго, если либо
первое больше второго, если либо 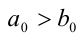 , либо если
, либо если 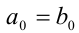 , но
, но 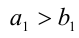 , либо если
, либо если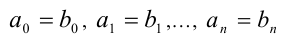 (для некоторого натурального n), но
(для некоторого натурального n), но 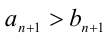 .
.
Два действительных числа 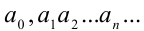 и
и 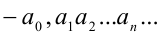 называются противоположными числами. Два отрицательных действительных числа равны, если равны противоположные им числа. Из двух отрицательных чисел больше то, у которого противоположное число меньше.
называются противоположными числами. Два отрицательных действительных числа равны, если равны противоположные им числа. Из двух отрицательных чисел больше то, у которого противоположное число меньше.
На множестве действительных чисел также определены четыре основные арифметические операции: сложения, умножения, вычитания и деления, причём арифметические операции над действительными числами удовлетворяют тем же законам коммутативности, ассоциативности и дистрибутивности, что и над рациональными числами.
Рассмотрим, например, как определяется понятие суммы. Суммой двух произвольных действительных чисел а и b называется такое действительное число c, которое удовлетворяет неравенству
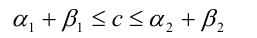
сразу для всех рациональных чисел 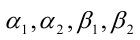 , таких, что
, таких, что
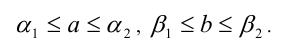
Такое число c всегда существует и единственно (доказывается в курсе высшей математики).
Произведением двух положительных действительных чисел а и b называется такое действительное число c, что неравенство
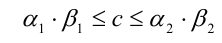
выполняется для всевозможных рациональных 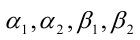 удовлетворяющих неравенствам
удовлетворяющих неравенствам 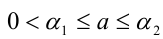 ,
, 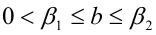 . Такое число c также всегда существует и притом только одно. Произведение двух отрицательных действительных чисел определяется как произведение противоположных им положительных чисел. Произведение двух действительных чисел разных знаков
. Такое число c также всегда существует и притом только одно. Произведение двух отрицательных действительных чисел определяется как произведение противоположных им положительных чисел. Произведение двух действительных чисел разных знаков 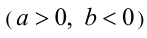 равно взятому со знаком минус произведению числа а на число, противоположное b . Это отрицательное число существует и единственно (аналогично определяется произведение
равно взятому со знаком минус произведению числа а на число, противоположное b . Это отрицательное число существует и единственно (аналогично определяется произведение 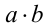 в случае
в случае 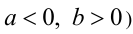 . Произве-дение двух чисел, одно из которых есть нуль, равно нулю. Значение числа не меняется при умножении его на единицу.
. Произве-дение двух чисел, одно из которых есть нуль, равно нулю. Значение числа не меняется при умножении его на единицу.
Для действий сложения и умножения действительных чисел вводятся обратные действия — вычитание и деление. Вычесть из действительного числа а действительное число b означает найти действительное число c такое, что 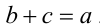 . Разделить действительное число а (делимое) на отличное от нуля действительное число b (делитель) значит найти действительное число c (частное) такое, что
. Разделить действительное число а (делимое) на отличное от нуля действительное число b (делитель) значит найти действительное число c (частное) такое, что 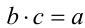 . Это всегда можно сделать, притом единственным образом. Множество действительных чисел замкнуто относительно введённых четырёх арифметических операций.
. Это всегда можно сделать, притом единственным образом. Множество действительных чисел замкнуто относительно введённых четырёх арифметических операций.
Приведём следующую теорему, отражающую важнейшие свойства действительных чисел.
Теорема 3 (совместные свойства рациональных и иррациональных чисел).
1) Сумма, разность, произведение и частное рационального и иррационального чисел есть число иррациональное, за исключением случая, когда нуль (рациональное число) умножается (делится) на иррациональное число и в результате также получается нуль.
2) Между любыми, сколь угодно близкими между собой двумя действительными числами всегда найдётся как рациональное, так и иррациональное число.
3) Чем ближе (на числовой прямой) рациональное число к иррациональному, тем больше цифр в периоде оно имеет. Если представить числовую последовательность, состоящую из рациональных чисел и стремящуюся к иррациональному числу, то количество цифр в периоде у членов этой последовательности стремится к бесконечности.
Сумма (разность) двух иррациональных чисел может быть как иррациональным 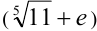 , так и рациональным
, так и рациональным 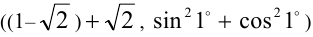 числом. Аналогично произведение (частное) двух иррациональных чисел также может быть как иррациональным
числом. Аналогично произведение (частное) двух иррациональных чисел также может быть как иррациональным 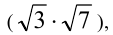 так и рациональным
так и рациональным 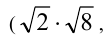
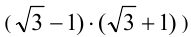 числом. Обратимся к примерам.
числом. Обратимся к примерам.
Пример №91.
Привести примеры нескольких рациональных и иррациональных чисел, расположенных на числовой прямой между 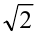 и
и 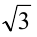 .
.
Решение:
Так как 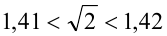 и
и 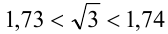 ,то в качестве рациональных чисел, удовлетворяющих условию задачи, можно взять, например, числа
,то в качестве рациональных чисел, удовлетворяющих условию задачи, можно взять, например, числа 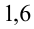 или
или 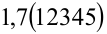 . Примерами иррациональных чисел будут
. Примерами иррациональных чисел будут 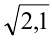 ,
,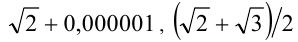 .
.
Пример №92.
Избавиться от иррациональности в знаменателе дроби:
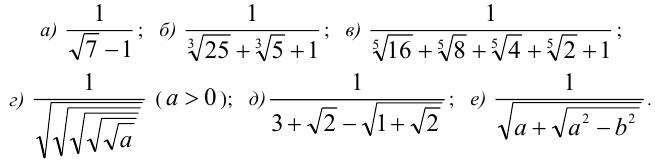
Решение:
Для избавления от иррациональности воспользуемся приёмом одновременного домножения числителя и знаменателя дроби на выражение, сопряжённое к знаменателю (понятие сопряжённого выражения подробно рассматривается ниже в разделе, посвящённом решению иррациональных уравнений и неравенств)
a) 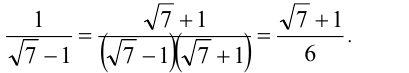
б) Воспользуемся тождеством 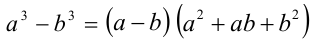 Если положить в нём
Если положить в нём 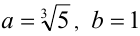 , то получим, что к выражению
, то получим, что к выражению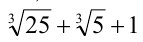 сопряжённым будет
сопряжённым будет 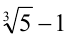 . Далее, домножим одновременно числитель и знаменатель дроби на выражение, сопряжённое к знаменателю:
. Далее, домножим одновременно числитель и знаменатель дроби на выражение, сопряжённое к знаменателю:
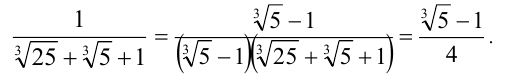
в) Имеем тождество: 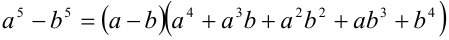 . Если положить в нём
. Если положить в нём 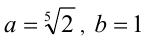 , то получим, что для выражения, находящегося в знаменателе дроби, сопряжённым служит
, то получим, что для выражения, находящегося в знаменателе дроби, сопряжённым служит 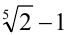 :
:
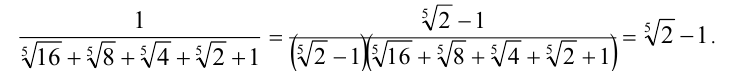
г) Имеем
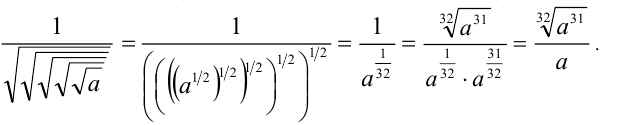
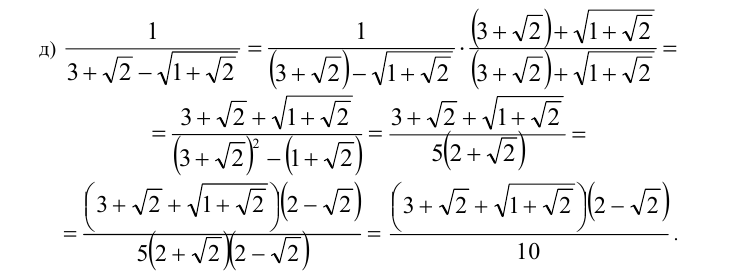
е) При 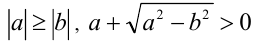 имеем:
имеем: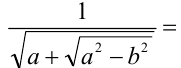
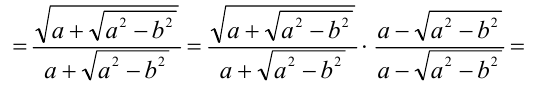
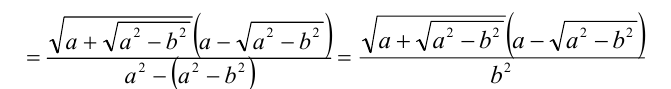
(отметим изменение ОДЗ в процессе преобразований: при умножении и делении на 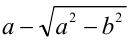 возникло дополнительное ограничение
возникло дополнительное ограничение 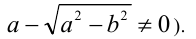
Пример №93.
Упростить числа: 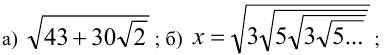
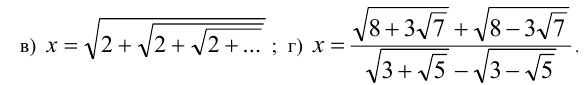
Решение:
а)1-й способ (метод неопределённых коэффициентов). Предположим, что под знаком радикала находится полный квадрат вида
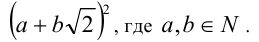
Раскрывая квадрат, получим 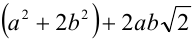 . Равенство
. Равенство
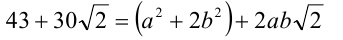
при натуральных а и b выполняется тогда и только тогда, когда 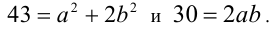 Решим полученную систему подбором. Условию
Решим полученную систему подбором. Условию 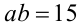 удовлетворяют только четыре пары натуральных чисел
удовлетворяют только четыре пары натуральных чисел
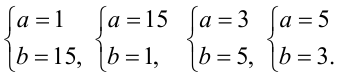
Из них условию 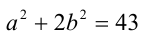 удовлетворяет лишь последняя. Таким образом,
удовлетворяет лишь последняя. Таким образом,
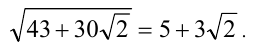
2-й способ (с помощью формулы сложного радикала). Пусть а и b — действительные числа, такие, что 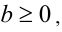
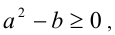
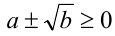 . Тогда справедливо тождество
. Тогда справедливо тождество
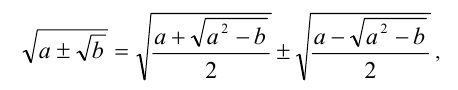
называемое формулой сложного радикала. Доказывается эта формула возведением в квадрат обеих её частей. Эта формула была известна ещё древним арабам. Она позволяет представить один радикал в виде суммы или разности двух других.
Вернёмся к задаче. Имеем 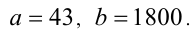 Поэтому
Поэтому 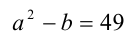 и, следовательно,
и, следовательно, 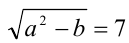 . Применяя формулу сложного радикала, получаем
. Применяя формулу сложного радикала, получаем
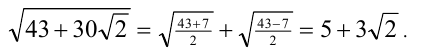
б) 1-й способ. Представим число x в виде
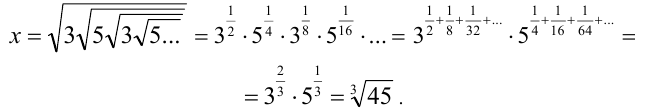
2-й способ. Заметим, что, очевидно, X > 0, и возведем равенство 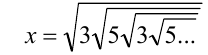 в квадрат последовательно два раза:
в квадрат последовательно два раза:
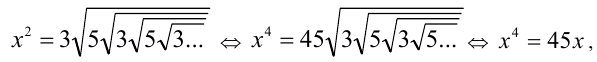
откуда получаем тот же результат.
в) Отметив, что X > 0 , возведём равенство 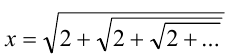 в квадрат:
в квадрат: 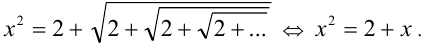 Это квадратное уравнение имеет два корня
Это квадратное уравнение имеет два корня 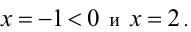 Итак, это число 2.
Итак, это число 2.
г) Отметим, что данное число положительно, и возведём равенство 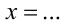 в квадрат. После несложных вычислений получим, что
в квадрат. После несложных вычислений получим, что 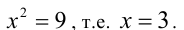
Пример №94.
Сравнить числа 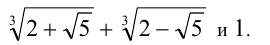
Решение:
Обозначим первое из чисел за x, и возведём равенство
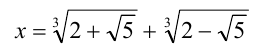
в куб, используя формулу сокращённого умножения
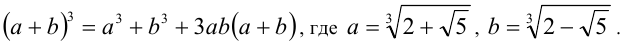
Тогда получим
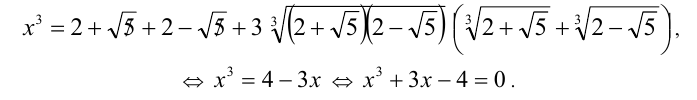
Заметим, что x = 1 является корнем последнего уравнения. Делением многочлена 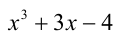 на
на 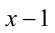 убеждаемся в том, что полученный в результате деления трёхчлен
убеждаемся в том, что полученный в результате деления трёхчлен 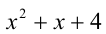 не имеет действительных корней. Таким образом,
не имеет действительных корней. Таким образом, 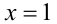 — единственный корень кубического уравнения. Следовательно, первое из сравниваемых равно 1. Ответ: числа равны.
— единственный корень кубического уравнения. Следовательно, первое из сравниваемых равно 1. Ответ: числа равны.
Пример №95.
Что больше: 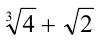 или
или 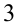 ?
?
Решение:
Уединив кубический корень, возведём оба числа в куб:
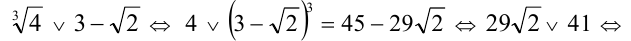
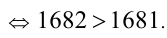
Ответ: первое число больше.
Пример №96.
Что больше: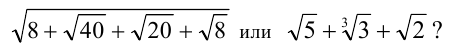
Решение:
Выделяя полный квадрат под знаком квадратного корня в первом из чисел, получим:
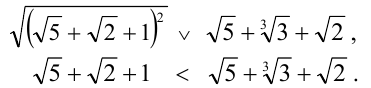
Ответ: второе число больше.
Пример №97.
Расположить в порядке возрастания числа
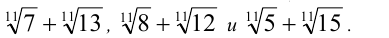
Решение:
Рассмотрим функцию 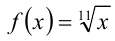 при
при 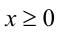 . Введём вспомогательную функцию
. Введём вспомогательную функцию
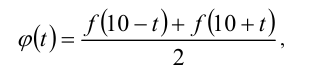
значения которой при 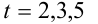 равны соответственно ординатам точек
равны соответственно ординатам точек 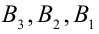 (поскольку отрезки
(поскольку отрезки 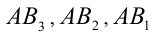 являются соответственно средними линиями трапеций
являются соответственно средними линиями трапеций 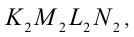
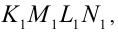
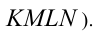 Покажем, что эта функция убывает при
Покажем, что эта функция убывает при 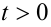 . Действительно, её производная
. Действительно, её производная
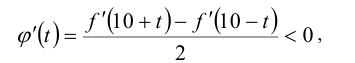
т.к. 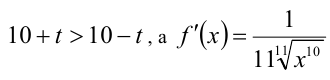 — убывающая функция.
— убывающая функция.
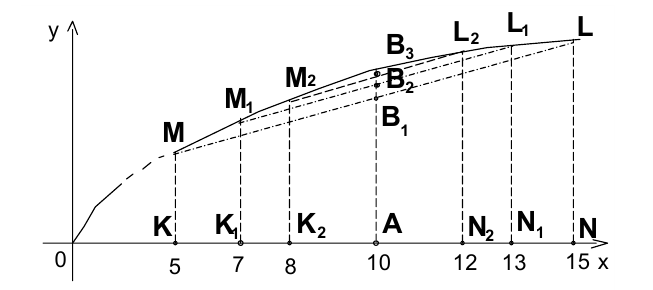
Тогда имеем цепочку неравенств 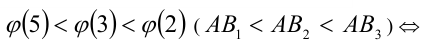
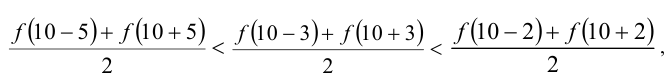
т.е. 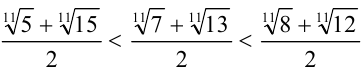 . откуда приходим к ответу.
. откуда приходим к ответу.
Замечание. Полученный результат в действительности является прямым
следствием того, что график функции 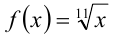 при
при 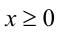 имеет выпуклость, направленную вверх (в строгом смысле).
имеет выпуклость, направленную вверх (в строгом смысле).
Ответ: 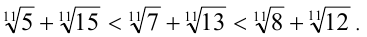
Пример №98.
Найти все целые а и b, для которых один из корней уравнения 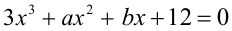 равен
равен 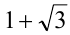
Решение:
Подставим в уравнение вместо 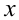 значение корня
значение корня 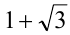 :
:
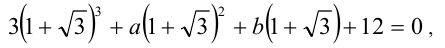
и приведём последнее равенство к виду
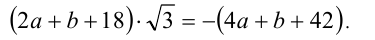
Заметим, что произведение рационального числа 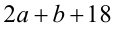 и иррационального числа
и иррационального числа 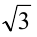 всегда иррационально, за исключением случая, когда
всегда иррационально, за исключением случая, когда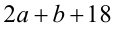 равно нулю (тогда это произведение рационально). В правой части равенства находится рациональное число
равно нулю (тогда это произведение рационально). В правой части равенства находится рациональное число 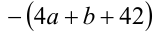 Поэтому равенство возможно
Поэтому равенство возможно
тогда и только тогда, когда 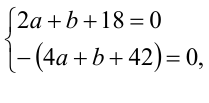
т.е. при 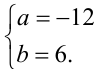
Пример №99.
Найти все целые n, при которых справедливо paвенство
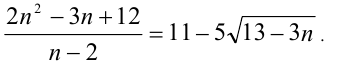
Решение:
Поскольку при целых n число 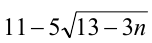 может быть или целым, или иррациональным, а число
может быть или целым, или иррациональным, а число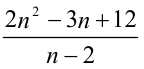 -рационально, то отсюда заключаем, что
-рационально, то отсюда заключаем, что 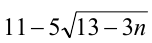 — целое число. Но тогда, в свою очередь, число
— целое число. Но тогда, в свою очередь, число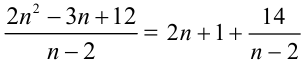 должно принимать целые значения, т.е. дробь
должно принимать целые значения, т.е. дробь 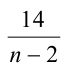 должна быть целым числом. Это возмож-но тогда и только тогда, когда
должна быть целым числом. Это возмож-но тогда и только тогда, когда 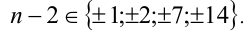 Учтём, что
Учтём, что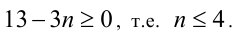 Имеем набор возможных значений n:
Имеем набор возможных значений n:
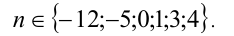
Проверкой убеждаемся, что из всех этих значений исходному равенству удовлетворяет только 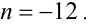
Ответ: 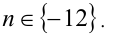
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

