Оглавление:
Сравнение бесконечно малых величин
Пусть 
и 
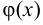— бесконечно малые функции при 
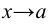. Тогда:
1) если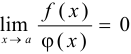 
, то называется бесконечно малой функцией более высокого порядка, чем ;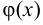
2) если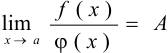 
, 
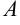
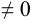, то и 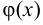называются бесконечно малыми функциями одного порядка;
3) если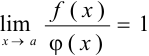 
, то и 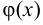называются эквивалентными бесконечно малыми функциями. При этом пишут 
.
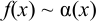При вычислении пределов пользуются следующей теоремой.
Теорема. Предел произведения или частного бесконечно малых функций не изменяется, если любую из них заменить эквивалентной ее бесконечно малой функцией.
Имеют место следующие эквивалентности (при ):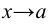
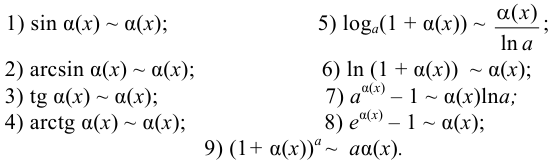
Задача №44.
Используя эквивалентные функции, найти предел
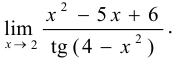
Решение:
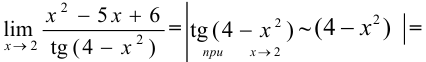
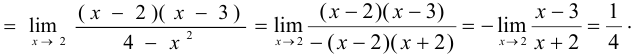
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
| Второй замечательный предел задача с решением |
| Предел с логарифмом задача с решением |
| Непрерывность функции в точке. Классификация точек разрыва |
| Односторонние пределы функций задачи с решением |
