Оглавление:


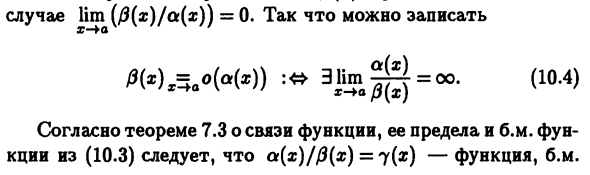

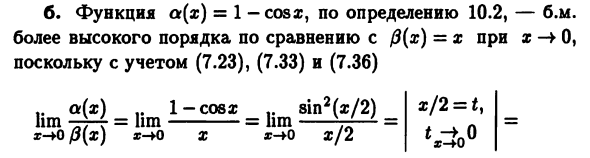

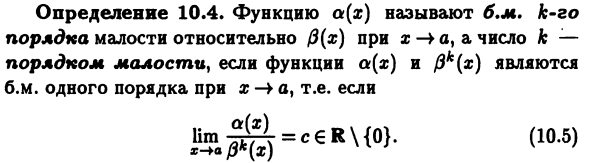




Сравнение бесконечно малых функций
- Основной целевой функцией для сравнения b.m является Сравните природу приближения к нулю, так как x-> a или скорость Желание ноль. Для x-t, функция a (x) и / 3 (x) отличен от нуля в проколотой окрестности о Ноль или неопределенность в точке a, U (a) и точке a. Определение 10.1. Функции a (x) и f3 (x) называются b.m. 1 порядок с x-ba, a (x) x = aO ((3 (x)) (Если присутствует x- * a, символ O гласит «О, большой» Ненулевая конечная оценка отношения a (x) // 3 (x), т.е. X-YU ясно, тогда, согласно (7.24), 3 обода / 3 (x) / a (x) = 1 / с € х ^ а € R \ {0} и запись (3 (x) x = a0 (a (x)) действительны, символ O
► Знаки равенства, содержащие символы Оно, иногда называют Асимптотическая оценка. Определение 10.3. Функции a (x) и @ (x) называются Непревзойденный x-> a, если ни Конечное или бесконечное ограничение их отношений, т.е. $ lim a (x) // 3 (x) (и $ lim fi (x) / a (x)). Пример 10.1 а. Функция a (x) = x и / J (x) = sin2x Определение 10.1-B.M.x -4 0 первого порядка Рассмотрим (7.24), (7.33) и (7.36) гм -N- (Х) хорошо стоит? -Fo l1. Sint . = 21im = 2 ^ 0. Я 6.
Переходные характеристики, то есть a (x) x = a0 (/ 3 (x)) А / 3 (aOx a Это означает справедливость описания теоремы Людмила Фирмаль
По определению функция a (x) = 1-косар, м.м. / 3 (x) = x как x-> выше 0, Потому что (7.23), (7.33) и (7.36) w / 2 = *, «V», y 1-cosa? .. sin2 (a? / 2) hm -T7 ~ = hm = hm v » = x- ¥ Qp [X) x-YO X x- + 0 X / 2 = lim lim sin t = 1 • 0 = 0. t-i) t * -u с. Функция a (x) =% fx равна b.m. подчиненный (По сравнению с 3 (x) = x при x-> 0, X д. Функции a (x) = xsin (l / x) и ^ (x) = x Определение 10.3-Непревзойденный b.m.x-0, из-за ограничений .. а (х) а; грех (л / о :). 1 lim-rm-t = urn i-s — i = hm sin- 0 () X Не существует (ни конечной, ни бесконечной ссылки Пример 7.5). е.
Степенная функция xn с показателем степени n € N n> 1 — это то же самое, что и x-> a.m. Высший порядок lim (xn / xn ~ 1) = так по сравнению с x11 «1, то есть ^^^ (x» «1) = limx = 0. »0 Более точное сравнение при необходимости Действует как элемент действия x->, один из которых выбран Это называется основным как своего рода стандарт. Конечно, выбор основного БМ в некоторой степени произвольный (Они попытаются выбрать более простой вариант: x, если x- x 0; x-1, если x-> 1; 1 / x х-хсо и т. д.) 0k (x) градусов основной базы. функция P (x) с различными показателями k> 0 (если k <0, Pk (x) бм) Создать шкалу сравнения, чтобы оценить больше Комплексная функция b.m a (x). Определение 10.4.
- Функция a (x) называется b.m. к-й x-> 0 (x) как a и число A в малом порядке- Функции a (x) и f3k (x) Тот же порядок, что и во второй половине дня x-> a, т.е. слово «маленький» в этом случае обычно опускается. Примечание: 1) Заказать конкретную функцию до 1 бм Это может быть любое положительное число. 2) Когда порядок функции Порядок функций (5 (x) равен 1 / & для a (x); 3) Функция a (x) не всегда для bm} Все степени Pk (x) могут указывать на различный порядок k. Пример 10.2 а. Согласно функции ot (x) = 1-cos i Определение 10.4, б.м. порядок k = 2 для f3 (x) = x Учитывать x- + 0, (7.23), (7.33) и (7.36) ободок х- * 0 a (x) 1-cosa_3sin2 (a / 2) = Оправа = Оправа ar- + O 1 .. sin2 * 1 ,. Синт .. Синф = -hm — = — = — lim lim 2 t2 2t- ¥ 0 t t- + o t б. Рассмотрим функцию a (x) = a1 / 1, a € (0, 1) и fl (x) -x) PM x-) • +0. Когда fc> 0 Lim ^ C- * — «+ 0 X * (10.6) конечно ободок 1 / х = т, = lim a * £ * = lim = 0 Согласно (7.32).
# Функции, связанные с определением порядка одного бм Другое не всегда легко. Я могу рекомендовать этот заказ Действие: 1) Запишите отношение a (x) // Zk (x) под знаком предела. 2) Проанализируйте записанное отношение и попробуйте Упростите это. 3) Предложения, основанные на известных результатах Предполагая, что возможные значения k1 существуют Существует ненулевой конечный предел. 4) Рассчитать пределы и проверить допущения. Пример 10.3. Определить порядок m. функция tgx -inxx найти такое число k> 0 как x- * 0 для x,
Следовательно, м. x-> H-0 действует как allx Эквивалентно xk, если k> 0, но указывает на эту функцию Порядок малости по x не выполняется. Людмила Фирмаль
Вот так .. тгж-синж = A € R \ {0}. (10.7) as — ru l » У нас есть .. тгж-сипж, (l-cosg) грех и .. 2sin2 (w / 2) «грех hm-r = hm r— = hm \ r ~ ‘• х- * 0ХКх- + 0 † * COS † х- ¥ 0 † * COS † На этом этапе для i-fO, согласно (7.35) и (7.36) (Btj) / f- \ 1 и ccr- \ 1, а также (7.23) и (7.33) Определяет, что условие (10.7) выполняется при k = 3. На самом деле, предел расчета непосредственно при k = 3 Дайте значение A = 1/2: .. тгж-синж .. 2вш2 (ж / 2) sinx hm- = = hm): ‘= 4 (w / 2) 2 w cos w 1 грех (w / 2) грех (w / 2) грех w..11 = -hm-〜 ^ — • хм — ^ — r-1 • хм хм = — 2x-fO x / 2 x- * o x / 2 z- * o x x- ^ Если k> 3, получается бесконечный предел, Если 0 <k <3, предел равен нулю.
Смотрите также:
| Непрерывность основных элементарных функций | Эквивалентные бесконечно малые функции |
| О вычислении нуля функции, непрерывной на отрезке | Главная часть бесконечно малой функции |

