Оглавление:
Прямые — самые простые линии на плоскости. Им соответствуют и самые простые уравнения — уравнения первой степени.
Прямую на плоскости можно задать несколькими способами:
Задание прямой с помощью точки и направляющего вектора.
Направляющим вектором прямой 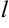 называется всякий ненулевой вектор
называется всякий ненулевой вектор 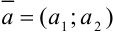 , параллельный этой прямой.
, параллельный этой прямой.
Любая прямая имеет бесконечное множество направляющих векторов, коллинеарных между собой.
Пусть задана точка 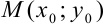 , через которую проходит прямая
, через которую проходит прямая 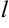 , и её направляющий вектор
, и её направляющий вектор 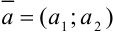 (рис. 6.1).
(рис. 6.1).
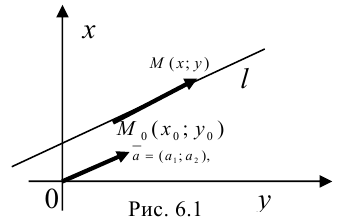
- Выберем произвольную
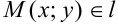 .
. - Найдем координаты вектора
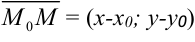 .
. - Запишем направляющий вектор
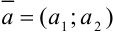 .
. - Воспользуемся условием коллинеарности векторов
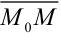 и
и  ; их одноименные координаты должны быть пропорциональны. Поэтому уравнение прямой имеет вид:
; их одноименные координаты должны быть пропорциональны. Поэтому уравнение прямой имеет вид:
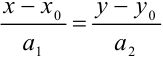 (1) — уравнение прямой, проходящей через точку
(1) — уравнение прямой, проходящей через точку 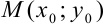 с направляющим вектором
с направляющим вектором 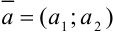 .
.
Пример №6.2.
Составьте уравнение прямой, проходящей через точку 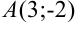 и имеющей направляющий вектор
и имеющей направляющий вектор 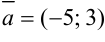 .
.
Решение:
Подставим координаты точки и направляющего вектора в уравнение (1): 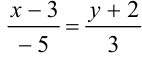 .
.
Задание прямой через две точки.
Пусть заданы две точки 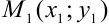 и
и 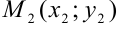 . Через них можно провести прямую, и притом только одну. Составим уравнение прямой, проходящей через точки
. Через них можно провести прямую, и притом только одну. Составим уравнение прямой, проходящей через точки 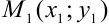 и
и 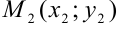 .
.
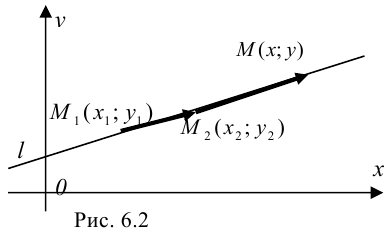
Для этого (рис. 6.2):
- Выберем на прямой
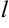 точку
точку 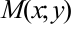 .
. - Найдем координаты вектора
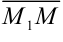 :
: 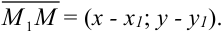
- Найдем координаты направляющего вектора
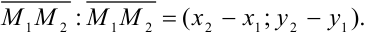
- Векторы
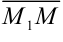 и
и 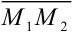 коллинеарны, так как лежат на одной прямой; следовательно, их координаты пропорциональны.
коллинеарны, так как лежат на одной прямой; следовательно, их координаты пропорциональны.
Искомое уравнение прямой имеет вид: 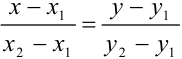 (2) — уравнение прямой, проходящей через точки
(2) — уравнение прямой, проходящей через точки 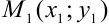 и
и 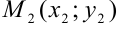 .
.
Пример №6.3.
Составьте уравнение прямой, проходящей через точки 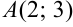 и
и 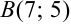 .
.
Решение:
Подставив в формулу (2) координаты данных точек, получим искомое уравнение прямой: 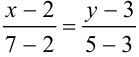 .
.
Ответ: 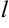 :
: 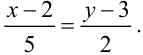
Задание прямой, проходящей через точку с заданным нормальным вектором.
Нормальным вектором прямой 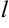 называется любой ненулевой вектор
называется любой ненулевой вектор 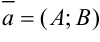 , перпендикулярный этой прямой.
, перпендикулярный этой прямой.
Пусть заданы точка 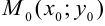 и нормальный вектор
и нормальный вектор 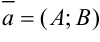 (рис.6.3).
(рис.6.3).
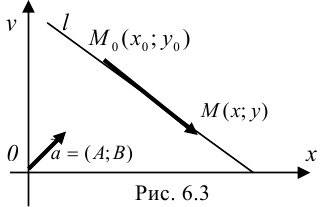
Для составления уравнения прямой, проходящей через точку 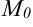 и имеющей нормальный вектор
и имеющей нормальный вектор  :
:
- Выберем на прямой
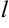 произвольную точку
произвольную точку 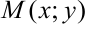 .
. - Найдем координаты вектора
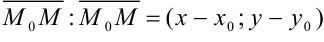 .
. - Запишем координаты заданного нормального вектора
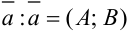 .
. - Воспользуемся условием перпендикулярности векторов
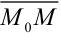 и
и  ; их скалярное произведение равно нулю, т.е.
; их скалярное произведение равно нулю, т.е. 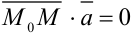 .
.
Так как скалярное произведение векторов, заданных своими координатами, равно сумме произведений одноименных координат, то уравнение прямой  примет вид:
примет вид:
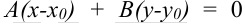 (3) — уравнение прямой, проходящей через точку
(3) — уравнение прямой, проходящей через точку 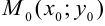 с заданным нормальным вектором
с заданным нормальным вектором 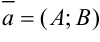 .
.
Пример №6.4.
Составьте уравнение прямой, проходящей через точку 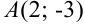 перпендикулярно вектору
перпендикулярно вектору 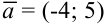 .
.
Решение:
Вектор  будет являться нормальным вектором данной прямой. Подставим в формулу (3) координаты точки
будет являться нормальным вектором данной прямой. Подставим в формулу (3) координаты точки  и вектора
и вектора  , получим искомое уравнение прямой:
, получим искомое уравнение прямой:
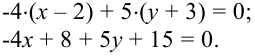
Ответ: 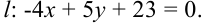
Задание прямой, проходящей через точку с заданным угловым коэффициентом.
Пусть заданы точка 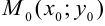 и нормальный вектор
и нормальный вектор 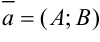 . Тогда уравнение прямой, проходящей через точку с заданным нормальным вектором будет иметь вид:
. Тогда уравнение прямой, проходящей через точку с заданным нормальным вектором будет иметь вид:
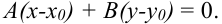
Разделим каждое слагаемое на 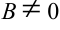 .
.
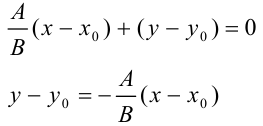
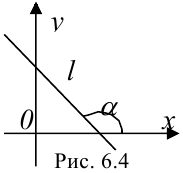
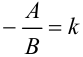 , где
, где 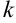 — угловой коэффициент прямой, равный тангенсу угла наклона
— угловой коэффициент прямой, равный тангенсу угла наклона 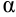 , образованной прямой с положительным направлением оси
, образованной прямой с положительным направлением оси 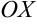 (рис. 6.4):
(рис. 6.4):
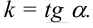
Тогда 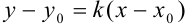 (4) — уравнение прямой, проходящей через точку
(4) — уравнение прямой, проходящей через точку 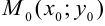 с данным угловым коэффициентом
с данным угловым коэффициентом 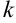 .
.
Пример №6.5.
Составьте уравнение прямой, проходящей через точку 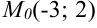 и образующей с положительным направлением оси
и образующей с положительным направлением оси 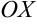 угол
угол 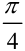 .
.
Решение:
Найдём угловой коэффициент прямой: 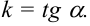
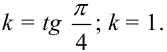
Подставим 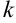 и координаты точки
и координаты точки 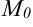 в уравнение (4):
в уравнение (4):
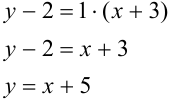
Ответ: 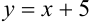
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Операции над векторами в координатах. |
| Уравнение линии на плоскости. |
| Виды уравнений прямой. |
| Угол между двумя прямыми. |

