Оглавление:
Способы задания движения точки
Естественный способ
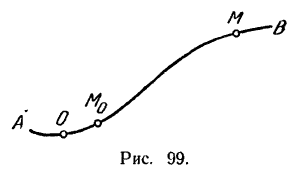
Предположим, что точка совершает движение по некоторой траектории 
(рис. 99). Возьмем на этой траектории какую-либо произвольную (неподвижную) точку 
и назовем ее началом отсчета расстояний. Измеренная в линейных единицах длина дуги 
называется расстоянием точки 
от начала отсчета или ее дуговой координатой. Это расстояние мы будем обозначать
строчной буквой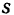 
(в отличие от пути, пройденного точкой, обозначаемого прописной буквой 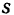). Для определенности нужно условиться о направлении отсчета дуговой координаты s и считать величину s положительной, если расстояние откладывается по траектории в одну какую-либо сторону от начала отсчета 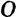, и отрицательной, если оно откладывается в противоположную сторону. Выбор положительного направления отсчета, вообще говоря, произволен.
Еще раз подчеркнем, что расстояние s точки от начала отсчета нельзя смешивать с длиной пути 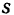, пройденного точкой за соответствующий промежуток времени.
Пусть, например, некоторая точка за промежуток времени от 0 до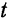 
переместилась по своей траектории из начала отсчета 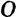в положение 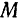(рис. 99) и обратно. Тогда в момент времени 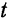расстояние точки от начала отсчета 
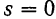. Путь же, пройденный точкой за промежуток времени 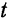, равен удвоенной дуге 
.
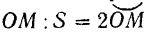В каждый момент точка может занимать только одно определенное положение на траектории, и следовательно, ее расстояние 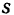от начала отсчета есть некоторая однозначная функция времени 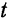Зависимость между переменным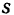и и 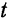может быть выражена уравнением
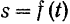
Уравнение 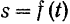называется уравнением движения точки по траектории.
Траектория точки может быть задана различными способами: пли аналитически, т. е. в виде уравнения кривой, или геометрически. Представляющая собой закон движения точки по траектории функция 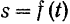точно так же может быть задана или аналитически или в виде графика. График функции 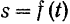называется графиком движения.
График движения нельзя отождествлять с траекторией движения точки.
Так, например, при равномерном движении точки 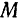по некоторой кривой 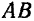(рис. 99) траекторией движения точки будет эта кривая. Графиком же движения точки (графиком функции 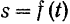) будет прямая линия,так как при равномерном движении точки приращение ее расстояния 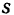от начала отсчета прямо пропорционально приращению времени t ее движения.
Рассмотренный способ определения положения точки называется естественным. Таким образом, при естественном способе задания движения точки должны быть известны: а) траектория точки в выбранной системе отсчета, б) начало и положительное направление отсчета, в) закон движения точки по данной траектории: .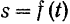
Координатный способ
Координатный способ задания движения точки основан на том, что положение точки относительно некоторой системы отсчета всегда может быть определено при помощи некоторой совокупности чисел, называемых ее координатами.
Системы координат могут быть различными. Мы остановимся только на способе задания движения точки в прямоугольной (декартовой) системе координат.
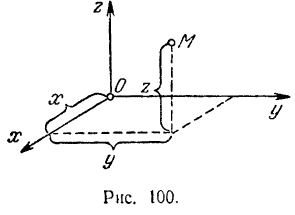
Положение точки 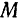относительно этой системы координат вполне определяется тремя координатами точк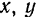и 
и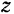 
(рис. 100). При движении точки ее координаты изменяются с течением времени, т. е. будут являться некоторыми функциями аргумента :
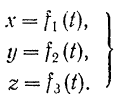
Уравнения (51) называются уравнениями движения точка в декартовых координатах.
Если нам будет известно, как изменяются со временем координаты точки, совершающей некоторое движение, т.е. если нам будут известны уравнения (51), то мы всегда сможем определить координаты этой точки для любого момента времени, а следовательно, определить и ее положение относительно данной системы отсчета.
Сели во все время движения О точка остается в одной плоскости, то, расположив систему двух взаимно перпендикулярных осей х и у в этой плоскости (рис. 101), мы получим возможность определять любое положение точки в данной плоскости только двумя ее координатами. Следовательно, плоское движение точки определяется двумя уравнениями движения в прямоугольных координатах:
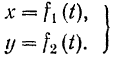
Если точка совершает прямолинейное движение, то можно принять прямую, по которой движется точка, за одну из координатных осей, например, за ось 
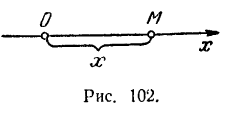
. Положение точки на этой оси вполне определяется одной координатой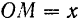 
(рис. 102), и следовательно, прямолинейное движение точки задается одним уравнением:
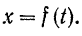
Уравнения движения точки с прямоугольных координатах (51) и (52), задавая положение движущейся точки в любой момент времени, определяют тем самым и ее траекторию. Исключая время t из заданных уравнений движения точки, мы получаем уравнение ее траектории.
Векторный способ
Положение движущейся точки 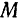(рис. 103) относительно какой-либо системы отсчета однозначно определяется в любой момент времени вектором 
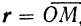, проведенным из какой-либо точки 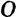, неподвижной относительно выбранной системы отсчета. Этот вектор называется радиусом-вектором топки .
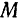При движении точки 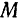ее радиус-вектор непрерывно изменяется (в общем случае и по модулю и по направлению), т.е. является векторной функцией времени
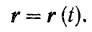
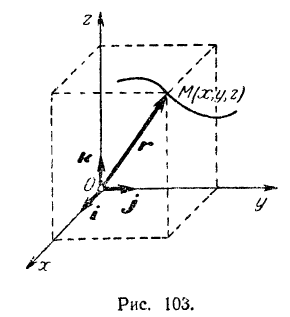
Уравнение (54) называется векторным уравнением движения точки.
Если принять точку за начало прямоугольной системы координат и разложить радиус-вектор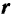 
по осям координат, то для радиуса-вектора, определяющего положение точки 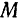(рис. 103), можно написать следующее выражение
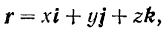
где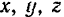 
— проекции радиуса-вектора на координатные оси, равные координатам движущейся точки 
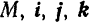— орты координатных осей .
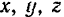Зная, как изменяются координаты движущейся точки 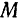, т.е. зная уравнения (51) ее движения в декартовых координатах, можно для любого момента времени построить и радиус-вектор точки.
Таким образом, задание одного векторного уравнения (54) равносильно заданию трех скалярных уравнений (51). Вследствие этого векторный способ определения движения точки оказывается весьма удобным для доказательства теорем и установления общих зависимостей.
При решении же конкретных задач, когда требуется получить определенный численный результат, чаще более удобными оказываются естественный или координатный способы задания движения точки.
В большинстве практических задач движение точки определяется заданными условиями, в частности, заданной конструкцией механизма.
По этим условиям и находятся, аналитически или графически, траектория и уравнения движения интересующей точки.
Пример задачи:
Кривошип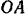 
(рис. 104) равномерно вращается вокруг неподвижной оси 
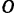и приводит в движение ползун 
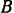при помощи шатуна 
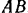, соединенного шарнирно с кривошипом и ползуном. Угол 
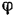поворота кривошипа изменяется со временем по закону 
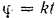. Определить в прямоугольных координатах уравнения
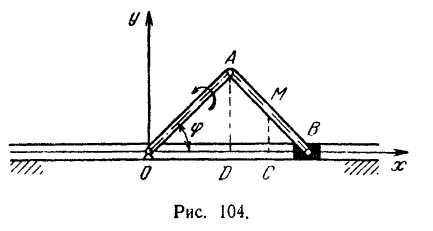
движения средней точки 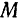шатуна и найти траекторию этой точки. Длина кривошипа 
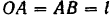. (Неподвижная направляющая ползуна расположена позади кривошипно-шатунного механизма.)
Решение:
Проведем прямоугольные координатные ос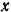и 
и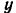 
так, как показано на рис. 104. Треугольник 
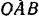— равнобедренный, следовательно, 
.
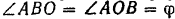Координатами точки 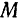в данной системе координат будут:
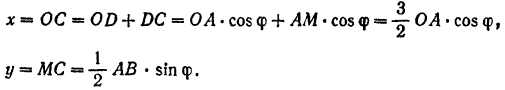
Подставляя в эти уравнения значения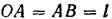 
и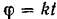 
получаем искомые уравнения движения средней точки 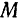шатуна:
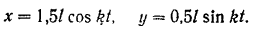
Чтобы найти траекторию точки 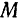, исключим время 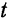из ее уравнений движения. Для этого найдем из данных уравнений значения
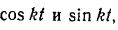
возведем их в квадрат и сложим:
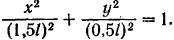
Таким образом, траекторией средней точки шатуна будет кривая, определяемая последним уравнением. Кривая эта есть эллипс с центром в неподвижной точке и с полуосями
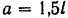
и
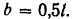
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
