Оглавление:
Способ последовательного дифференцирования
Решение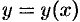 
уравнения (65.2) ищем в виде ряда Тейлора:
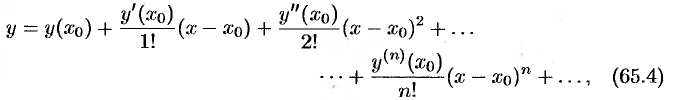
при этом первые два коэффициента находим из начальных условий (65.3). Подставив в уравнение (65.2) значения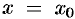 
, 
, 
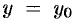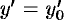, находим третий коэффициент: 
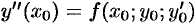. Значения 
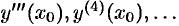находим путем последовательного дифференцирования уравнения (65.2) по 
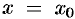и вычисления производных при . Найденные значения производных (коэффициентов) подставляем в равенство (65.4). Ряд (65.4) представляет искомое частное решение уравнения (65.2) для тех значений , при которых он сходится. Частичная сумма этого ряда будет приближенным решением дифференциального уравнения (65.2).
Рассмотренный способ применим и для построения общего решения уравнения (65.2), есл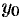и 
и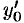 
рассматривать как произвольные постоянные.
Способ последовательного дифференцирования применим для решения дифференциальных уравнений любого порядка.
Пример №65.4.
Методом последовательного дифференцирования найти пять первых членов (отличных от нуля) разложения в ряд решения уравнения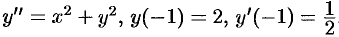 
.
Решение:
Будем искать решение уравнения в виде
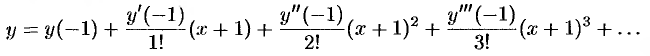
Здесь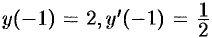 
. Находим 
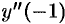, подставив 
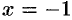в исходное уравнение: 
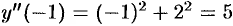. Для нахождения последующих коэффициентов дифференцируем заданное дифференциальное! уравнение:
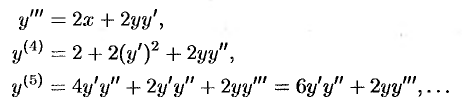
При 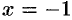имеем:
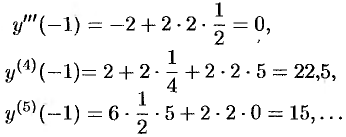
Подставляя найденные значения производных в искомый ряд, получим:
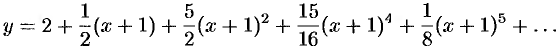
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Приближенное вычисление определенных интегралов |
| Приближенное решение дифференциальных уравнений |
| Способ неопределенных коэффициентов |
| Тригонометрический ряд Фурье |
