Оглавление:
Способ неопределенных коэффициентов
Этот способ приближенного решения наиболее удобен для интегрирования линейных дифференциальных уравнений с переменными коэффициентами.
Пусть, например, требуется решить уравнение
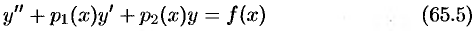
с начальными условиями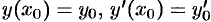 
.
Предполагая, что коэффициенты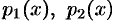 
и свободный член 
разлагаются в ряды по степеням 
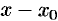, сходящиеся в некотором интервале 
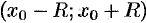, искомое решение 
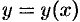ищем в виде степенного ряда
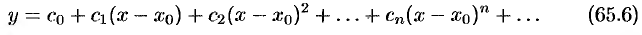
с неопределенными коэффициентами.
Коэффициенты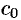 
и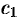 
определяются при помощи начальных условий 
.
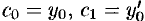Для нахождения последующих коэффициентов дифференцируем ряд (65.6) два раза (каков порядок уравнения) и подставляем выражения для функции 
и ее производных в уравнение (65.5), заменив в нем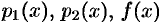 
их разложениями. В результате получаем тождество, из которого методом неопределенных коэффициентов находим недостающие коэффициенты. Построенный ряд (65.6) сходится в том же интервале 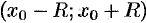и служит решением уравнения (65.5).
Пример №65.5.
Найти решение уравнения
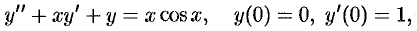
используя метод неопределенных коэффициентов.
Решение:
Разложим коэффициенты уравнения в степенные ряды:
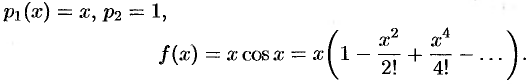
Ищем решение уравнения в виде ряда
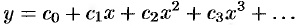
Тогда
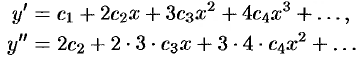
Из начальных условий находим: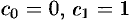 
. Подставляем полученные ряды в дифференциальное уравнение:
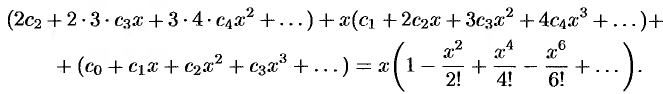
Приравниваем коэффициенты при одинаковых степенях 
:
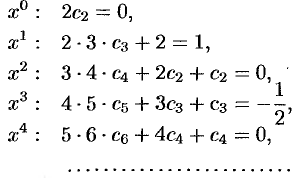
Отсюда находим, что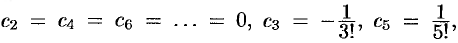 
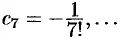Таким образом, получаем решение уравнения в виде
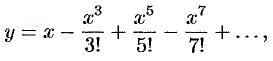
т. е.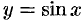 
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Приближенное решение дифференциальных уравнений |
| Способ последовательного дифференцирования |
| Тригонометрический ряд Фурье |
| Разложение в ряд Фурье четных и нечетных функций |
