Оглавление:













Специальные задачи динамики. Удар
- Шок-это процесс, в котором очень большая сила действует в течение очень короткого времени. Взаимный ток времени часто равен 1000 минутам 1 секунде, и даже 1 тысяче минут 1 секунде. Величина силы, оказываемой на тело при ударе, может быть в несколько тысяч раз больше или в десятки тысяч раз больше веса тела. В теорию влияния классической механики вводится следующая идеализация этого процесса-предельный переход к бесконечно большой силе с конечным импульсом s, действующей в бесконечно короткое время мгновенная сила. Силы f во времени t, в результате времени t для начала его действия.
После этого ее порыв проходит вот так 5 ФДТ- Определить приведенный выше импульс удара s, соответственно, m-0, то есть Здесь предполагается, что бесконечно большая мгновенная сила действует в течение бесконечно короткого промежутка времени. Величина ударного импульса s считается конечной. Применим теорему к изменению импульса при ударе Под действием мгновенной силы движение точки силы равно нулю, а скорость точки изменяется поэтапно. На самом деле скачок скорости происходит за короткое время. Осевая линия-это ось, проходящая через центр тяжести сталкивающегося тела.
Материальной точкой называется материальное тело, праща-тельными движениями которого, по сравнению с поступательными, можно пренебречь. Людмила Фирмаль
Если точка соприкосновения сталкивающегося объекта находится на линии, то удар называется троллем Центр c c касательная плоскость, проведенная в точке соприкосновения с поверхностью переход к схеме лютпо твердого тела и деформируемого тела. В зависимости от степени восстановления в недеформируемом состоянии удар подразделяют на неупругий, частично упругий и упругий. Если установлено недеформируемое состояние ударного тела r, то удар называется упругим.
Движется ли он таким же образом с центром тяжести удара Скорость. Если несформированное положение не восстанавливается полностью, то воздействие называется частичным elasticity. At в конце удара центр объекта перемещается с разной скоростью. Воздействие называется упругостью, и восстановление восстанавливается. Если не деформируется Прямой центр 2 объектов для учета неупругого воздействия введем следующие обозначения На первом этапе происходит деформация сталкивающегося тела. Этап 2-частичное восстановление неповрежденного state. At в конце этапа 1 и в начале этапа 2 скорость центра тяжести объекта равна скорости окончания соответствующего неупругого удара.
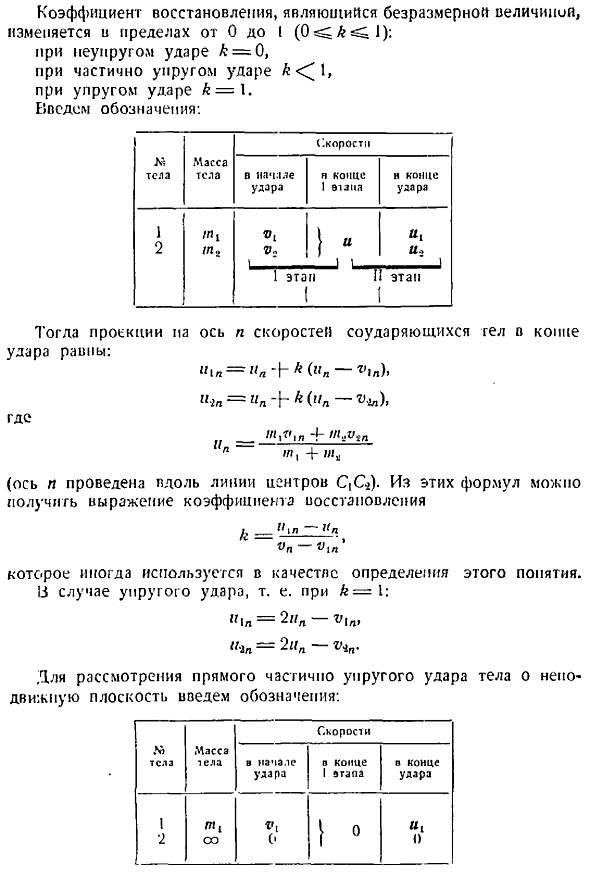
В конце второго этапа центр тяжести объекта уже имеет другую скорость, а коэффициент восстановления n деформации На минуту. Вторая сила Вводя определение этой мгновенной силы, мы возвращаемся к теории влияния классической механики. Кин. Это безразмерная величина. Он изменяется от 0 до i oigft l неупругое воздействие, k 0, частичное упругое воздействие, a 1, упругое воздействие, b 1 Вводится следующая нотация. Оси l от скорости сталкивающихся объектов Затем проекция па Ш —. L — i t.
Нарисуйте вдоль оси и центральной линии c c4. Из этих формул можно получить формулу для коэффициента восстановления к Это понятие иногда используется в качестве definition. In случай упругого удара, то есть с fe 1 Для учета прямого частичного упругого удара В движущейся плоскости, введем обозначение. А проекция-это высота свободы Скорость центра тяжести падающего тела равна оси l n — ai, а a 1 — l, где происходит падение объекта на неподвижную плоскость. — Отражательная высота ударного тела рис. 166. Когда рассматривать После частичной эластичности Диагональный Центр Никогда. 2 упругих тел Рассматриваются сталкивающиеся тела Рисунок 167. 166. Гладкий.
Ось n-это нарисованные вдоль центральной линии c, Сиджей рис. 167. Ось Т перпендикулярна оси р, а проекция скорости центра тяжести коллайдера в начале столкновения равна М 1 0 потому что, потому что М. М Сина, ОИ, , о, Сина. Проекция скорости центра тяжести сталкивающегося тела в ударной копии рис. 168 — Так и есть Модуль скорости удара. — — 1. Сталкивающиеся тела копий При изучении косого частичного упругого воздействия объектов на неподвижные и неподвижные поверхности поверхности тела они считаются идеально гладкими. Направление оси Лита показано на рисунке. 169.
Проекция скорости центра тяжести падающего тела в начале удара принимает следующий вид Проекции скорости центра тяжести падающего тела в конце удара, уравнение -это очень важно, — сказал он. И n — t, есть. Коэффициент скорости центра тяжести падающего тела в конце удара определяется по формуле Коэффициент восстановления рассчитывается по формуле a. Где x-угол падения, — угол отражения. Рис. 16Р.
В конце столкновения скорость сталкивающегося объекта вычисляется по формуле в конце проекции ts1a, ui, ult, ujt 1Я Я —. — Ци 5 Определите скорость обоих тел в конце Лар. Модуль скорости эквивалентен и — и 7. Bj Направление скорости определяется по формуле. — Джи Ы тг. Неподвижная плоскость имеет очень большую массу и должна иметь скорость 0 до столкновения. Рассчитайте прямую атаку про-429 из 2 агентств. Шаррв и неподвижен.
- Скорость ТТ, которая является центром тяжести первого шара Общая скорость Ноль. Отправьте влево вдоль крыши c c4. Проекция скорости центра тяжести шара на ось n в начале удара образует Проекция полной скорости удара Поздняя неэластичность Найти искомую скорость ti проекции центр тяжести первого шара и начало неупругого удара Р р подбородок oularnogs навстречу друг другу 20 6-20-0. ———— 18 м с. Задача 430. Скорость Центра o, 6 л, сек, t 2 10 л ССК. Вес hep-g. Определите шар, несущий 2-й шар, и если после неупругого удара шар остается Решение.
Укажите ось n вдоль центральной линии c c2. Проекция скорости центра тяжести шара на ось n в начале удара выглядит так bi 6 м с, а n −10 м с. По условию pe потому, что проекция на ось полной скорости после упругого удара равна нулю Я я — з 1Н 0 Окуда Пт — — я 6 кг. Размер ударного импульса выглядит следующим образом ы М7 е- я е 10 60 Проблема 431. Определите скорость центра тяжести 2-х шаров. Rt 12 кг и p, 10 кг 2 шарика соответственно в конце частичного упругого удара, если скорость в начале удара была равна м с Направление. Коэффициент восстановления г при ударе равен 0, 8. Р Е В Е и Е. Точка оси n вдоль осевой линии ctc в направлении движения Мяч. Задача прогнозирования скорости до 431.
Всякое механическое движение материальных тел происходит с течением времени в пространстве. Людмила Фирмаль
Равные по оси l центра тяжести шара в начале удара nln 10 м с, ti2 6 м с. Проекция полной скорости на ось р в случае неупругого удара Проекция требуемой скорости центра тяжести шара в момент окончания упругого удара задается формулой Я н — 8. 18- −0. 8 8. 18-10 6. 72 м с И. М ООН К ун-0, н 8. 18 0. 8 8. 18-6 9. 92 м с. Канава справа. Проекция скорости на ось n центра тяжести шара в начале удара составит r n 10 м с, vin — b м с. Проекция полной скорости на ось l в случае неупругого удара Определяется проекция требуемой скорости в конце упругого удара И Л К К а — 2, 73- −0. 8 2, 73-10 −3, 07 м с, НИА а А — ВТЭ 2. 73 −0. 8 2. 73 Джей-6 9, 65 м с.
Символ u1ya uin указывает на то, что после lar шар будет двигаться в разных направлениях. То есть первый шар-это олененок, а второй-справа. Задача 433. После частично упругого удара шар достигает высоты l 81 см. Коэффициент восстановления равен 0, 9. Решение. Ось n расположена вертикально вниз. Скорость центра тяжести шара в начале удара, скорость неподвижной плоскости равна нулю ОС 0. Его масса m бесконечно велика, то есть m4 oe. Полная скорость и проекция на n-осевой неупругий случай Последствия равны Проекция скорости центра тяжести шара на ось l в конце удара будет равна nin n k iin-vln. ООН 0, Итак Иш — Знак минус указывает на то, что скорость мяча в конце удара направлена вверх.
Зависимость между модулем скорости центра тяжести шара в начале и конце удара равна О Мяч выпал на свободу. 2 После частично упругого удара мяч начинает подниматься В случае неупругого удара, мяч не отскакивает от плоскости. То есть, Л 0. Из выражения i получаем Л 0. В случае упругого удара мяч должен отскочить в исходное положение. То есть из уравнения bs bv 5, Л 1. Частично упругое воздействие 9 a, и поэтому 0 k 1, когда деревянный шар ударяется о сталь, a 0, 55, шар из слоновой кости ударяется о пластину из того же материала, k 0, 90, когда стеклянный шар ударяется о стеклянную пластину, k 0, 94 и g. Проблема 434.
В момент столкновения 2 одинаковых поступательно движущихся шаров скорость центра тяжести левого шара была направлена вправо вдоль осевой линии, а скорость центра тяжести правого шара 2 была перпендикулярна осевой линии. Учитывая упругость удара, определите скорость центра тяжести шара в конце удара. Решение. Направьте ось l вдоль осевой линии ctci, а ось m-перпендикулярно. Вычислите проекцию скорости n i. Проекция полной скорости шара на ось lar рассчитывается по формуле Неупругий корпус Когда это происходит, поэтому Мяч, то wx t, то t Я Центральная скорость Теперь определим модуль конца удара по формуле Г в УА, у ух.
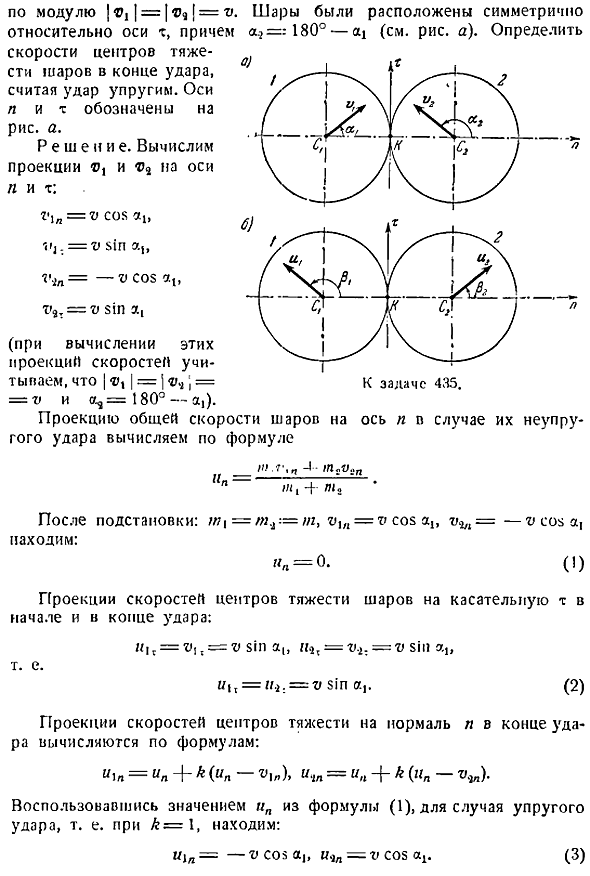
Используя формулы 2 и 3, получаем и, 0, и, 3 То есть после упругого удара шар слева остается неподвижным. Направление скорости определяется с помощью угла b см. Рисунок b. Задача 435. Самое интенсивное столкновение из 2 одинаковых действий- Движущийся шар центра тяжести со скоростью nx равен По модулю oh о ок. Шар был расположен симметрично оси с при q 180 — a см. Рисунок a. Учитывая упругость удара, определите скорость центра тяжести шара в конце удара. С меткой освещения вала Рисунок a. Проекция сетки Проекция скорости центра тяжести Касательная Т 180 —а.
Прогноз суммарной скорости мяча при его попадании рассчитывается по формуле Неупругий После замены Проекция скорости центроида ra вычисляется по формуле, — Т Вт. Используя значение Формулы 1 и для упругого удара, то есть для 1 1л 3 Модуль скорости центра тяжести снаряда в конце удара рассчитывается по формуле Я х ч l1n, У У Э- Используя формулы 2 и 3, получаем Направление этих скоростей определяется с помощью угла p, pa см. Рисунок b. Таким образом, рассматриваемый косой удар не изменяет коэффициента скорости центра тяжести шара, а угол, под которым формируется вектор скорости с осью n, изменяет положение. Задача 436. Свободный падающий шар попадает в неподвижный шар.
Проекция на ось Р полной скорости движения шара В случае неупругого воздействия рассчитывается ns Тип наклонной плоскости Масса неподвижной плоскости бесконечно велика, а скорость равна нулю, то есть m oo, vt 0. So. .У Проекция скорости центра тяжести шара в конце упругого удара равна, т .
Смотрите также:
Предмет теоретическая механика

