Оглавление:


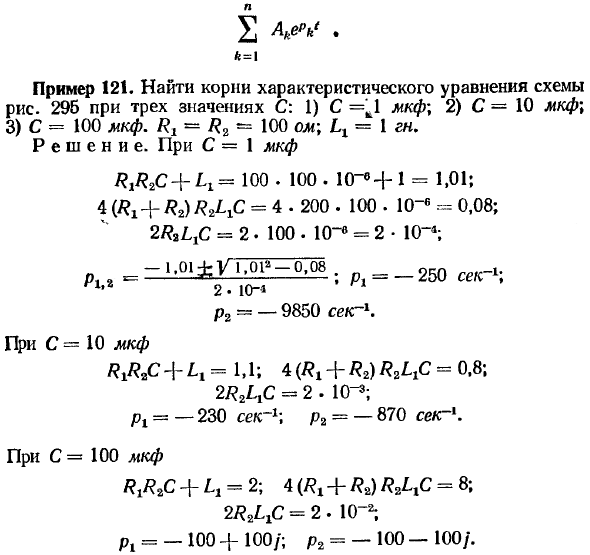

Составление характеристического уравнения системы
Составление характеристического уравнения системы. Число алгебраических уравнений равно числу неизвестных свободных токов. Положим, что р нам известно (в действительности оно пока не найдено и будет определено в дальнейшем), и решим систему (10.8) относительно ilce, i2ce и i3ce.
- Получим: Здесь Д есть определитель системы. В рассмотренном примере Z-1P + /?2 0 /?2 — 1 0 ц Ср At получается из определителя системы Д путем замены первого столбца правой частью уравнений (10.8):
Д2 получается из Д путем замены второго столбца правой частью системы (10.8). Людмила Фирмаль
Так как в правой части системы (10.8) стоят нули, то в каждом из определителей Др Д2 и А3 один из столбцов будет состоять из нулей. Известно, что если в определителе один из столбцов составлен из нулей, то этот определитель равен пулю.
Следовательно, Ах = — О, Д2 = О, А3 = 0. Из физических соображений ясно, что каждый из свободных токов не может быть равен нулю, ибо в этом случае не будут выполнены законы коммутации.
- Однако из предыдущего следует, что • _ £ 11«- д > Свободные токи могут быть не равны нулю только в том случае, если определитель системы А будет равен нулю: А = 0. (10.9)
При этом каждый из токов будет представлять собой неопределенность: At 0 . Д2_ 0 11гв~ д “ о ; д ~ о ; ’ раскрыв которую можно получить
действительное значение каждого свободного тока. Людмила Фирмаль
Раскрытием неопределенностей здесь заниматься не будем, а воспользуемся тем существенным для дальнейшего выводом, что определитель А алгебраизированной системы уравнений должен равняться нулю. Уравнение А = 0 называют характеристическим уравнением.
Единственным неизвестным в нем является р. В рассматриваемом примере после раскрытия уравнения А = 0 получим: ^ + /?2(£1р + /?1)+^^=0, или P2RjL\C 4- р (JRiRjC 4- £0 4~ ffi 4~ #2 п рС Если дробь равна нулю, то равен нулю числитель ее.
Следовательно, 4* р(^1^2^ + ^j) + ~ 0 (10.10) Корни квадратного уравнения: р ■ = ~ (R1R2C 4- £j) dhУТЖАзС 4~ £i)a — 4 (Rt 4- Ry) RyL\C 1,2 2/?АС • V • I В самом начале § 264 говорилось о том, что решение для свободного тока берется в виде Ае?’.
Если характеристическое уравнение будет иметь не один корень, а несколько, например, п9 то каждый свободный ток должен быть взят в виде fc=l
Пример 121. Найти корни характеристического уравнения схемы рис. 295 при трех значениях С: 1) С мкф; 2) С = 10 мкф; 3) С = 100 мкф. Rl — /?2 = 100 ом; Lx = 1 гн.
Решение. При С = 1 мкф R&C+L^ 100 . 100. 10-«+1 = 1,01; 4 (Ях+ Я2) R££ = 4.200 . 100 . 10“6 = 0,08; 2R2L£ = 2-100. 10“б = 2 • 10“; —1,01 j;Kl,Ql2 —0,08 . pt = — 250 сек»1; 2 . 10-1 р2~ — 9850 сект1.
При С — 10 мкф R&C + L^iA; 4 (/?х + Я2) ₽2LXC = 0,8; 2/?2LjC = 2 . IO»3; pt = — 230 сек1; p2 = — 870 сект’. При С = 100 мкф /?Х/?2С ~f-Lx = 2; 4(/?l + /?2)/?2L1C = 8; 2R2L1C = 2 . 10″2; рх = — 100 + 100/; р2 = — 100 — 100/.
Смотрите также:

