Оглавление:
| Здравствуйте! Я Людмила Анатольевна Фирмаль, занимаюсь помощью студентам более 17 лет. У меня своя команда грамотных, сильных преподавателей. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И неважно – она по объёму на две формулы или огромная, сложно структурированная, на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте. |
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Как получить помощь в выполнении заданий по сопромату
Вы можете написать сообщение в WhatsApp. После этого я оценю ваш заказ и укажу стоимость и срок выполнения вашей работы. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за вашу работу, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл готовой работы в личные сообщения.
Сколько стоит помощь
Стоимость помощи зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости, загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.
Какой срок выполнения
Минимальный срок выполнения составляет 2-4 дня, но помните, срочные задания оцениваются дороже.
Как оплатить
Сначала пришлите задание, я оценю, после вышлю вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Гарантии и исправление ошибок
В течение 1 года с момента получения Вами готового решения действует гарантия. В течении 1 года я и моя команда исправим любые ошибки.
Чуть ниже я предоставила примеры оформления работ по сопромату, то как я оформляю:
Пример помощи с задачей №1.4
Абсолютно жесткий (недеформирующийся) элемент Р укреплен на шарнирно-неподвижной опоре А и поддерживается стержнем l.
Определить наибольшую допустимую нагрузку F и перемещение т. С (рис. 1.6, а).
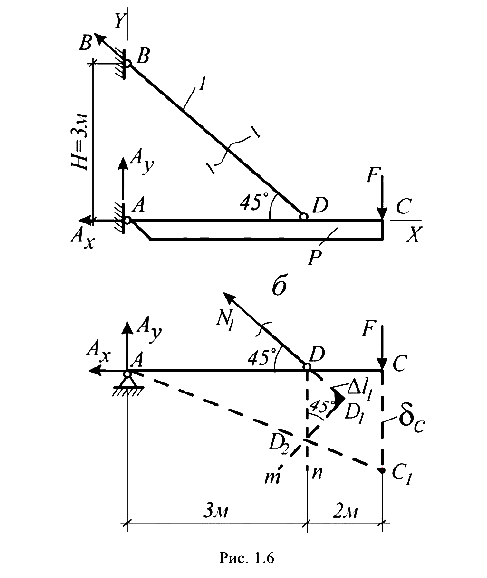
Стержень 1 — стальной, швеллер № 10. Для стали R = 210 МПа, Е = 200 ГПа.
Решение:
Нагрузка F через элемент Р и стержень 1 передается на опоры, где возникают три реакции (
, 
и 
— направленная по продольной оси стержня), которые могут быть определены из уравнений равновесия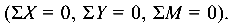 
Следовательно, рассматриваемая система является статически определимой.
По таблице сортамента площадь сечения швеллера № 10 (стержень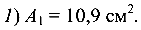 
Длина стержня
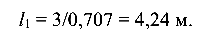
Так как стержень 1 соединяется с элементом Р при помощи шарнира, в нем возникает только продольная сила N, т. е. он подвергается деформации растяжения-сжатия.
Для определения продольной силы N система «рассекается» по стержню 1 и для рассматриваемой части системы составляются уравнения равновесия (рис. 1.6, б). Опорные реакци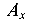и и 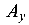для условия задачи интереса не представляют. Рациональным уравнением равновесия будет
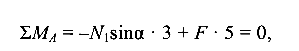
откуда
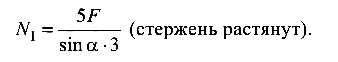
Максимально допустимая продольная сила в стержне 1 из формулы (1.2)
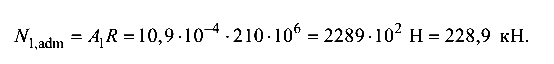
Наибольшая допустимая нагрузка на конструкцию (из уравнения равновесия)
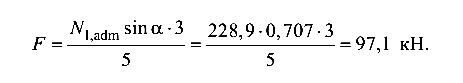
Абсолютная продольная деформация стержня 1 по формуле (1.3)
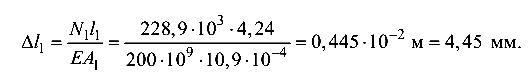
Абсолютно жесткий элемент Р под действием нагрузки F, вследствие деформации стержня 1, повернется вокруг шарнира А на некоторый угол.
Чтобы построить схему перемещений (рис. 1.6, б), стержень 1 следует мысленно отсоединить от элемента Р в т. D и по его направлению отложить отрезок, изображающий деформацию (удлинение)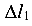 
,- получим т. 
.
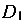Поскольку элементы системы должны перемещаться совместно, конец продеформированного стерня 1 (т.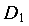 
) нужно свести с точкой D элемента Р.
Вследствие малых упругих деформаций можно допустить, что т. 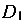перемещается по перпендикуляру к продольной оси стержня, т. е. по 
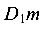. Точка D элемента Р по той же причине переместится по перпендикуляру к его продольной оси, т. е. по 
.
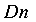Точка пересечения траекторий перемещений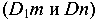 
дает т. 
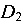-положение узла D в продеформированном состоянии системы.
Из подобия треугольников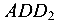 
и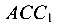 
составляется зависимость между перемещением 
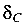и деформацией 
:
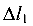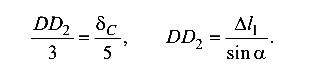
Тогда получим
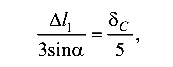
откуда перемещение т. С (вниз, по вертикали) будет
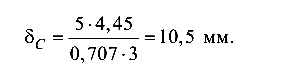
Возможно эта страница вам будет полезна:
| Предмет сопротивление материалов |
Пример помощи с задачей №3.4
Для сечения, составленного из двух прокатных профилей (двутавра и неравнополочного уголка), определить положение центра тяжести и значения главных центральных моментов инерции (рис. 3.6).
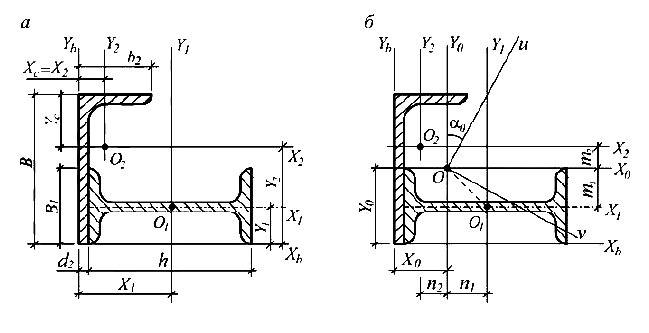
Данные к примеру: двутавр № 22, уголок № 20/12,5/1,1.
В рассматриваемом сечении двутавр расположен иначе, чем в таблице сортамента, поэтому значения моментов инерции нужно записать с учетом его положения.
Выписка из таблиц сортамента:
1) для двутавра № 22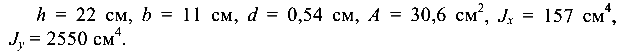 
2) для уголка № 20/12,5/1,1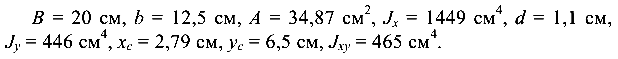 
Решение:
Сечение не имеет осей симметрии. Для определения координат центра тяжести сечения выбираются вспомогательные оси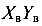 
; отмечаются центры тяжести фигур 
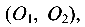составляющих сечение; проводятся их центральные оси 
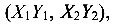параллельные вспомогательным, и вычисляются расстояния между ними и вспомогательными осями:
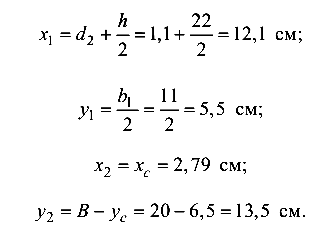
Координаты центра тяжести сечения
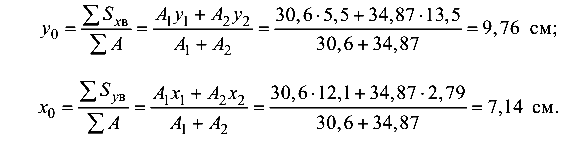
По значениям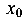 
и 
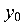на сечении отмечается центр тяжести О (рис. 3.6, б). Заметим, что центр тяжести должен лежать на прямой, соединяющей точк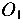и 
и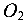 
.
Далее проводятся центральные оси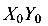 
, параллельные вспомогательным, и вычисляются расстояния п и т:
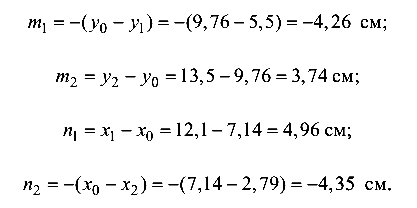
Знаки при т и п назначаются с учетом перехода от центральных осей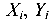 
, фигур, составляющих сечение, к общим центральным осям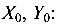 
Вычисляем значения осевых и центробежного моментов инерции сечения относительно центральных осей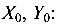
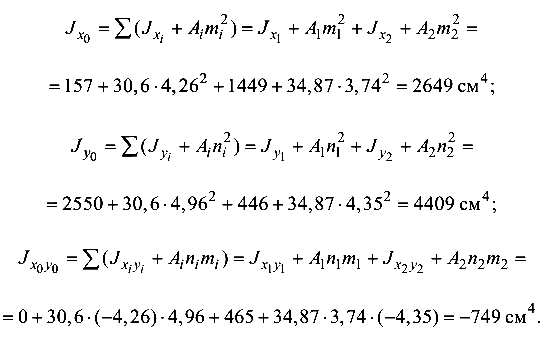
Значение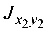 
положительное (см. рис. 3.1).
Положение главных центральных осей сечения характеризуется углом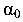 
, который определяется по формуле (3.3):
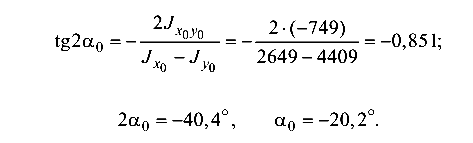
Угол 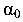отсчитывается от оси с большим моментом инерции, т. е. от 
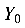, по ходу часовой стрелки, так как численное значение угла отрицательное. Таким образом определяется положение оси U.
По формуле (3.5) определяем значения главных центральных моментов инерции сечения:
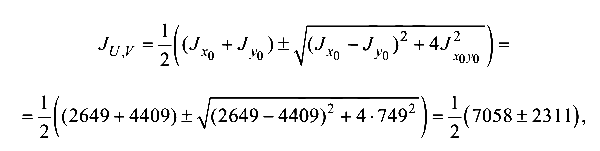
отсюда максимальный момент инерции сечения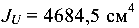 
, минимальный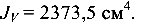 
Проверяем правильность вычислений, выполненных по формуле (3.5):
Таким образом, рассмотренное сечение имеет наибольшую сопротивляемость изгибу относительно оси U и наименьшую — относительно оси V.
Пример помощи с задачей №4.4
Стальной стержень кольцевого сечения скручивается моментом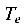 
. Определить наибольшее допустимое значение момента из условий прочности и жесткости, если 
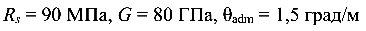(рис. 4.10).
Решение:
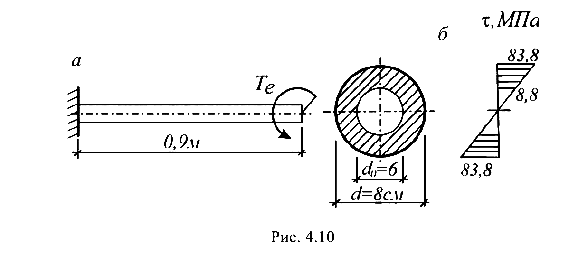
Вычислим геометрические характеристики заданного сечения.
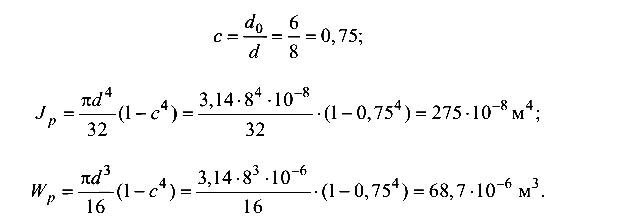
Допустимый относительный угол закручивания
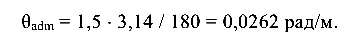
Из условия прочности (4.2) вычислим значение наибольшего скручивающего момента:
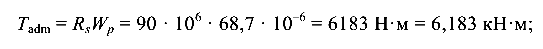
из условия жесткости (4.4)
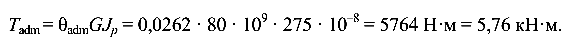
В качестве допустимого скручивающего момента принимаем его меньшее значение: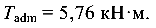 
Касательные напряжения на наружных и внутренних волокнах стержня вычислим по формуле (4.1):
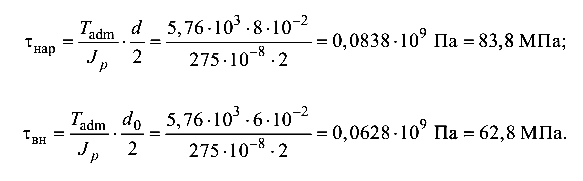
Эпюра касательных напряжений показана на рис. 4.10, б.
Пример помощи с задачей №4.5
Стальной стержень прямоугольного поперечного сечения скручивается моментом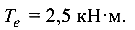 
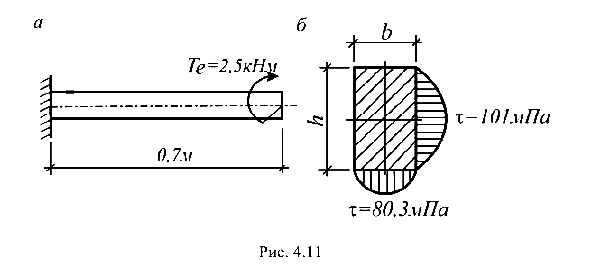
Определить размер сторон прямоугольного сечения (h/ b = 2,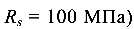 
и угол закручивания свободного конца стержня (G = = 80 ГПа), рис. 4.11.
Решение:
Геометрические характеристики заданного сечения
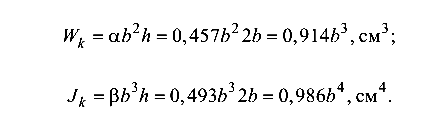
Наибольшие касательные напряжения по длинной стороне сечения
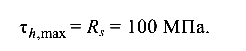
Из условия прочности (4.5)
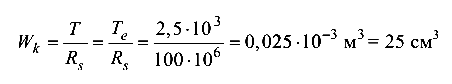
или
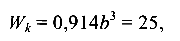
откуда b = 3,013 см.
Принимаем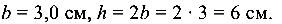 
Вычислим наибольшие касательные напряжения по сторонам сечения.
По длинной стороне
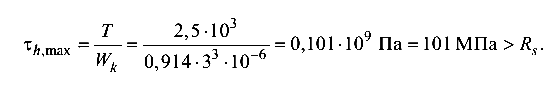
Перенапряжение составляет 1 %, что допустимо. По короткой стороне
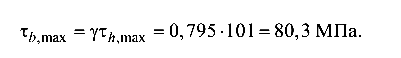
Эпюра касательных напряжений показана на рис. 4.11, б.
Абсолютный угол закручивания свободного конца стержня (по формуле (4.6))
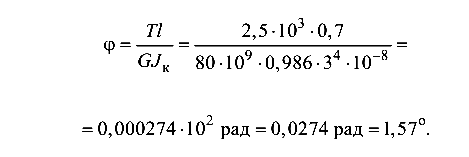
Пример помощи с задачей №5.5
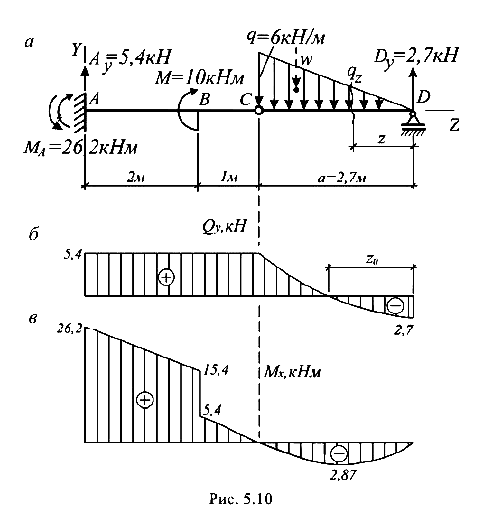
Построить эпюры Q и М для составной балки, нагруженной сосредоточенным моментом М и нагрузкой q, распределенной по закону треугольника, с максимальной ординатой q = 6 кН/м (рис. 5.10).
Решение:
В защемлении (сечение А) возникают вертикально направленная реакция 
и момент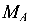 
а в шарнирной опоре D — реакция 
.
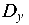Опорные реакции определяются из уравнения равновесия
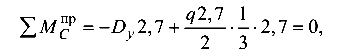
откуда
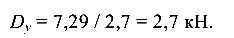
При определении реакции распределенная нагрузка была заменена равнодействующей, которая равна площади этой нагрузки (треугольника)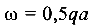 
и приложена в центре тяжести.
Плечо равнодействующей относительно сечения С равно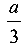 
:
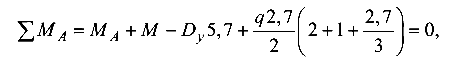
откуда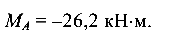 
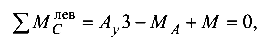
откуда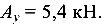 
Проверка:
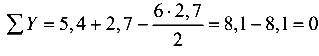реакции найдены верно.
Определяем внутренние силы (Q и М) в характерных сечениях балки.
Ход слева.
Сечение А:
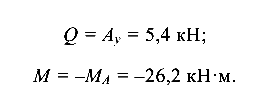
Сечение В:
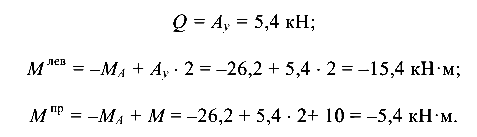
Сечение С:
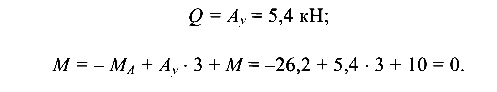
Для участка балки CD, где нагрузка носит сложный характер, составим подробные выражения для Q и М.
Ход справа:
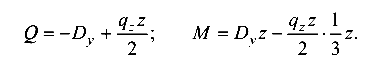
Ординату распределенной нагрузки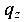 
найдем из подобия треугольников (нагрузочного и отсеченного):
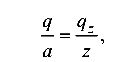
откуда
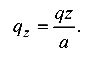
С учетом ординаты нагрузки 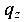получим
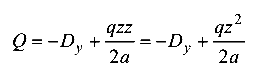
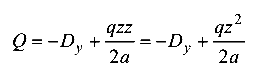-поперечная сила изменяется по квадратической параболе, обращенной выпуклостью вниз;
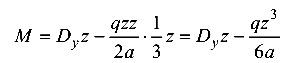
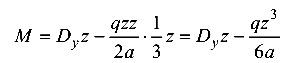— изгибающий момент изменяется по кубической параболе, выпуклостью вниз.
Чтобы установить направленность выпуклости эпюры, следует определить значения Q и М еще в одном сечении участка балки (лучше посередине).
Вычисляем значения Q и М на участке CD.
При z = 0
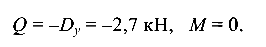
При z = 2,7 м
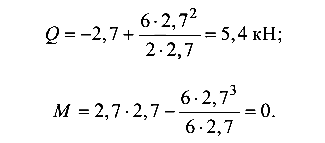
Эпюры Q и М показаны на рис. 5.10, б, в.
Для отыскания сечения, в котором Q = 0, нужно приравнять ее выражение нулю:
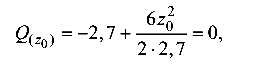
откуда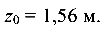 
При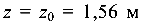 
максимальный изгибающий момент в этом сечении балки
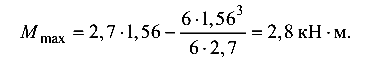
Из построенных эпюр внутренних сил следует, что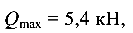 
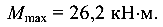
Возможно эта страница вам будет полезна:
| Примеры с решением по сопромату |
Пример помощи с задачей №5.8
Расположив сечение чугунной балки (рис. 5.16) рационально по отношению к нагрузке, определить ее наибольшее допустимое значение, если расчетное сопротивление на растяжение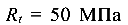 
, а сопротивление на сжатие 
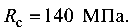Построить эпюры 
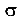и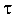 
.
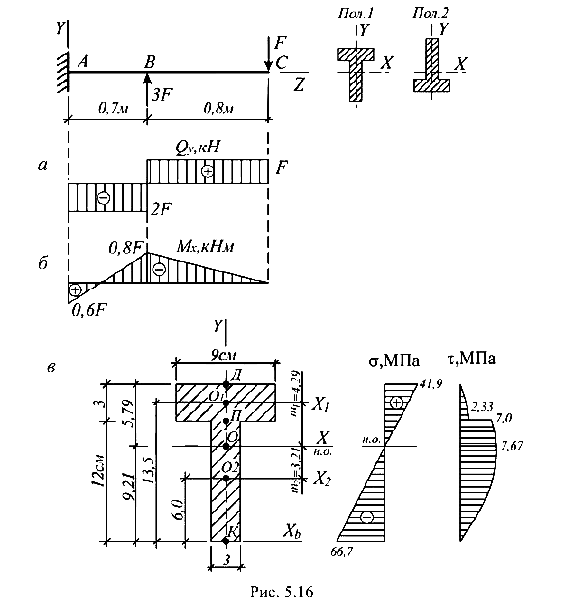
Для вычисления значений Q и М будем намечать сечения, начиная с правого (свободного) конца балки (ход справа). При этом не требуется определять реакции в опоре балки. Составим выражения для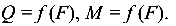 
Сечение С:
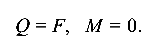
Сечение В:
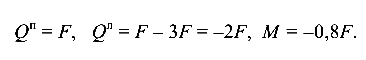
Сечение А:
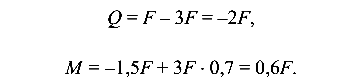
Определим геометрические характеристики сечения балки. Разделим сложное сечение на два прямоугольника. Положение центра тяжести сечения
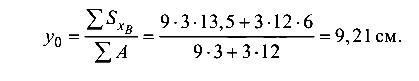
Осевой момент инерции
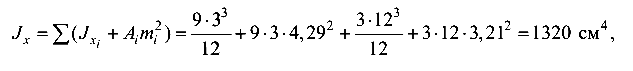
где
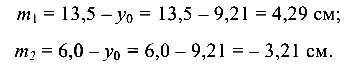
Статический момент части сечения, расположенной ниже нейтральной оси:
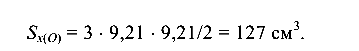
Статический момент части сечения, расположенной выше места соединения полки и стенки, относительно нейтральной оси (точка П):
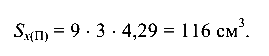
Наибольшую допустимую нагрузку на балку определим из условия прочности по нормальным напряжениям (5.3), учитывая разные значения расчетного сопротивления.
Опасным является сечение В, где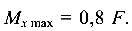 
В этом сечении верхние от нейтральной оси волокна растянуты (так как ординаты эпюры М лежат сверху), а нижние — сжаты.
Поскольку хрупкий материал балки лучше работает на сжатие, чем на растяжение, сечение нужно расположить так, чтобы в точке К были сжимающие напряжения, а в точке D, где сечение шире, — растягивающее. Это положение 1.
Рассматриваем принятое положение сечения (полкой вверх). Из формулы (5.3) наибольший изгибающий момент: по растягивающим напряжениям
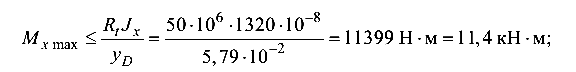
сжимающим напряжениям
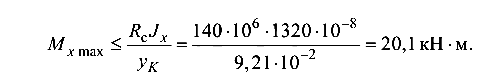
Чтобы обеспечить выполнение условий прочности по растягивающим и сжимающим напряжениям, в качестве наибольшего допустимого следует принять меньшее значение изгибающего момента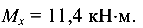 
Наибольшую допустимую нагрузку на балку определим из равенства
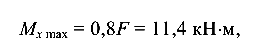
откуда F = 14,25 кН.
Следует проверить прочность по нормальным напряжениям в сечении А при принятом положении сечения балки и значении нагрузки F = 14,25 кН.
В сечении А
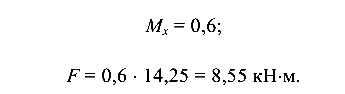
В точке Д (сжатие)
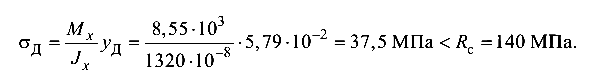
В точке К (растяжение)
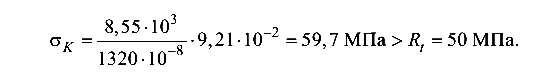
Условие прочности по растягивающим напряжениям не выполняется. Значит, значение нагрузки F следует скорректировать (уменьшить).
Из условия прочности по растягивающим напряжениям (как наиболее опасным)
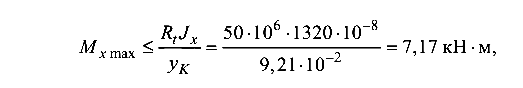
но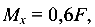 
откуда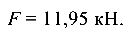 
Окончательно принимаем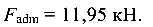 
Вычислим значения 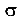и 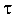, необходимые для построения эпюр напряжений. Для касательных напряжений опасным является сечение А, где
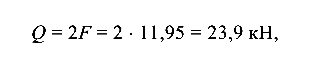
для нормальных — сечение В, где
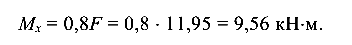
Нормальные напряжения в характерных точках сечения В
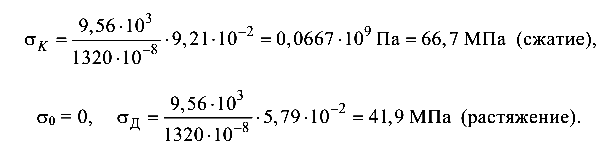
Касательные напряжения в характерных точках сечения А (по формуле (5.2)
Заметим, что в точке П ширина сечения изменяется скачкообразно. Вследствие этого также скачкообразно изменяется значение 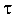(на эпюре скачок).
Эпюры 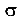и 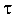приведены на рис. 5.16, в.
Расположив сечение балки полкой вниз (положение 2) и проделав аналогичные вычисления, получим меньшее значение допустимой нагрузки F = 9,5 кН.
Возможно эта страница вам будет полезна:
| Сборник задач по сопротивлению материалов |
Пример помощи с задачей №5.9
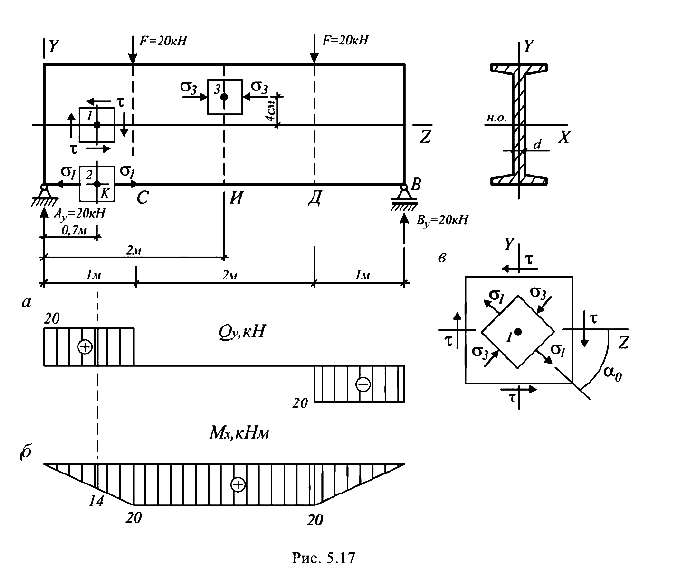
Определить главные напряжения в указанных точках балки (рис. 5.17) и установить вид напряженного состояния. Сечение балки -двутавр № 16.
Решение:
Из таблицы сортамента для двутавра № 16: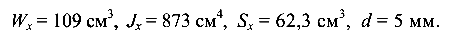 
Вследствие симметрии нагрузки опорные реакции
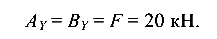
Эпюры Q и М показаны на рис. 5.17, a, б.
Заметим, что на участке СД балка подвергается чистому изгибу, так как на этом участке Q = 0.
В исследуемом сечении К
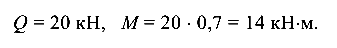
Для определения главных напряжений по формулам (5.1) и (5.2) необходимо вычислить значения нормальных и касательных напряжений в исследуемых точках сечения, а по формуле (5.6) — главные напряжения.
В точке 1
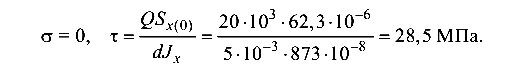
Экстремальные напряжения
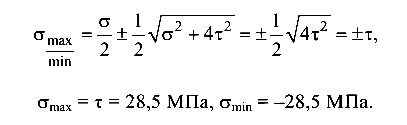
Главные напряжения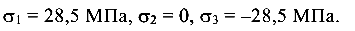 
В точке 1 балки имеет место плоское напряженное состояние, так как действуют два главных напряжения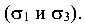 
Направление главных напряжений
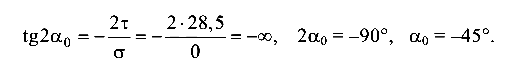
Угол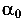 
отсчитывается от продольной оси Z. Отрицательное значение — по ходу часовой стрелки (рис. 5.17, в).
В точке 2
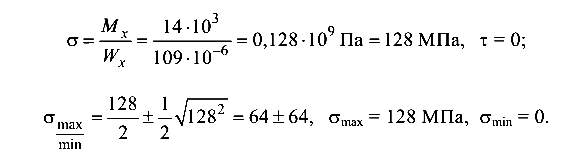
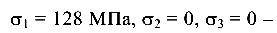— в точке 2 материал испытывает линейное напряженное состояние, так как действует только одно главное напряжение.
В сечении И балки Q = 0, М = 20 кН-м.
В точке 3
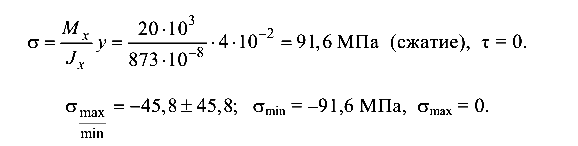
Главные напряжения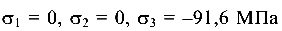 
— в точке 3 материал испытывает линейное напряженное состояние.
Если на участке СД балки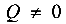 
(что чаще имеет место), то в точке 3 материал испытывает плоское напряженное состояние.
Пример помощи с задачей №5.14
Подобрать номер прокатного швеллера для двухконсольной балки из условия жесткости, если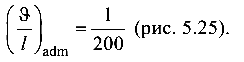 
Построить эпюру прогибов.
Решение:
Начало координат помещаем в крайнем левом сечении балки, т. е. на конце консоли (сечение О).
Значения опорных реакций и эпюра изгибающих моментов показаны на рис. 5.25.
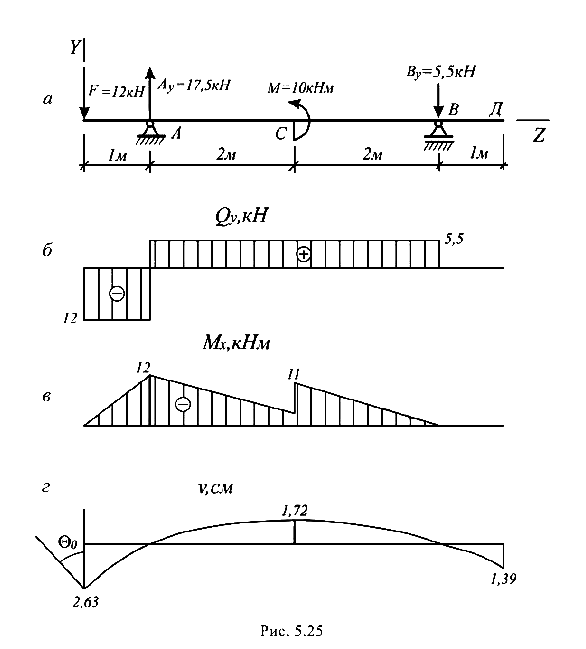
Рассматриваемая балка имеет четыре расчетных участка. Уравнение прогибов оси балки
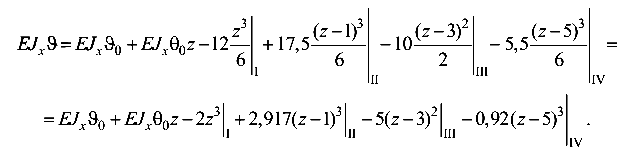
В данном случае, когда начало координат расположено на свободном конце балки, ни один из начальных параметров не равен
нулю. Значения их определим, исходя из деформативных условий на шарнирных опорах А и В, где вертикальные перемещения (прогибы) равны нулю: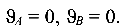 
Запишем уравнения прогибов для названных сечений. Сечение A (z = 1 м, участок 1)
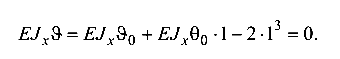
Сечение В (z = 5 м, участок 3)
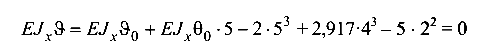
или
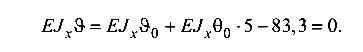
Из этих уравнений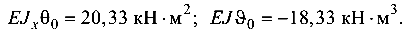 
Прогиб посередине пролета балки (z = 3 м, участок 2)
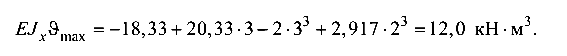
Требуемый момент инерции сечения для пролетной части балки
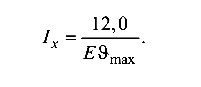
Примем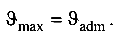 
Тогда из заданного условия жесткости
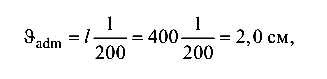
где l — длина пролета (расстояние между опорами). Для сечения из двух швеллеров
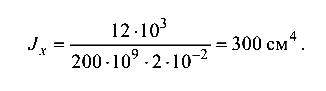
На один швеллер момент инерции составит
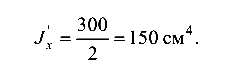
По таблицам сортамента принимаем два швеллера № 10, для которых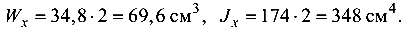 
Вычисляем прогибы в характерных сечениях балки. При z = 0 (сечение О)
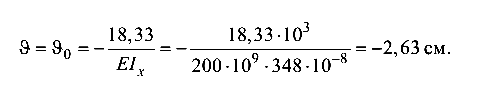
При z = 3 м (сечение С)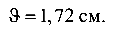 
При z = 6 м (сечение Д)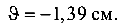 
По полученным значениям прогибов строится соответствующая эпюра (рис. 5.25, г).
Проследите соответствие эпюры прогибов эпюре изгибающих моментов.
Правая консоль балки (участок ВД) не нагружена и, следовательно, не деформируется. Ось ее остается прямой, но все сечения перемещаются за счет деформаций остальной части балки.
В завершение примера вычислим значения наибольшего нормального напряжения в балке:
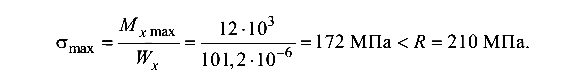
Прочность балки по нормальным напряжениям обеспечена, но материал ее недонапряжен на 18 %. Это обусловлено тем, что условие жесткости более «требовательно».
Возможно эта страница вам будет полезна:
| Учебники по сопротивлению материалов |
Пример помощи с задачей №9.4
Элемент конструкции Р, имеющий большую жесткость, укреплен шарнирно в опоре А и поддерживается двумя стержнями длиной l = 2 м и диаметром d = 4 см (рис. 9.7, а).
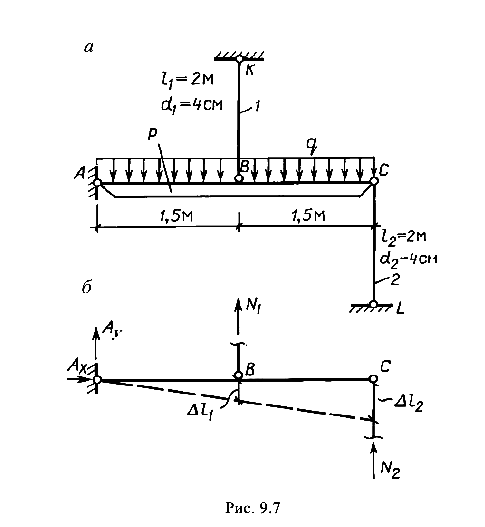
Определить наибольшую допустимую нагрузку q из условия прочности и устойчивости стержней, если R = 210 МПа.
Решение:
Нагрузка q, приложенная к элементу P, передается непосредственно на опору А и через стержни 1 и 2 на опоры К и L, где в сумме возникают четыре неизвестные реакции. Поскольку для плоской системы можно составить только три уравнения равновесия, рассматриваемая система является один раз статически неопределимой (4 — 3 = 1).
Для решения задачи нужно знать усилия в стержнях, выраженные через нагрузку q.
Мысленно рассекаем стержни и показываем продольные силы, направляя их с учетом характера деформации (рис. 9.7, б). Нетрудно понять, что стержень 1 растянут (усилие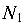 
направлено от сечения), а стержень 2 сжат (усилие 
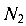направлено к сечению).
Вследствие деформации стержней 1 и 2 ось элемента Р повернется вокруг опоры А на некоторый угол. Уравнение равновесия
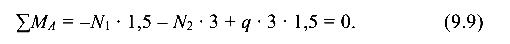
Уравнение деформации имеет вид
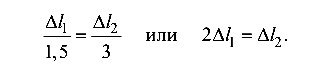
Используя формулу Гука, получим
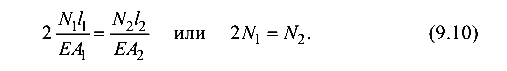
Поскольку стержень 2 подвергается сжатию, допускаемое усилие в нем должно быть определено из условия устойчивости (9.7) Характеристики стержня: площадь сечения
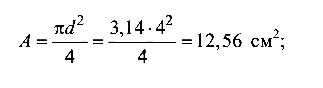
момент инерции
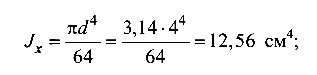
радиус инерции
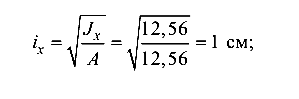
гибкость
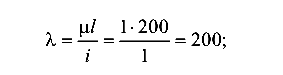
коэффициент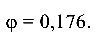 
Наибольшее допустимое усилие во втором стержне из условия устойчивости
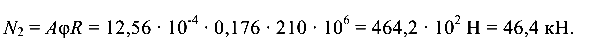
Из равенства (9.10)
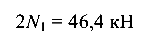
усилие в первом стержне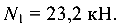 
Из уравнения (9.9) наибольшая допустимая нагрузка на систему
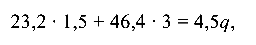
откуда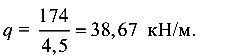 
Действующие напряжения в стержнях системы и сопоставление с допускаемыми:
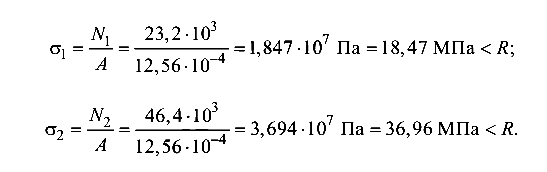
Допускаемое напряжение во втором стержне
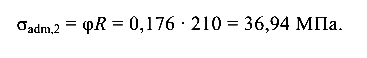
При нагрузке q = 38,67 кН/м прочность и устойчивость стержней обеспечены.
Кстати у меня есть готовые задачи на продажу, если нужно они вот тут.
Пример помощи с задачей №9.7
Балка длиной l = 6 м с шарнирными опорами, выполненная из двух швеллеров № 22, нагружена поперечной равномерно распределенной нагрузкой q = 5 кН/м и продольной силой ,F (рис. 9.11, а).
Определить наибольшую допустимую продольную нагрузку F, расположив сечение швеллеров рационально (вариант 1, 2 или 3).
Проверить прочность и жесткость балки при принятом варианте, если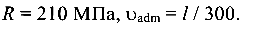 
Решение:
Балка подвергается продольно-поперечному изгибу.
Сначала надо выявить рациональное положение сечения балки по отношению к поперечной нагрузке, т. е. при изгибе. Затем определить наибольшую допустимую продольную нагрузку из условия устойчивости балки при различных вариантах расположения ее сечения и только после этого принять рациональное положение сечения балки и проверить ее прочность и жесткость
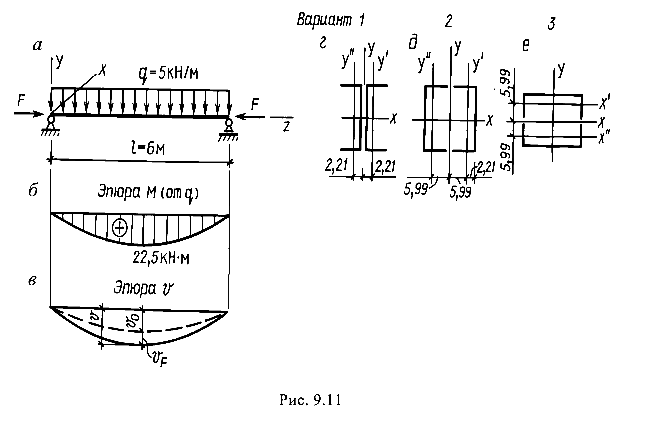
Геометрические характеристики швеллера № 22
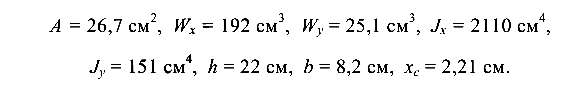
Эпюра изгибающих моментов от поперечной силы показана на рис. 9.11, б. Максимальная ордината эпюры в середине пролета
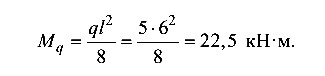
Деформированная схема балки показана на рис. 9.11, в. Рассмотрим первый вариант расположения сечения (рис. 9.11, г). Вычислим геометрические характеристики сечения относительно главных центральных осей:
площадь
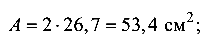
момент сопротивления
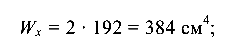
моменты инерции
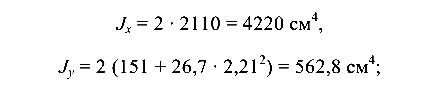
радиусы инерции
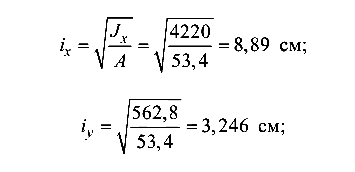
гибкость балки
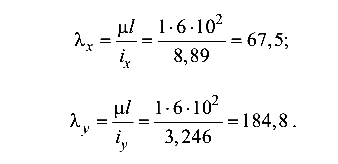
Заметим, что по условию закрепления концов балки коэффициент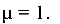 
Анализируя значения гибкостей балки (можно также и моментов инерции сечения) видим, что гибкость относительно оси Y больше, чем относительно оси X. Значит, потеря устойчивости возможна относительно оси Y, в направлении оси X.
Для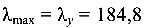 
по таблице 
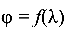коэффициент продольного изгиба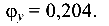 
Наибольшее допустимое значение сжимающей продольной силы из условия устойчивости (9.8) будет
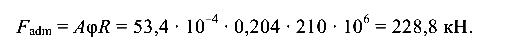
Рассмотрим второй вариант расположения сечения (рис. 9.11,д). Геометрические характеристики сечения:
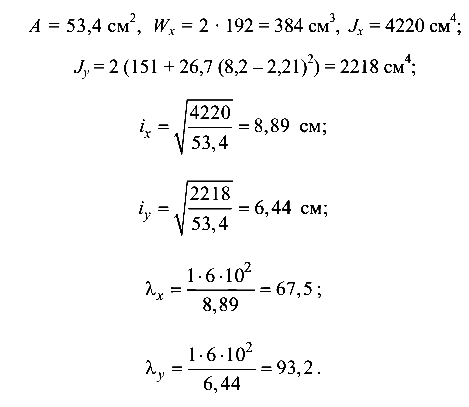
Для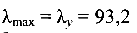 
коэффициент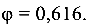 
Наибольшая допустимая продольная сила
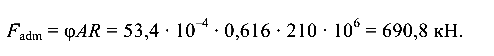
Рассмотрим третий вариант расположения сечения (рис. 9.11, ё). Геометрические характеристики сечения:
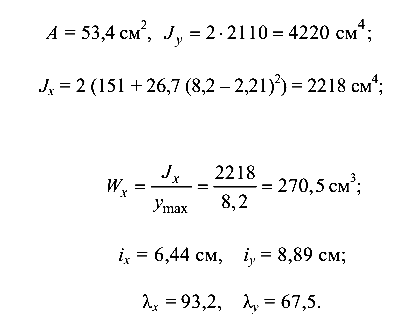
Для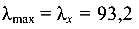 
коэффициент 
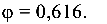Наибольшая допустимая продольная сила
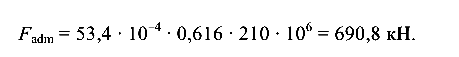
Из результатов вычислений следует, что: для продольной сжимающей силы F рациональными будут варианты 2 и 3, так как допускаемая нагрузка для них большая, чем в варианте 1;
для поперечной силы q рациональным будут варианты 1 и 2, поскольку момент сопротивления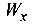 
в этих случаях больший, чем в варианте 3;
для дальнейшего расчета принимаем расположение сечения балки по варианту 2, при котором будет наибольшая сопротивляемость как поперечному, так и продольному изгибу.
Проверим жесткость балки в принятом варианте расположения сечения.
Максимальный прогиб будет в середине пролета балки (см. рис. 9.11, в).
Прогиб от поперечной нагрузки
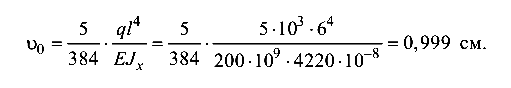
Эйлерова сила
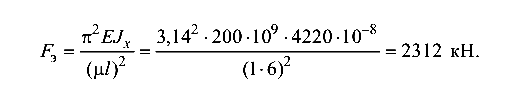
Полный прогиб балки
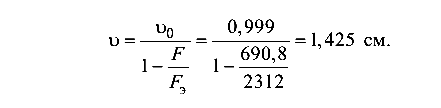
Так как полный прогиб 1,425 см меньше допустимого
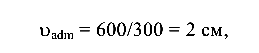
жесткость балки обеспечена.
Проверим прочность балки от совместного действия поперечной и продольной нагрузок.
Максимальный изгибающий момент в балке
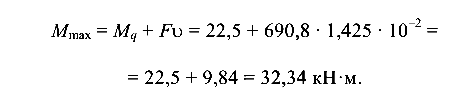
Максимальное нормальное напряжение в балке
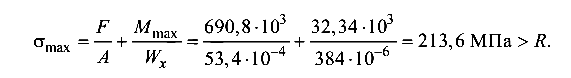
Перенапряжение в балке составляет 1,71 %, что допустимо. Таким образом, положение сечения балки по варианту 2 удовлетворяет требованиям по жесткости и прочности.
