Оглавление:


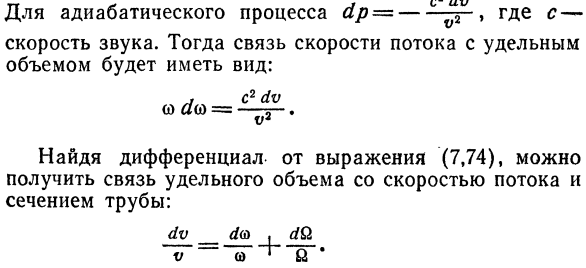




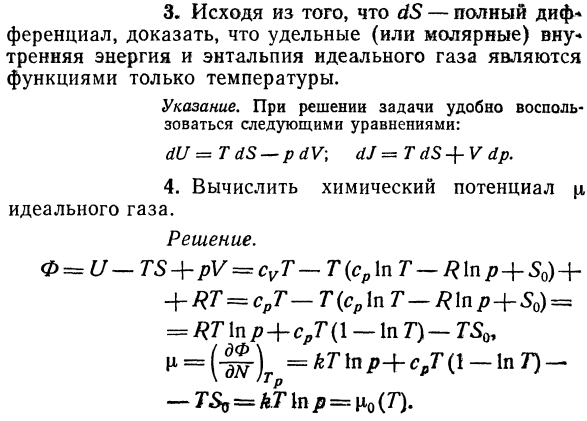

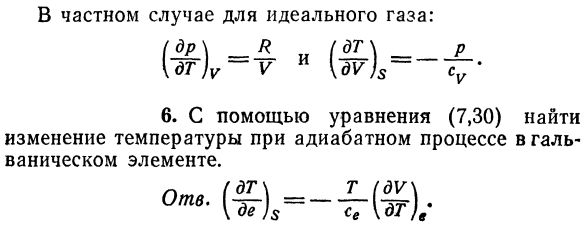








Сопло Лаваля.
- Сопло Лаваля Технология часто является обязательным условием Бизнес. Подача газа или пара через pipe. At в то же время Они постоянно стремятся получить поток газа с очень высокой скоростью, использовать его кинетическую энергию Энергия турбины или реактивного двигателя. Для случая Поток газа по трубе переменного сечения Следующее соотношение: = const, G, 74) Где Q (x) — поперечное сечение
трубы, co (x) — расход газа、 v (x) — удельный объем, изменение координат x По трубе. За счет уменьшения и увеличения площади поперечного сечения трубы、 Однако、 Коническая труба не смогла набрать скорость Поток, который превышает «локальную» скорость звука в трубе.
Когда давление увеличивается, оно может быть сколь угодно большим Расход газа. Людмила Фирмаль
Рассмотрим течение газа по трубе с большой скоростью Speed. In в этом случае происходит теплообмен со стеной Игнорировать, т. е. мы можем предположить, что процесс продолжается Адиабатический: dS-Q. но вы также должны рассмотреть Кинетическая энергия газового потока. Таким образом, полный
Энергия газа равна: ^ ^ Г, 75) B2 (JC)) Где-кинетическая энергия 1 моля газа. Полное изменение энергии должно быть равно нулю、 То есть, если dS = 0: / > 2 без) Для процесса изоляции dp=^ -, где c〜- Скорость sound. In поворот, расход потока и специфический Объем должен выглядеть так: Если вы найдете разницу между Формулой G и 74)、 Получить отношение между определенным объемом и потоком、 Секция трубы: дифференциальный клапан в Сто семьдесят один
- Последние 2 выражения Соединение площади поперечного сечения трубы с расходом: 1Т 9 9Н день С2 дю(—а、 — К-c2Og = ^ — г. Г, 76) Изучите выражение лица result. To рассмотрим Коническая труба-r — <0, предполагая начальную скорость Поток меньше скорости звука c 0, то есть Скорость потока увеличивается при движении по трубе Так и будет increase. In этот случай, этот момент должен наступить Скорость CTaHet равна скорости звука: co = s. справа.
Часть уравнения отрицательна. ^д Поскольку равенство имеет смысл,〜t-должно быть равно ±oo. In кроме того, скорость co остается меньше, чем c、 , движение Замедленная съемка. Использовать только Сплющенное сопло не может получить расход потока Больше скорости звука.
Поток ускорится, но скоро Поток превышает скорость звука Людмила Фирмаль
Скорость потока СО = с* На критической скорости. Если расход потока Дю. Равная скорости звука-j — будет равна нулю. Как видно из уравнения G, 76),〜может оставаться дольше Ноль. Когда поток проходит через критическую скорость、 Скорость участка трубы в будущем будет увеличиваться. После этого расход потока продолжается к increase. So … Для очень высоких расходов газа
Необходимо использовать трубы определенной конструкции Конструкция; сначала сужение, затем расширение. Эта труба формы используемая для ускорения газа Поток газа называется соплом Лаваля. Ускорение ха Поток газа в таком сопле будет только возникать — Если^ = 0, то расход равен Точно равна критической скорости. Это достигается за счет Специальный расчет режима работы сопла Лаваля 、
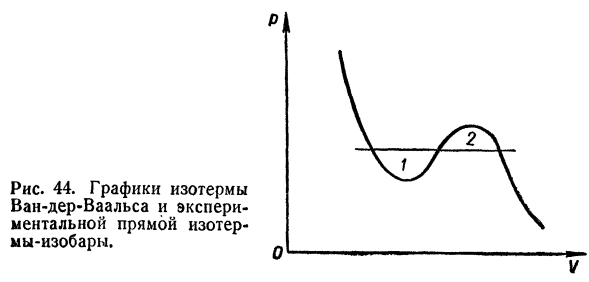
Задачи и упражнения 1. тер-с использованием основной формулы Установите правило термодинамики, Максвелл. pV рисунок (рисунок 44) Пересечение изотермы ван-дер-Ваальса является экспериментальным Применимо к экспериментальной линии, изотерме и изобарной линии Равновесие газожидкостной системы такое же. Решение. Первый и второй закон Термодинамика дает: При применении к изотермическим циклам: T j dS ^ jdU + J pdV.
Однако, поскольку J dS = 0 и J <W = 0、 Итак, сайты 1 и 2 одинаковы. 2.Вычислить термодинамическую функцию В случае равновесного излучения V, F, J, Ф. Решение. Функции U, F,/, функции как тепло Термодинамическая функция должна быть выражена соответствующим образом Каждая переменная: U = U(S, V), F = F(T, V),/ = /(Sf / 0,Φ=Φ(T, p). Для равновесного излучения U = uV, где и-плотность Плотность энергии, закон Стефана-Больцмана равна oT4, следовательно U = T4V Рис.44.
Сюжет изотермы Ван-дер-Ваальс и эксперименты Прямой изолятор для экспериментов Изотермы-Изобары. В Сто семьдесят три Представлять выражение в переменной S и 1/, T должны быть выражены в S и V. Из уравнения лучистой энтропии s — joT3V Мы это выясним: И затем С W Свободная энергия: Ф = ц-ц = ВЗ * в-Т〜- Энтальпия: Джей = от U + рv = — отъ * В = Ц ^ С(?Fju. Гиббс: термодинамический потенциал : = — ±
Это происходит потому, что термодинамический потенциал Гиббс Φ (T, P) не поддается равновесию Функции радиационной тепломеханики. Это дело в том, что Р и Т не являются независимыми от излучения Переменная: Один 3, предполагая, что dS является идеальным дифференциалом* Ференциал, оказывающийся специфическим (или молярным) внутри* Идеальная газовая головка, энергия и энтальпия Единственное что работает-это температура. Решая проблему симптома, удобно использовать
Используйте следующее уравнение: дю = * ТДС-ПДВ; диджей = zTdS + в ДП. 4.Вычислите химический потенциал Идеальный газ. Решение. Сто семьдесят четыре 5.Используя уравнения термодинамики G, 30) найти температурные изменения в изоляции Расширение и сжатие тела(в общем и целом Идеальный газ.) Решение. Поставим уравнение G, 30) x = V и*/=/? дв)х〜\ ДС) в *
Или согласно началу термодинамики II: дв)х-л \ йй) в * Потому что правая часть указывает на постоянный объем Он тогда d’Q dT дециграмм ^ Л / Ил \ Или, согласно соотношению а, 3): ДТ \ т {р (дв Последнее выражение является желаемым выражением. \ — gy \ <0, поэтому т0-признак изменения температуры Противоположный знак коэффициента теплового расширения Рения в:
Частный случай идеального газа: \ dT) v-V и \ dV) s—7 ^ ’ 6.30) поиск с использованием уравнения G Изменение температуры в процессе изоляции Гальванический элемент. — (?Я не уверен.- ?¦(*).- 7.Используя выражение G, 31) получаем Температурная зависимость поверхностного натяжения. Н-да-л (йд \ 8.С этой свободной энергией Термодинамический потенциал идеального газа Резюме, которое«А-БТ равна: «- ’- Ноги 9.
Показать его 10.Покажите это, когда вы двигаетесь Другая модификация (например: олово или кварц) Определенная свободная энергия обеих модификаций равна Среди них. Решение. Полная свободная энергия Обоих изменений при температуре перехода 1. Другое изменение равно следующему: Где Fi и f2-собственные свободные энергии каждого из них Изменить.
Рассматриваемая система является закрытой, и поэтому общее Другими словами, изменение свободной энергии равно нулю ДФ = FX с протоколом DMX-Ф Ф2 дм2 =0.Г, 77) Масса системы остается неизменной. м = МХ + м2 = const и Так… Или управление DMX = — дм2 Соотношение G, 77) можно переписать в виде: rfm1 (F,-JF2)= 0, G, 78) Откуда ft = F2, c1m {Φ0. 11.Доказать родство: \ дв ЯТ— ’ ДТ * СП Ф-г. ДП ч〜
Примечание, 2-й должен быть использован Начало термодинамики дифференцирования Форма, определение удельной теплоемкости и корреляция Взаимное отношение G, 31)\ G, 33). 12. указывает, что cp-cv-R является идеальным Идеальный газ используя термальную функцию. Решение Это известно И затем… •(?Я не уверен.-» ¦ 13. покажите, что cp и cv идеальны Газ не зависит от p и V. Обратите внимание, что вам нужно использовать Соотношение! Я дв)Т-XST ^ / в ’\ тр)т ==〜’
И уравнение состояния* 14.Свобода слова Свободная энергия идеального газа (см. Задачу 8), найти уравнение Уравнение состояния идеального газа. Показания должны использоваться соответственно* Решение G, 13}. 12 В. Ф. Ноздрев 177 15.На основе уравнения: И уравнение G, 30), которое приводит к соотношению: 16.Найти отношения темпелла-* Круглая инверсия и критическая температура Газ. Решение. Полученный* Г, 71): ОД. SR Из уравнения ван-дер-Ваальса Р ДТ) Р-p_a, 2ab ’
Предположим, что вы получаете выражение G с V ^> b и RTV ^ > 72) В форме: — АКДС П Где cp-молярная изобарная теплоемкость газа. ??ГИнв = 0.、 2а A_p. Т-2а −5 = О-У, 1 инв—ПГ• * \ 1 inv как? Используя формулу критической температуры Реальный газ Tk — > — и нашел формулу Инверсия температуры, мы получаем: 6.75 ГК. инв = 6,75 ГК.
Таким образом, фактическая инверсия температуры ha Звоните (Ван-дер-ваальсовыми) составляет 6,75 раза больше критического Температура.17.Указывает, что изменение является динамическим Кинетическая энергия газового потока при прохождении через сопло Любая форма определяется разницей в энтальпии Начальное и конечное состояние газа. Необходимо использовать знаковое выражение Г, 75).
Смотрите также:
Решение задач по термодинамике
| Свободная энергия равновесных систем. | Учение о термодинамическом равновесии в сложных системах. |
| Тепловая функция. Эффект Джоуля Томсона. | Правило фаз Гиббса. |

