Оглавление:



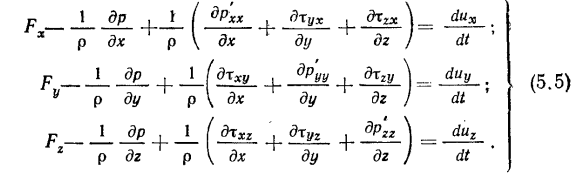

Соотношения между напряжениями и скоростями деформаций в движущейся вязкой жидкости.
Соотношения между напряжениями и скоростями деформаций в движущейся вязкой жидкости. Связь между касательным напряжением m и скоростью деформации жидких частиц основана на законе внутреннего трения Ньютона (1.12).Где Р-динамическая вязкость. yi / yp-градиент скорости, перпендикулярный направлению движения. Закон Ньютона применим только к ламинарным течениям. Знак плюс или минус Li выбирается таким образом, чтобы значение m было положительным, независимо от выбора положительного направления n. Любовь. Вверх. АВ А( Иначе говоря икс ±В Ав_ А1.
Этот же опыт дает распределение скоростей жидкости: на неподвижной пластине скорость жидкости равна нулю, на верхней — равна скорости пластины. Людмила Фирмаль
- Градиент скорости при слоистом движении жидкости представляет собой скорость угловой деформации частиц Распространяя закон вязкого трения на трехмерное (пространственное) движение, получаем следующее уравнение для тангенциального напряжения: (5.2) 92. В каждой точке движущейся вязкой жидкости, помимо напряжения в тангенциальном направлении, существует напряжение в нормальном направлении, величина которого зависит от направления действия.
Вертикальное напряжение имеет следующие характеристики: сумма значений перпендикулярных напряжений, действующих на 3 взаимно перпендикулярных участка, инвариантна и не зависит от выбора участка. Исходя из этой характеристики, учитывается скалярное значение. Это давление движущейся жидкости, которое определяется как среднее арифметическое нормальных напряжений в определенной точке, действующих в 3 направлениях перпендикулярно друг другу. _ + Ruu +РГГР3 Очевидно, что зависимость нормального напряжения от направления действия, наблюдаемого в вязкой жидкости, является результатом выражения вязкости.
- В зависимости от вязкости нормальное напряжение выражается давлением р и некоторыми дополнительными напряжениями. (5.3) Рхх—Р+Рхх’, Руу =Р+ Руу)Ргг= —Р +Ргг、 Здесь r’xx, r’YY, r’y-дополнительные вертикальные напряжения, обусловленные действием вязких сил. Эти дополнительные напряжения зависят не от величины давления, а от направления действия. Знак минус перед давлением p означает, что направление давления p всегда совпадает с внутренней нормалью соответствующей грани выделенного объема (в объеме).
Как уже указывалось, принято считать значения pxx, ruu и rrg положительными, если они соответствуют соответствующим внешним нормалям грани. 2С. Ров. ЦТ. 93. Для вязких несжимаемых жидкостей дополнительное напряжение, P xx * p’Yu * Prg, является прямым 0, что пропорционально соответствующей скорости деформации (относительному удлинению), а коэффициент пропорциональности равен 2c. 2(. Копать дециграмм. Rxx. Вот именно. Ух. П + 2С th. * п + 2 [х ^-. ;Р + 2р、 ЮУ. (5.4) дециграмм. И затем.
В соответствии с рассмотренным опытом можно вывести связь между тензором напряжений и тензором скоростей деформаций в общем случае. Людмила Фирмаль
- Если частичная производная положительна, то соответствующее дополнительное напряжение за счет действия вязкой силы будет растягивающим, а при отрицательном значении-сжимающим. Наконец, о вертикальных и касательных напряжениях вязких и несжимаемых жидкостей. Как видно из закона крюка, следует отметить, что для твердого (упругого) тела напряжение пропорционально соответствующей относительной деформации. Для вязких жидкостей, напряжение пропорционально скорости деформации.
Смотрите также:
Возможно эти страницы вам будут полезны:
- Напряжения в движущейся вязкой жидкости.
- Уравнения движения вязкой жидкости в напряжениях.
- Соотношения между напряжениями и скоростями деформаций в движущейся вязкой жидкости.
- Уравнения Навье — Стокса.
- Уравнение Бернулли для элементарной струйки (для линии тока) вязкой жидкости при установившемся движении

