События

События

• Событие Одним из основных понятий теории вероятностей является случайное событие или, как мы часто говорим, просто событие. В реальном мире случайные события — это результаты (тесты, наблюдения, эксперименты), которые могут происходить (происходить, происходить) или не происходить (происходить, не материализуются).

• Пример 1. При броске костей 1) количество очков совпадает с любым числом в наборе из 1, 2, 3, 4, 5, 6 чисел. Событие в этом случае, например, L = {четное количество очков отсутствует}, B = ■ {отбросить количество баллов в течение 3}. Математические модели могут принять концепцию события в качестве исходного.

Он не определен и характеризуется только своими характеристиками. Людмила Фирмаль

Основываясь на реальном значении концепции события, вы можете определить следующий конкретный случай концепции события и следующее действие над событием. Всегда предполагайте, рассматриваете ли вы несколько событий одновременно Эти события могут или не могут произойти для одного теста того же теста (то есть, в тех же условиях). Надежные события называются событиями, которые всегда происходят и обозначаются th.

Невозможные события — это события, которые никогда не станут propshfdnt. Определяет невозможное событие 0. Событие А называется противоположным событию А, ‘) Кости называются кубиками из однородного материала, а их грани пронумерованы 1, 2, 3, 4, 5, 6. Количество очков, выпадающих при броске костей, — это число в верхней части куба.

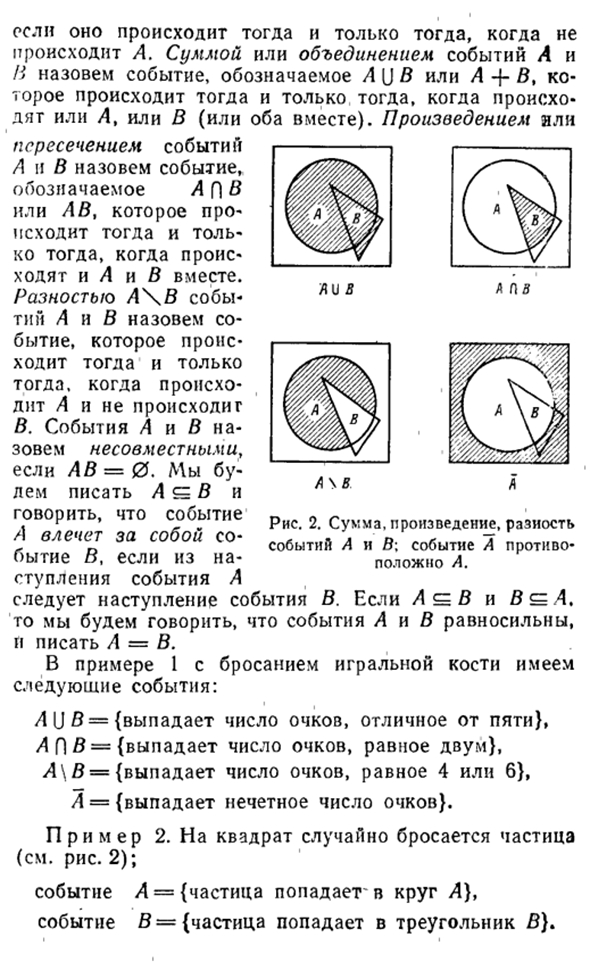
Сумма или комбинация событий A и I означает событие, обозначенное A [) B или A + B%, и происходит только в случае, когда A или B (или оба) вместе). Цена продукта и Пересечение событий A и B является событием, обозначенным A P B или L B, и происходит только тогда, когда A и B происходят одновременно. Событие A \ B Разница A \ B — это событие, которое происходит, только когда происходит A, а B не происходит.

• Если AB = 0, события A и B несовместимы. Событие A сопровождает Событие B, если Событие A следует за событием B. В случае A ^ B и B ^ события Liv называются эквивалентными и A = B. Пример 1 броска костей имеет следующие события: LUB = {уменьшить количество точек, отличных от 5}, LPB = {уменьшить количество точек, равное 2}, A \ B = {уменьшить количество точек, равное 4 или 6}, L = {нечетное количество точек падать}.

Пример 2. Событие A = {частицы попадают в круг A}, событие B = {частицы попадают в треугольник B}. (L X / ^ y / PP Будь или нет A \ B Рисунок 2. Событие A и B итог, продукт, разница \ Событие A противоположно A. Событие A [) B, A (в этом случае \ B, A \ B и A — частицы, соответствующие области, полученной путем объединения и пересечения различий между квадратными областями A и B и дополнением A (соответствующей областью Затенены на рисунке 2).

Частицы случайным образом выбрасываются в квадраты (см. Рисунок 2). Людмила Фирмаль

В настоящее время в теории вероятностей наиболее распространенным подходом является определение события с помощью неопределимой концепции базового события. Наиболее распространенной стохастической моделью в простом случае является модель n. Предположим, что есть кость n с таким же шаром n. Тест случайным образом выбирает один мяч из ур. & 2 = {u> i, <02. <*> • «}

Множество шаров в урне для голосования. Если вы взяли мяч o>, eL из шара во время теста, A является подмножеством набора шаров Q и говорит, что событие A произошло; w, Если ^ A, мы говорим, что событие A не произошло, и в этом случае событие A идентифицируется подмножеством (-1) из набора всех возможных результатов.

В общем случае мы рассматриваем несколько базовых множеств Q = {o>} в каждой теоретической вероятностной модели. Элементы называются элементарными событиями, само множество Q называется элементарным пространством событий, а часть подмножества A ^ Q называется событием. Операции с событиями — это операции над подмножествами. В то же время теория вероятностей использует свои собственные термины.

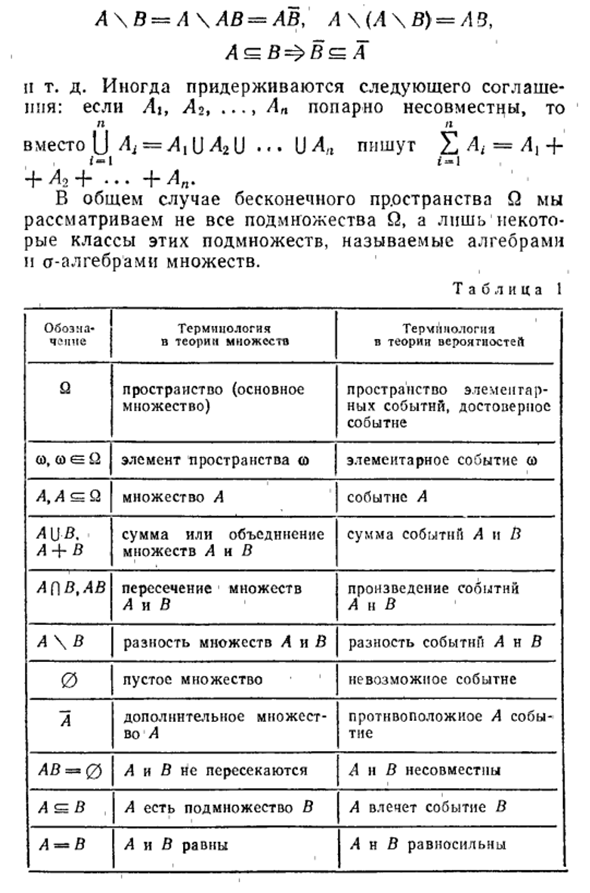
Таблица 1 показывает взаимосвязь между этим и терминами в теории множеств. Сумма и произведение событий могут быть расширены до конечного или бесконечного множества событий [] La% f) Aa. Общая собственность 1 Вы есть Радио на съемочной площадке будет перенаправлено на операцию события. Например, 1PG = P TTZ = 1Ua, 1 = L, a a a a A = Q \ A, 0 = Q, U = 0, A \ D = A \ AB = AB} A \ (A \ B) = AZ, A ^ B = $> B ^ A

Время от времени они придерживаются следующего соглашения: если At, A2, Ln не являются попарно совместимыми, н н (Вместо J Ai = ,, U 2 2 U ••• U A, напишите X ,, = ,, + / -1 1 + A> + … + Ap. В общем случае бесконечного пространства Q мы рассматриваем не все подмножества Q, а только некоторые классы этих подмножеств, называемые алгебрами и а-алгеброй множеств.

Таблица 1 Обучение вагонам и терминология терминов теории множеств в теории вероятностей Пространство Q (основной набор) — это пространство для события zlemengar доверенного события. (|), (Пятый элемент в пространстве элемента события <о Установить событие A A [) B. A — \ — сумма или комбинация множеств A и B является суммой событий A и B A (]

Пересечение множеств BtAB A и B является произведением событий A1! B. Установить A и B A \ B разница Событие A и B разница 0 Пусто установлено невозможное событие А дополнительный набор А является противоположным событием А AB = 0 A и B не пересекаются, A и B не совместимы A <= B A является подмножеством B A с событием B A = B A и B равны A, а B равен.

Определение 1. Класс si подмножества Q называется алгеброй множеств, если: 1) £ 2 <=. P /; 2) Le ^ от A e j /; 3) Продолжать с А, Бе против Определение 2. Множество алгебры на называется о-алгеброй, если оно следует из / 1 = 1, 2, …. U L.E.s /, P л-1 л »1

Смотрите также:

Предмет теория вероятностей и математическая статистика

Независимость случайных величин	Вероятное пространство
Предмет теории вероятностей	Конечное вероятностное пространство. Классическое определение вероятности