Оглавление:




Смещение при оценке одновременных уравнений
- Смещение при оценке одновременных уравнений Ошибка измерения — не единственная причина четных чисел Условие Гаусса-Маркова. Причиной может быть смещение, порог Учитывая систему уравнений, этот случай Пример. Предположим, вы оцениваете параметры уравнения функции Ленивость в простой кейнсианской модели получения дохода: C = a + pG; + 1 / ,; (11,1) Y = C + 1G (11,2)
- Эта модель показывает закрытую экономику без вмешательства правительства. Модель использует традиционную спецификацию системы национальных счетов Где Y, C и I — общий объем производства, потребления и Инвестируйте соответственно. Здесь мы не рассматриваем концепцию Фридман, проблема самодостаточна Существенно, и уравнение (11.1) является поведением Отравление.
В таком упрощенном виде это предположение не очень реалистично Конечно, это помогает решить проблему. Людмила Фирмаль
Если вы замените выражение (11.1) на (11.2), вы можете сделать следующее: Найдите значение Y в данный момент: в час r ‘= U + TGr + TGr- <V D Первые два члена в правой части уравнения известны любому, кто ранее поверхностно понимал теорию образования Кейнса. Go. Эти условия указывают, что общий уровень дохода зависит Отдельные элементы потребления и инвестиций.
Если объем инвестиций увеличивается на 1, общий доход увеличивается. 1 / (1-P) единица. Это известный аниматор. Также важно отметить, что уровень общего дохода зависит от: Это количество и случайный член в уравнении для функции потребления. Как ты Ты идешь? Предположим, что страна неэкономична в год Потребление увеличилось из-за психических причин.
Давайте делать важные вещи Это событие увеличило общественные и личные расходы. Будет отражено Высокая положительная ценность года благодаря роли Это оценить и захватить такие эффекты. С объемом Такая необычайно высокая стоимость, увеличение потребления за счет выхода Он также увеличивается в соответствии с основным соотношением (11.2). Темпы роста производства Увеличить доход.
Это будет увеличиваться дальше. Потребление по переменной K функции потребления (11.1). как В результате выходной объем увеличивается на ту же величину. прибавление Увеличение производства, и, как следствие, доход снова влияет на объем Расход и т. Д.
Если оно имеет отрицательное значение, последний Эффект похож, только выручка и производство сокращаются. Описанный процесс Если инвестиция изменится, значение множителя будет точным То же: 1 / (1-П). Таким образом, термин (11.3) и появление / (1-р). Если вы поставили себе цель — увеличьте выход Для этого вы можете использовать одинаково хорошо, если вы берете уровень занятости Зарабатывайте деньги с роскошью и инвестициями.
Если тебе все равно Рассказ Тари Б. Мандевиля «Ворчащий улей» (1705) был позднее переиздан. Я рекомендую вам прочитать эту часть «Возможной истории пчелы». Поскольку Y содержит случайные компоненты, А / (1-П) автоматически оказывается соотнесенным со случайными членами Нарушает ном в уравнении (11.1) и четвертое условие Гаусса-Маркова.
При попытке оценить значения A и P с помощью OLS, Оценки смещены, рассчитывается стандартное отклонение Я ошибаюсь Мало что можно сказать о характеристиках малых выборочных оценок. Как оно? Получено из большой выборки и зависит от описательного поведения при изменении Ноа (переменная) модель.
Далее в этой главе Дисперсия переменных и ковариация между переменными в больших выборках Есть некоторые конечные ограничения. Если это предположение выполнено Оценка, полученная с использованием метода наименьших квадратов, является неприемлемой. В рассматриваемой модели большая выборка Var (7) Лимит с /, затем сумма б е + ^. (А.4)
Ошибка оценки не будет равна нулю (для доказательства этого факта, Статья 11.1). 32 С существенными экономическими соображениями, Поскольку 0 <p <1, значение (1-p) является положительным. с того времени ку, значение дисперсии всегда положительно, второй член справа Выражение также будет положительным.
- В результате большой выбор В этой модели значение b (расчетное значение параметра (1) смещено). Up. Величина ошибки зависит от 1) отклонения p от единицы, 2). связь и 2 до a72, то есть от отношения дисперсии случайного члена к дисперсии Эти вложения. Чем больше значение этих двух величин, тем серьезнее Ее проблема. Например, если коэффициент дисперсии ‘/ 4, а значение P = 0,75. В этом случае b 0,75 + 0,25 x (0,25 / 1,25) или 0,80
Проблема смещения, порожденного системой уравнений, Это можно решить, заменив OLS другим методом оценки. В следующем В следующем разделе описаны эти три подхода. Все это методы оценки. Отдельные уравнения, которые обрабатывают каждое уравнение в модели Устанавливается отдельно.
Системный метод с равными параметрами. Людмила Фирмаль
Мнения оцениваются одновременно и в принципе более эффективны, Сделайте их вне рамок этой книги. Что происходит с дисперсией и ковариацией Есть ли у ремня какие-либо конечные ограничения? считать Примеры дисперсии и ковариации с тенденциями в переменных Они растут до бесконечности. В этом случае метод наименьших квадратов, наконец, Юфуку (исследование Дж. Кмента [Kmenta, 1984]).
Простой разбор Если модель, Var (/) растет бесконечно, с большой выборкой МНК не дает ошибок в оценке коэффициентов регрессии Последовательная оценка. Однако даже в этом случае Мы рекомендуем вам использовать альтернативный метод оценки. Наилучшая производительность достигается при небольшом количестве образца. движение 11.1.
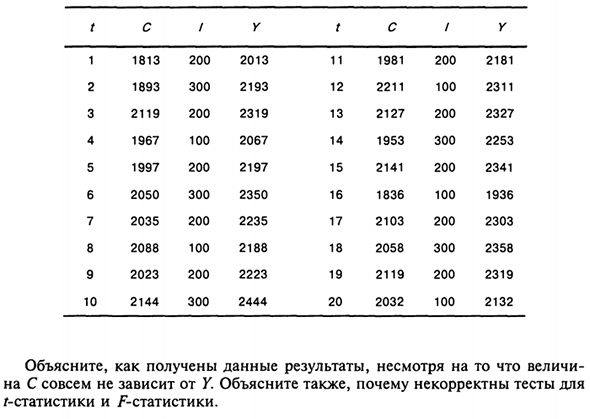
В некоторых сельскохозяйственных странах общее потребление обычно Случайная переменная z добавлена к 2000 единицам, значение равно Из погоды. Среднее значение z = 0, стандартное отклонение -100. заполнитель Суммы инвестиций варьируются в зависимости от четырехлетнего цикла, начиная с 200 лет.
В следующем году увеличится до 300, затем непрерывно уменьшится до 200 и 100, Возврат к 200 и т. Д. Равен сумме общего дохода C и /. Во вкладке Человек представляет данные о значениях C, / и Uza за 20 лет (z Математически ноль нормально распределенная случайная величина Ожидаемое значение и единица времени стандартного отклонения 100).
Традиционные экономисты используют представленные данные для получения: Следующая формула регрессии для зависимости C от Y (в скобках: Стандартное значение ошибки): (? = 512 + 0,68U; L2 = 0,67; (252) (0,11) F = 36,49. Объясните, как эти результаты получены несмотря на следующие факты C полностью независим от Y. Кроме того, / -статистика и ^ -статистика.
Смотрите также:
| Тесты на устойчивость | Структурная и приведенная формы уравнений |
| Метод Бокса—Дженкинса и анализ временных рядов | Косвенный метод наименьших квадратов (КМНК) |
Если вам потребуется помощь по эконометрике вы всегда можете написать мне в whatsapp.

